27. Estadística inferencial: Ajuste de Modelos#

La inferencia busca extraer conclusiones a partir de hechos u observaciones a través de un método o premisa

En el caso particular de la inferencia estadística podemos realizar las siguientes asociaciones

  • Hechos: Datos

  • Premisa: Modelo probabilístico

  • Conclusión: Una cantidad no observada que es interesante

Y lo que buscamos es

Cuantificar la incerteza de la conclusión dado los datos y el modelo

Niveles de la estadística inferencial

La inferencia estadística puede dividirse en los siguientes tres niveles

  1. Ajustar un modelo a nuestros datos

  2. Verificar que el modelo sea confiable

  3. Responder una pregunta usando el modelo

En lo que sigue estudiaremos las herramientas más utilizadas asociadas a cada uno de estos niveles

  1. Estimador de máxima verosimilitud

  2. Bondad de ajuste e Intervalos de confianza

  3. Test de hipótesis

27.1. Estimación de máxima verosimilitud#

En este nivel de inferencia se busca ajustar un modelo teórico sobre nuestros datos. Nos enfocaremos en modelos de tipo parámetrico, es decir aquellos donde se explicita una distribución de probabilidad

Ajustar un modelo que se distribuye \(\mathcal{N}(\mu, \sigma^2)\) a nuestros datos corresponde a

encontrar los valores de \(\mu\) y \(\sigma\) tal que el modelo “se parezca” lo más posible a la distribución empírica de los datos

A continuación definiremos estas nociones

¿Qué distribución ajustar?

Antes de ajustar debemos suponer una distribución. En general podemos ajustar cualquier distribución pero un mal supuesto podría invalidar nuestra inferencia

Consejo

Podemos usar las herramientas de estadística descriptiva para estudiar nuestros datos y tomar esta decisión de manera informada

¿Cómo ajustar mi modelo?

A continuación describiremos un procedimiento para ajustar modelos paramétricos llamado maximum likelihood estimation (MLE)

Sea un conjunto de datos \(\{x_1, x_2, \ldots, x_N\}\). Antes de empezar haremos dos supuestos

  • Supuesto 1: Los datos siguen el modelo \(f(x;\theta)\) donde \(f(\cdot)\) es una distribución y \(\theta\) son sus parámetros

  • Supuesto 2: Las datos son independientes e idénticamente distribuidos (iid)

Usando estos supuestos podemos desarrolar la distribución conjunta de los datos como como

\[\begin{split} \begin{split} f(x_1, x_2, \ldots, x_N |\theta) &= f(x_1|\theta) f(x_2|\theta) \ldots f(x_N|\theta) \\ & = \prod_{i=1}^N f(x_i|\theta) \\ & = \mathcal{L}(\theta) \end{split} \end{split}\]

donde \(\mathcal{L}(\theta)\) se conoce como la verosimilitud o probabilidad inversa de \(\theta\)

Si consideramos que los datos son fijos podemos buscar el valor de \(\theta\) de máxima verosimilitud como

\[\begin{split} \begin{align} \hat \theta &= \text{arg} \max_\theta \mathcal{L}(\theta) \nonumber \\ &= \text{arg} \max_\theta \log \mathcal{L}(\theta) \nonumber \\ &= \text{arg} \max_\theta \sum_{i=1}^N \log f(x_i|\theta) \end{align} \end{split}\]

Nota

El segundo paso es valido por que el argumento máximo de \(g(x)\) y \(\log(g(x))\) son equivalentes (el logaritmo es monoticamente creciente)

Ahora sólo falta encontrar el máximo. Podemos hacerlo

  • Analíticamente, derivando con respecto a \(\theta\) e igualando a cero

  • Usando técnicas de optimización iterativas como gradiente descedente

Ejemplo analítico:

Su profesor quiere medir su peso pero sospecha que su pesa está defectuosa. Para comprobarlo mide su peso \(N\) veces obteniendo un conjunto de observaciones \(\{z_i\}\). ¿Es posible obtener un estimador del peso real \(\hat z\) a partir de estas observaciones?

Podemos modelar las observaciones como

\[ z_i = \hat z + \varepsilon_i \]

donde \(\varepsilon_i\) corresponde al ruido o error del instrumento y asumiremos que \(\varepsilon_i \sim \mathcal{N}(0, \sigma_\varepsilon^2)\), es decir que el ruido es independiente y Gaussiano con media cero y varianza \(\sigma_\varepsilon^2\) conocida

Entonces la distribución de \(z_i\) es

\[ f(z_i|\hat z) = \mathcal{N}(\hat z, \sigma_\varepsilon^2) \]

Para encontrar \(\hat z\), primero escribimos el logaritmo de la verosimilitud

\[\begin{split} \begin{align} \log \mathcal{L}(\hat z) &= \sum_{i=1}^N \log f(z_i|\hat z) \nonumber \\ &= \sum_{i=1}^N \log \frac{1}{\sqrt{2\pi\sigma_\varepsilon^2}} \exp \left ( - \frac{1}{2\sigma_\varepsilon^2} (z_i - \hat z)^2 \right) \nonumber \\ &= -\frac{N}{2}\log(2\pi\sigma_\varepsilon^2) - \frac{1}{2\sigma_\varepsilon^2} \sum_{i=1}^N (z_i - \hat z)^2 \nonumber \end{align} \end{split}\]

Luego debemos resolver

\[\begin{split} \begin{align} \hat \theta &= \text{arg} \max_\theta \log \mathcal{L}(\theta) \nonumber \\ &= \text{arg} \max_\theta - \frac{1}{2\sigma_\varepsilon^2} \sum_{i=1}^N (z_i - \hat z)^2 \end{align} \end{split}\]

donde podemos ignorar el primer término de la verosimilitud ya que no depende de \(\theta\)

Para encontrar el máximo derivamos la expresión anterior e igualamos a cero

\[ -\frac{1}{2\sigma_\varepsilon^2} \sum_{i=1}^N 2(z_i - \hat z) = 0. \]

Finalmente si despejamos llegamos a que

\[ \hat z = \frac{1}{N} \sum_{i=1}^N z_i, \]

que se conoce como el estimador de máxima verosimilitud para la media de una Gaussiana

Nota

Podemos comprobar que es un máximo utilizando la segunda derivada

A continuación veremos como hacer ajuste de parámetros con MLE para distintas distribuciones conocidas utilizando scipy

27.2. Estimación MLE con scipy#

El módulo scipy.stats provee de un gran número de distribuciones teóricas. Los objetos de tipo distribución comparten algunos métodos, entre ellos:

  • pdf/pmf(x): Retorna la función de densidad/masa de probabilidad evaluada en \(x\)

  • cdf(x): Retorna la función de densidad/masa acumulada evaluada en \(x\)

  • ppf(p): Retorna el inverso de la distribución acumulada

  • rvs(size=N): Retorna \(N\) muestras a partir de la distribución

  • fit(data): Retorna los parámetros de la distribución ajutados al arreglo data

Importante

El método fit realiza estimación de máxima verosimilitud para obtener los parámetros

Nota

El método fit sólo está disponible para distribuciones univariadas (continuas o discretas)

Para ejemplificar el uso de fit utilizaremos los siguientes datos

import pickle
import numpy as np
import scipy.stats

with open("data/mistery_data.pkl", "rb") as f:
    mistery_data = pickle.load(f)

Para ajustar un modelo parámetrico a estos datos primero creamos un objeto distribución y luego llamamos su método fit

Por ejemplo si ajustamos una distribución normal a mistery_data obtenemos:

normal_params = scipy.stats.norm.fit(mistery_data)
normal_params

(1.7598526388767328, 0.5437958926009934)

El resultado son los estimadores de máxima verosimilitud de la media y la desviación estándar de la distribución normal

Podemos visualizar el resultado del modelo ajustado utilizando pdf, sobre una objeto distribución creado a partir de los parámetros obtenidos

Observemos el resultado en conjunto a un histograma de mistery_data

fitted_distribution = scipy.stats.norm(*normal_params)

x_eval = np.linspace(0, 4, num=100)
p_eval = fitted_distribution.pdf(x_eval)

%matplotlib inline
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)
ax.hist(mistery_data, density=True, bins=20, label='data', alpha=0.75)
ax.plot(x_eval, p_eval, lw=2, c='k', label='model')
ax.legend();
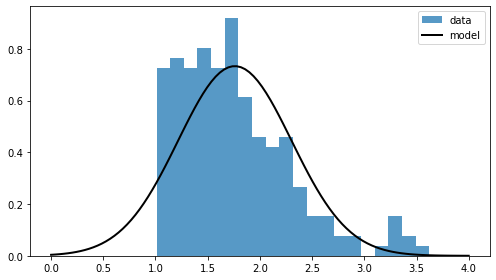
../../_images/01ef1363af297009266eef739060fd0ef7d1f6f3dee4c70f170bb000f9d77beb.png

La visualización revela que los datos tienen una distribución asimétrica (cola derecha más larga)

Ajustar con un modelo normal no fue una buena decisión

Intentemos nuevamente el ajuste pero con distribuciones de cola derecha larga:

fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)
ax.hist(mistery_data, density=True, label='data', alpha=0.75, bins=20)

for dist in [scipy.stats.gamma, 
             scipy.stats.lognorm, 
             scipy.stats.gumbel_r]:
    mle_params = dist.fit(mistery_data)
    print(mle_params)
    ax.plot(x_eval, dist(*mle_params).pdf(x_eval), lw=2, label=dist.name)
    
ax.legend();

(1.790519835925755, 0.9907786403961358, 0.4295227907552)
(0.5432456929387437, 0.7550798666410953, 0.8711472938350178)
(1.5177983118106886, 0.4010033437891445)
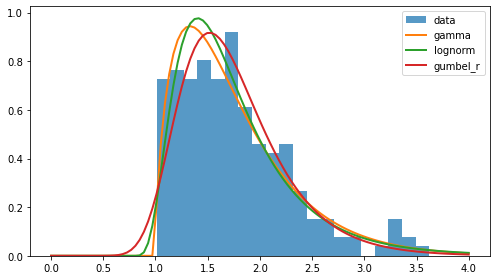
../../_images/a4dfa2a05898e0cce70681d191d2d53fd3f1ac44d55089d8e0cc28af43d5d233.png

A simple vista, el resultado del ajuste es superior al caso normal

¿Cómo decidir cual modelo es superior?

Para eso profundizaremos en el segundo nivel de la estadística inferencial

27.3. Verificación de modelos#

Una vez que hemos ajustado un modelo es buena práctica verificar la calidad o bondad del ajuste. Esto se puede hacer gráficamente utilizando histogramas, gráficos probabilidad-probabilidad (pp plot) o gráficos cuantil-cuantil (qq plot)

Ver también

Para crear qq-plots o pp-plots en Python sugiero la librería statsmodels

También es muy usual visualizar la CDF de nuestro modelo teórico contra la CDF empírica de los datos. Por ejemplo:

def ECDF(data):
    data = np.sort(data)
    n = len(data)
    def result(x):
        return np.searchsorted(data, x, side='right')/n
    return result

fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)

ax.plot(x_eval, ECDF(mistery_data)(x_eval), lw=2, ls='--', label='ECDF')

for dist in [scipy.stats.norm,
             scipy.stats.gamma]:
    mle_params = dist.fit(mistery_data)
    ax.plot(x_eval, dist(*mle_params).cdf(x_eval), lw=2, 
            label=dist.name, alpha=1.)
    
ax.legend();
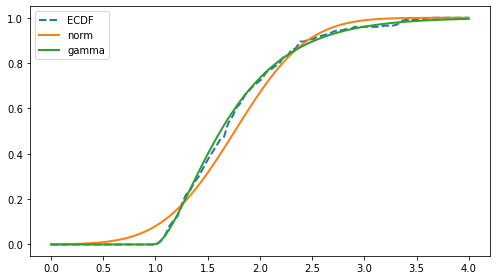
../../_images/1e11d73141f86cb5398c3cb978ec15fb25d576b0742a451b09b95995d935af50.png

Visualmente, el modelo gamma sigue más de cerca a la ECDF que el modelo normal

Test de Kolmogorov-Smirnov

Existen pruebas como el test de Kolmogorov-Smirnov (KS) y el test de Anderson-Darling (AS) que miden la diferencia entre la CDF empírica y teórica

En particular el test de KS se basa en el siguiente estadístico de prueba

\[ D_n = \sup_x |F_n(x) - F(x)|, \]

es decir la distancia absoluta más grande entre \(F_n(x)\), la CDF empírica, y \(F(x)\), una CDF teórica de referencia

Advertencia

El test de KS sólo se puede usar para distribuciones univariadas y continuas

Nota

El test de KS puede usarse para comparar dos muestras o para comparar una muestra con una distribución teórica

El test de KS de una muestra está implementado en scipy.stats.kstest. Los principales argumentos de esta función son

  • un ndarray con las observaciones de nuestra muestra

  • un método cdf de una distribución continua de scipy.stats

La función retorna un objeto cuyo atributo statistic es equivalente a \(D_n\)

A continuación se calcula el valor de \(D_n\) para cuatro distribuciones teóricas contra la CDF empírica de mistery_data:

for dist in [scipy.stats.norm,
             scipy.stats.gamma, 
             scipy.stats.lognorm, 
             scipy.stats.gumbel_r]:
    
    mle_params = dist.fit(mistery_data)
    fitted_distribution = dist(*mle_params)
    result = scipy.stats.kstest(mistery_data, fitted_distribution.cdf)
    print(f"{dist.name:<10}: Dn = {result.statistic:0.4f}")
    

norm      : Dn = 0.0981
gamma     : Dn = 0.0538
lognorm   : Dn = 0.0525
gumbel_r  : Dn = 0.0493

La distribución de menor distancia es “gumbel_r”, sin embargo

¿Es significativa la diferencia en distancia que estamos observando?

Para responder esta pregunta podemos realizar un test de hipótesis. Este es el tema principal de la lección siguiente

Advertencia

scipy.stats.kstest también retorna un p-value asociado a la hipótesis nula de que las distribuciones que se están comparando son iguales. Este p-value sólo es válido si la CDF teórica no fue ajustada con los datos de la CDF empírica, por lo tanto lo hemos ignorado en este ejemplo.

Ver también

  • Para calcular un p-value para el test de KS donde la distribución teórica fue ajustada utilizando MLE la opción es utilizar bootstrap. Lo veremos en una lección futura

  • Para calcular el estadístico de Anderson-Darling (AD) sugiero la librería statsmodels. AD es más sensible que KS cuando la diferencia está concentrada en las colas de la distribución

  • Para variables discretas se puede usar el test \(\chi^2\) de bondad de ajuste