25. Distribuciones de probabilidad

Una distribución de probabilidad es una función que relaciona los valores posibles de una Variable Aleatoria (VA) con sus respectivas probabilidades de ocurrir. En general hacemos la distinción entre

Función de masa de probabilidad (FMP)

Nombre que recibe la distribución de una VA de soporte discreto.

Si \(p_X(x)\) es una PMF entonces \(p_X(x) \in [0, 1] ~\forall x\) y \(\sum_{x} p_X(x) = 1\)

Función de densidad de probabilidad (FDP)

Nombre que recibe la distribución de una VA de soporte continuo.

Si \(f_X(x)\) es una PDF entonces \(f_X(x) \geq 0\) y \(\int f_X(x) \,dx = 1\)

Utilizando la FMP/FDP de una VA podemos calcular la probabilidad de un evento. Por ejemplo, sea una VA discreta \(X\) cuya PMF es \(p_X(\cdot)\). Si \(a\) es parte de su dominio puedo calcular la probabilidad de ocurrencia de \(a\) como

\[ P(X = a) = p_X(a) \]

Sea ahora una VA continua \(Y\) cuya PDF es \(f_Y(\cdot)\). Si \(b\) es parte de su dominio no es posible calcular si probabilidad, pues es infinitesimal. Sin embargo podemos calcular la probabilidad para un rango como

\[ P(a < Y < b) = \int_{a}^{b} f_Y(x) \,dx = F_Y(b) - F_Y(a) \]

donde \(F_Y()\) se conoce como la función de densidad acumulada

25.1. Distribuciones comunes con scipy

El estudio del los fenómenos y procesos aleatorios ha traido consigo el descubrimiento de una gran lista de distribuciones de probabilidad.

La siguiente tabla presenta algunas de las distribuciones más comunes con ejemplos de los fenomenos que buscan modelar

Distribución	Fenómeno que representa	Ejemplo
Bernoulli	Evento binario	Lanzamiento de una moneda
Binomial	Multiples eventos binarios independientes
Categórica	Evento con \(k\) valores posibles	Lanzamiento de un dado, Ruleta
Poisson	Conteo de eventos ocurridos en un período de tiempo	Cantidad de alumnos que llegan entre 9:50 y 10:00
Exponencial	Valor continuo positivo	Tiempo de espera entre eventos
Gamma	Valor continuo positivo	Tiempos de espera hasta que ocurren \(n\) eventos
Beta	Valor continuo en \([0, 1]\)	Tiempo para completar una tarea, proporciones
Normal/Gaussiana	Valor continuo ubicado en la vecindad de un valor central	Demasiados
Uniforme	Valor acotado a un rango, todos con igual probabilidad de ocurrencia

Consejo

Familiarizarse con la forma de estas distribuciones nos facilitará la tarea de proponer modelos para nuestros datos

A continuación utilizaremos scipy para visualizar algunas de estas distribuciones

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats

Una gran número de distribuciones teóricas se encuentran implementadas en el módulo stats de scipy. Los constructores de las distribuciones disponibles se pueden encontrar divididos en tres grupos:

• discretas: Distribuciones univariadas con soporte binario, entero o categórico

• continuas: Distribuciones univariadas con soporte en los números reales

• multivariada

Por ejemplo para crear una distribución Normal/Gaussiana con media cero y desviación estándar uno:

dist = scipy.stats.norm(loc=0, scale=1)
dist

<scipy.stats._distn_infrastructure.rv_frozen at 0x7f75df07b460>

Los objetos de tipo distribución comparten algunos métodos, entre ellos:

• pdf/pmf(x): Retorna la función de densidad/masa de probabilidad evaluada en \(x\)

• cdf(x): Retorna la función de densidad/masa acumulada evaluada en \(x\)

• ppf(p): Retorna el inverso de la distribución acumulada

• rvs(size=100): Retorna \(100\) muestras a partir de la distribución

A continuación vermos algunas FDP/FMP de distribuciones comunes

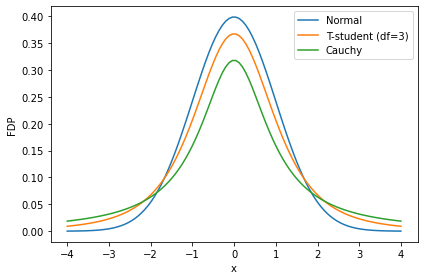
Partiendo por tres distribuciones con soporte en los números reales, la distribución normal, t-student y de Cauchy

x = np.linspace(-4, 4, num=100)
pdf = dist.pdf(x)

fig, ax = plt.subplots(figsize=(6, 4), tight_layout=True)
ax.plot(x, scipy.stats.norm(loc=0, scale=1).pdf(x), label='Normal')
ax.plot(x, scipy.stats.t(df=3, loc=0, scale=1).pdf(x), label='T-student (df=3)')
ax.plot(x, scipy.stats.cauchy(loc=0, scale=1).pdf(x), label='Cauchy')
ax.set_ylabel('FDP')
ax.set_xlabel('x')
ax.legend();

Nota

Las tres distribuciones son simétricas, pero difieren en el comportamiento de sus colas. La distribución de Cauchy tiene las colas más pesadas y la normal las más ligeras

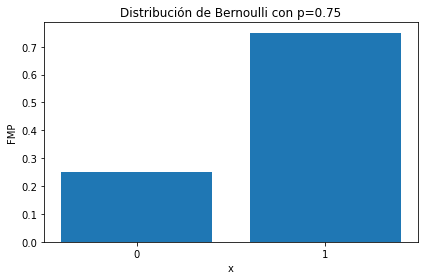
La distribución de Bernoulli tiene soporte binario

dist = scipy.stats.bernoulli(p=0.75)

fig, ax = plt.subplots(figsize=(6, 4), tight_layout=True)
ax.bar([0, 1], dist.pmf([0, 1]))

ax.set_xticks([0, 1])
ax.set_ylabel('FMP')
ax.set_xlabel('x');
ax.set_title(f'Distribución de Bernoulli con p={0.75}');

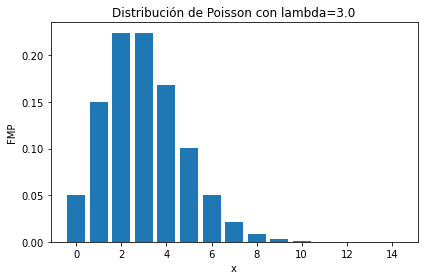
La distribución de Poisson tiene soporte en los números naturales más el cero

x = np.arange(0, 15, step=1)
dist = scipy.stats.poisson(mu=3.)

fig, ax = plt.subplots(figsize=(6, 4), tight_layout=True)
ax.bar(x, dist.pmf(x))
ax.set_ylabel('FMP')
ax.set_xlabel('x');
ax.set_title(f'Distribución de Poisson con lambda={3.}');

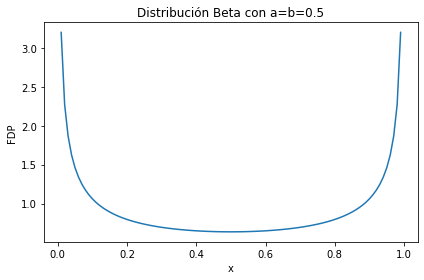
La distribución Beta tiene soporte en el rango \([0, 1]\) de los números reales

x = np.arange(0, 1, step=0.01)
dist = scipy.stats.beta(a=0.5, b=0.5)

fig, ax = plt.subplots(figsize=(6, 4), tight_layout=True)
ax.plot(x, dist.pdf(x))
ax.set_ylabel('FDP')
ax.set_xlabel('x');
ax.set_title(f'Distribución Beta con a=b={0.5}');

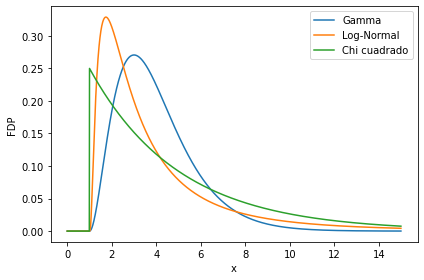
Las distribuciones Gamma, Log-Normal y \(\chi^2\) tienen soporte en los números reales no-negativos

x = np.arange(0, 15, step=0.01)

fig, ax = plt.subplots(figsize=(6, 4), tight_layout=True)
ax.plot(x, scipy.stats.gamma(a=3, loc=1, scale=1).pdf(x), label='Gamma')
ax.plot(x, scipy.stats.lognorm(s=1, loc=1, scale=2).pdf(x), label='Log-Normal')
ax.plot(x, scipy.stats.chi2(df=2, loc=1, scale=2).pdf(x), label='Chi cuadrado')
ax.set_ylabel('FDP')
ax.set_xlabel('x')
ax.legend();

Nota

Cuando una variable \(X\) tiene distribución log-normal significa que \(Y=\log(X)\) se distribuye normal

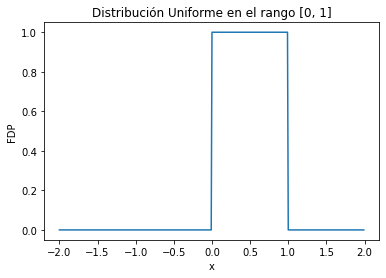
La distribución uniforme tiene rango en los números reales en un rango determinado por sus parámetros

x = np.arange(-2, 2, step=0.01)
dist = scipy.stats.uniform(loc=0, scale=1)

fig, ax = plt.subplots()
ax.plot(x, dist.pdf(x))
ax.set_ylabel('FDP')
ax.set_xlabel('x');
ax.set_title(f'Distribución Uniforme en el rango [0, 1]');

Ver también

El zoológico de distribuciones permite visualizar interactivamente la forma de las distribuciones más comunes

25.2. ¿Por qué la distribución Gaussiana es tan común?

El siguiente sitio web muestra algunos ejemplos de la fenómenos que se distribuyen de forma Gaussiana: https://galtonboard.com/probabilityexamplesinlife

¿Por qué esta distribución parece ser tan común?

Para responder consideremos lo siguiente

Ley de los grandes números

Sean \(X_1, X_2, \ldots, X_N\) V.A independientes e idénticamente distribuidas (iid) con media \(\mu\). Se cumple que su promedio

\[ \bar X = \frac{1}{N} (X_1 + X_2 + \ldots + X_N) \]

tiende a \(\mu\) cuando \(N \to \infty\)

Teorema central del límite

Si \(X_1, X_2, \ldots, X_N\) son V.A iid, entonces su promedio de distribuye como

\[ \bar X \sim \mathcal{N}(\mu, \sigma^2/N) \]

Es decir que

El promedio (o suma) se distribuye normal sin importar la distribución original de las V.A.

siempre y cuando las VA sean independientes. ¿Cúantos de los ejemplos del sitio web mencionado corresponden a sumas o promedios?

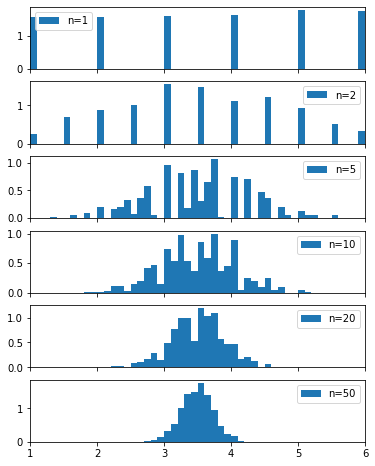
Ejercicio formativo: Sea una variable aleatoria que corresponde al lanzamiento de \(n\) dados de seis caras. Lance los \(n\) dados 1000 veces y muestre con la distribución del promedio de los \(n\) dados. Considere \(n=1, 2, 5, 10, 20, 50\)

La distribución multinomial modela la ocurrencia de \(n\) eventos cada uno con \(k\) categorías. Se considera como una generalización de la distribución categórica (\(n=1\)) y de la binomial (\(k=2\))

fig, ax = plt.subplots(6, figsize=(6, 8), sharex=True)
for n, ax_ in zip([1, 2, 5, 10, 20, 50], ax):
    dist = scipy.stats.multinomial(n=n, p=[1/6]*6)
    repeats = dist.rvs(size=1000)
    average_dice = np.sum(repeats*range(1, 7)/n, axis=1)
    ax_.hist(average_dice, bins=60, density=True, range=(0, 6), label=f"n={n}")
    ax_.legend()
ax_.set_xlim([1, 6]);

Importante

A medida que \(n\) crece la distribución del promedio tiende a una normal, tal como lo predice el teorema central del límite

Para mostrar las distribuciones se utilizó una herramienta gráfica llamada histograma. En la siguiente lección aprenderemos sobre ella