18. Operaciones sobre ndarrays#
import numpy as np
18.1. Operaciones aritméticas y Broadcasting#
Los ndarray soportan las operaciones aritméticas básicas
Suma: +, +=
Resta: -, -=
Multiplicación: ,=
División: /, /=
División entera: //, //=
Exponenciación: ** , **=
Estas operaciones tienen un comportamiento element-wise (elemento a elemento), es decir
Veamos algunos ejemplos:
N = 3
A = np.eye(N)
B = np.ones(shape=(N, N))
A, B
(array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]]),
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]]))
A + B
array([[2., 1., 1.],
[1., 2., 1.],
[1., 1., 2.]])
A*B
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
Nota
El operador * no corresponde a la multiplicación de matrices sino a la multiplicación elemento por elemento
Broadcasting
Cuando los ndarray que estamos operando no son del mismo tamaño se hace un broadcast
Por ejemplo si operamos una constante con un arreglo, la constante se opera con cada elemento del arreglo
A - 1
array([[ 0., -1., -1.],
[-1., 0., -1.],
[-1., -1., 0.]])
Las siguientes son las reglas automáticas de broadcasting
Si dos arreglos son de dimensiones distintas la dimensión del más pequeño se agranda con «1»s por la izquierda
Si dos arreglos tienen tamaños ditintos, el que tiene tamaño “1” se estira en dicha dimensión
Si en cualquier dimensión los tamaños son distintos y ninguno es igual a “1” ocurre un error
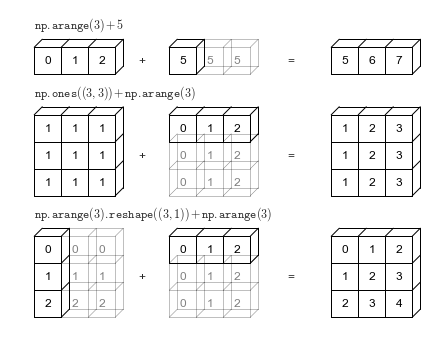
Imagen tomada del Python Data Science Handbook
Observe los siguientes ejemplos y reflexione sobre las reglas de broadcast que se está aplicando en cada caso
C = np.arange(N)
B = np.ones(shape=(N, N))
C, B
(array([0, 1, 2]),
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]]))
B+C
array([[1., 2., 3.],
[1., 2., 3.],
[1., 2., 3.]])
B + C.reshape(-1, 1)
array([[1., 1., 1.],
[2., 2., 2.],
[3., 3., 3.]])
C.reshape(1, N) + C.reshape(N, 1)
array([[0, 1, 2],
[1, 2, 3],
[2, 3, 4]])
Operaciones matriciales
Antes dijimos que la multiplicación con * se realiza elemento a elemento
Para realizar una multiplicación matricial propiamente tal podemos usar dot o el operador @
A = np.arange(4).reshape(2, 2)
B = np.arange(4)[::-1].reshape(2, 2)
A, B
(array([[0, 1],
[2, 3]]),
array([[3, 2],
[1, 0]]))
Note la diferencia:
A*B
array([[0, 2],
[2, 0]])
np.dot(A, B)
array([[1, 0],
[9, 4]])
Otras operaciones matricionales útiles son:
np.innerque calcula el producto escalar o producto internonp.outerque calcula el producto externonp.crossque calcula cruz
El módulo linalg de NumPy contiene muchas más funciones de álgebra lineal que nos permiten
Calcular matriz inversa, determinantes y trazas
Resolver sistemas lineales
Factorizar matrices
Calcular valores y vectores propios
entre otros. Este módulo será estudiando en una lección siguiente
18.2. Operaciones de reducción#
Una reducción es una operación que agrega los valores de un arreglo entregando un único valor como respuesta
La reducción más básica es la suma agregada
Algunas de las reducciones disponibles en NumPy son:
sum,prodamax,amin,argmax,argminmean,std,var,percentile,mediancumsum,cumprod
Nota
Las reducciones pueden realizar al ndarray completo o a un subconjunto de sus ejes
Diferencia entre sumar en el eje de filas, columnas y suma total:
A = np.tile(np.arange(3), (2, 1))
A
array([[0, 1, 2],
[0, 1, 2]])
np.sum(A, axis=0)
array([0, 2, 4])
np.sum(A, axis=1)
array([3, 3])
np.sum(A)
6
Encontrar el valor y posición del máximo en un arreglo es también un tipo de reducción
A = np.random.randn(2, 3)
A
array([[ 0.13159486, 1.22272348, 0.48631899],
[-0.04709683, -0.49368269, 0.40754107]])
np.amax(A, axis=0) # El valor del máximo en el eje 0
array([0.13159486, 1.22272348, 0.48631899])
np.argmax(A, axis=0) # La posición del máximo en el eje 0
array([0, 0, 0])
Las operaciones de reducción de NumPy son altamente eficientes
Hagamos una pequeña prueba de desempeño sumando un vector
Usaremos la magia de IPython @timeit que nos permite medir tiempo de cómputo
A = np.arange(100000)
def suma_loop(arreglo):
suma = 0.
for elemento in arreglo:
suma += elemento
return suma
L = list(A)
%timeit -n10 suma_loop(A)
%timeit -n10 suma_loop(L)
%timeit -n10 sum(A)
%timeit -n10 sum(L)
%timeit -n10 np.sum(L)
%timeit -n10 np.sum(A)
23.1 ms ± 998 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
16.8 ms ± 222 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
10.6 ms ± 220 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
7.22 ms ± 94.3 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
6.52 ms ± 113 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
115 µs ± 11.7 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
Y el resultado es por supuesto el mismo
np.allclose(np.sum(A), sum(L))
True
Muchas de las funciones de reducción cuentan con versiones seguras contra NaNs
Por ejemplo si sumamos el siguiente arreglo:
A = np.array([1., 10., 2., np.nan])
np.sum(A)
nan
En cambio si utilizamos nansum:
np.nansum(A)
13.0
Si queremos encontrar los NaN en un arreglo podemos usar isnan que devuelve una máscara booleana con True donde habían NaNs
np.isnan(A)
array([False, False, False, True])
Podemos usar esta máscara para eliminar los elementos invalidos del arreglo
A[~np.isnan(A)]
array([ 1., 10., 2.])
18.3. Operaciones vectorizadas#
Las operaciones vectorizados son funciones que operan elemento a elemento (element-wise)
Ya vimos las operaciones aritméticas elemento a elemento pero existen muchas más
Por ejemplo para calcular el valor absoluto de los elementos de un arreglo
A = np.random.randn(2, 3)
A
array([[ 0.31191169, -0.53796815, -0.29957235],
[-0.39255606, -0.38035686, -0.5326143 ]])
np.absolute(A) # Equivalente a np.abs(A)
array([[0.31191169, 0.53796815, 0.29957235],
[0.39255606, 0.38035686, 0.5326143 ]])
Exponenciar un arreglo
x = np.arange(5)
np.power(x, 2) # Equivalente a x**2
array([ 0, 1, 4, 9, 16])
np.sqrt(x)
array([0. , 1. , 1.41421356, 1.73205081, 2. ])
Calcular funciones exponencial, logaritmo y trigonométricas a partir de una arreglo
x = np.array([0.1, 1., 10.0])
np.log(x) # También está log2, log10
array([-2.30258509, 0. , 2.30258509])
np.exp(x)
array([1.10517092e+00, 2.71828183e+00, 2.20264658e+04])
np.sin(x), np.cos(x), np.tan(x)
(array([ 0.09983342, 0.84147098, -0.54402111]),
array([ 0.99500417, 0.54030231, -0.83907153]),
array([0.10033467, 1.55740772, 0.64836083]))
También existe las versiones
hiperbólicas:
sinh,cosh,tanhinversas:
arcsin,arccosyarctan
Otras funciones útiles:
El signo de cada elemento de x:
sign(x)Uno dividido los elementos de x :
reciprocal(x)Redondeno hacia abajo o hacia arriba:
round(x),floor(x)yciel(x)Parte real o imaginaria de un número complejo y:
real(y),imag(y)Conjugado de un número complejo:
conj(y),
18.3.1. Operaciones booleanas#
NumPy soporta operaciones booleanas sobre ndarray
A = np.arange(6).reshape(2, 3)
A
array([[0, 1, 2],
[3, 4, 5]])
A == 4 # Es un alias de np.equal(A, 4)
array([[False, False, False],
[False, True, False]])
Podemos crear una máscara booleana para indexar un arreglo (fancy indexing)
mask = ~(A % 2 == 0) & (A > 2)
mask
array([[False, False, False],
[ True, False, True]])
A[mask]
array([3, 5])
La función where sirve para recuperar el índice de los elementos que cumplen una cierta condición
(ixs, iys) = np.where(~(A % 2 == 0) & (A > 2))
for i, j in zip(ixs, iys):
display("Fila {0} Columna {1} Valor {2}".format(i, j, A[i, j]))
'Fila 1 Columna 0 Valor 3'
'Fila 1 Columna 2 Valor 5'
Otras funciones útiles
any(x)Para comprobar si al menos un elemento de x esTrueall(x): Para comprobar si todos los elementos de x sonTrue
x = np.random.randn(2, 3)
x
array([[-1.15844041, 0.06928647, -0.3419704 ],
[-0.36894413, -0.07347014, 0.69646578]])
b = (x > 0) & (x**2 > 0.5)
b
array([[False, False, False],
[False, False, False]])
np.any(b)
False
np.all(b)
False
18.4. Operaciónes de conjuntos#
Operaciones de tipo union, intersección y diferencia entre arreglos 1D
Si se les entrega un arreglo de mayor dimensión este se aplanará automaticamente
A = np.arange(6)
B = np.array([0, 1, 10, 100])
A, B
(array([0, 1, 2, 3, 4, 5]), array([ 0, 1, 10, 100]))
La unión e intersección, respectivamente:
np.union1d(A, B)
array([ 0, 1, 2, 3, 4, 5, 10, 100])
np.intersect1d(A, B)
array([0, 1])
O los elementos que existen a A y no en B (y viceversa)
np.setdiff1d(A, B)
array([2, 3, 4, 5])
np.setdiff1d(B, A)
array([ 10, 100])
18.5. Operaciones de ordenamiento#
NumPy provee la función np.sort para ordernar un ndarray
Se puede usar el argumento kind para escoger distintos algoritmos de ordenamiento (por defecto quicksort)
El argumento axis especifica que eje se va a ordenar
A = np.random.randn(2, 2)
A
array([[ 0.71298521, -0.45263446],
[-0.05345455, 1.78528422]])
np.sort(A, axis=1)
array([[-0.45263446, 0.71298521],
[-0.05345455, 1.78528422]])
np.sort(A, axis=0)
array([[-0.05345455, -0.45263446],
[ 0.71298521, 1.78528422]])
np.sort(A, axis=None) # Ordena el arreglo aplanado con ravel
array([-0.45263446, -0.05345455, 0.71298521, 1.78528422])
La función np.argsort entrega un arreglo de índices que ordena el arreglo de menor a mayor
A = np.array(["A", "B", "C"])
B = np.array([2, 4, 1])
A, B
(array(['A', 'B', 'C'], dtype='<U1'), array([2, 4, 1]))
idx = np.argsort(B)
idx
array([2, 0, 1])
A[idx]
array(['C', 'A', 'B'], dtype='<U1')