20. Resolviendo sistemas de ecuaciones lineales#

En su forma más general un sistema de ecuaciones lineales se ve como

\[\begin{split} \begin{align} A_{11} x_{1} + A_{12} x_{2} + \ldots + A_{1M} x_M &= b_1 \nonumber \\ A_{21} x_{1} + A_{22} x_{2} + \ldots + A_{2M} x_M &= b_2 \nonumber \\ &\vdots \nonumber \\ A_{N1} x_{1} + A_{N2} x_{2} + \ldots + A_{NM} x_M &= b_N \nonumber \\ \end{align} \end{split}\]

donde

  • \(A_{ij}\) y \(b_i\) son los coeficientes del sistema

  • \(N\) es la cantidad de ecuaciones del sistema

  • \(M\) es la cantidad de incógnitas del sistema

El sistema anterior puede escribirse de forma matricial como

\[ A x = b \]

donde \(A \in \mathbb{R}^{N \times M}\) y \(b \in \mathbb{R}^N\)

Revisemos a continuación como se resuelven problemas de este tipo utilizando scipy.linalg

%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import scipy.linalg

20.1. Solución de un sistema cuadrado#

Este es un caso particular donde la matriz \(A\) tiene igual número de filas y columnas (\(N=M\))

Asumiendo que la inversa de \(A\) existe podemos resolver este sistema como

\[\begin{split} \begin{align} A x &= b \nonumber \\ A^{-1} A x &= A^{-1} b \nonumber \\ x &= A^{-1} b \nonumber \end{align} \end{split}\]

donde \(A A^{-1} = I\)

A continuación veremos como calcular la inversa de una matriz y resolver el sistema de ecuaciones cuadrado

Ejemplo Sea el sistema de tres ecuaciones y tres incognitas

\[\begin{split} \begin{align} x_1 - 2x_2 + 3x_3 &= 4 \\ 2x_1 - 5x2 + 12x_3 &= 15 \\ 2x_2 - 10x_3 &= -10 \end{align} \end{split}\]

que podemos reescribir como

\[\begin{split} \begin{pmatrix} 1 & -2 & 3 \\ 2 & -5 & 12 \\ 0 & 2 & -10 \end{pmatrix} \cdot \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 4 \\ 15 \\ -10 \end{pmatrix} \end{split}\]

de donde es directo identificar \(A\) y \(b\)

A = np.array([[1, -2, 3], [2, -5, 12], [0, 2, -10]])
b = np.array([4, 15, -10])

Dado que \(A\) es una matriz cuadrada podemos intentar invertla la función inv

Ainv = scipy.linalg.inv(A)
Ainv

array([[-13. ,   7. ,   4.5],
       [-10. ,   5. ,   3. ],
       [ -2. ,   1. ,   0.5]])

Con la inversa podemos resolver el problema con

np.dot(Ainv, b)

array([8., 5., 2.])

Nota

Si \(A\) hubiera sido singular, es decir no invertible, la función inv hubiera retornado un LinAlgError

Podemos verificar la invertibilidad de la matriz comprobando que su determinante sea distinto de cero

scipy.linalg.det(A)

-1.9999999999999976

Otra forma de verificar si una matriz es invertible es comprobar que todas sus columnas sean linealmente independientes (LI)

Esto es equivalente a que su rango sea igual al número de columnas, lo cual se puede verificar con la función de NumPy

np.linalg.matrix_rank(A) == A.shape[1]

True

Resolviendo sistemas cuadrados eficientemente

En general si sólo nos interesa \(x\), podemos no realizar el cálculo explícito de \(A^{-1}\). Si un sistema de ecuaciones es grande es preferible no calcular la inversa de \(A\) debido al alto costo computacional necesario

Podemos encontrar \(x\) directamente en un sistema cuadrado usando la función solve

scipy.linalg.solve(A, b)

array([8., 5., 2.])

El resultado es idéntico al anterior

Veamos ahora la diferencia en eficiencia utilizando un sistema más grande

N = 2000
A_big = np.random.rand(N, N) # Matriz cuadrada
b_big = np.random.rand(N, 1) # Vector
%timeit -r5 -n5 np.dot(scipy.linalg.inv(A_big), b_big)
%timeit -r5 -n5 scipy.linalg.solve(A_big, b_big)

297 ms ± 15.7 ms per loop (mean ± std. dev. of 5 runs, 5 loops each)
193 ms ± 11.6 ms per loop (mean ± std. dev. of 5 runs, 5 loops each)

np.allclose(scipy.linalg.solve(A_big, b_big), np.dot(scipy.linalg.inv(A_big), b_big))

True

Usar solve toma un poco más de la mitad del tiempo de utilizar inv+dot

¿Cómo puede ser posible esto?

La respuesta es que solve realiza internamente una factorización del tipo

\[\begin{split} \begin{align} A x &= b \nonumber \\ LU x &= b \nonumber \\ L z &= b \nonumber \end{align} \end{split}\]

Donde \(L\) es una matriz triangular inferior (lower) y \(U\) es una matriz triangular superior (upper)

\[\begin{split} L = \begin{pmatrix} l_{11} & 0 & 0 & \ldots & 0 & 0 \\ l_{21} & l_{22} & 0 &\ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ l_{N1} & l_{N2} & l_{N3} & \ldots & l_{N(N-1)} & l_{NN} \\ \end{pmatrix} \quad U = \begin{pmatrix} u_{11} & u_{11} & u_{13} & \ldots & u_{1(N-1)} & u_{1N} \\ u_{21} & u_{22} & u_{32} &\ldots & u_{2(N-1)} & 0 \\ \vdots & \vdots & \vdots &\ldots & \ddots & \vdots \\ u_{N1} & 0 & 0 & \ldots & 0 & 0\\ \end{pmatrix} \end{split}\]

Luego \(z\) se puede obtener recursivamente

\[ z_1 = \frac{b_1}{l_{11}} \]
\[ z_2 = \frac{b_2 - l_{21} z_1}{l_{22}} \]
\[ z_i = \frac{b_i - \sum_{j=1}^{i-1} l_{ij} z_j}{l_{ii}} \]

y \(x\) se puede obtener recursivamente de \(z\)

En caso de necesitar los factores LU podemos realizar la factorización en scipy con linalg.lu

P, L, U = scipy.linalg.lu(A)
L, U

(array([[1.  , 0.  , 0.  ],
        [0.  , 1.  , 0.  ],
        [0.5 , 0.25, 1.  ]]),
 array([[  2. ,  -5. ,  12. ],
        [  0. ,   2. , -10. ],
        [  0. ,   0. ,  -0.5]]))

20.2. Solución de un sistema rectangular#

Consideremos que

  • Las incógnitas de un sistema representan sus grados de libertad

  • Las ecuaciones de un sistema representan sus restricciones

Si tenemos un sistema

  • con más ecuaciones que incógnitas (\(N>M\)): el sistema está sobredeterminado

  • con más incógnitas que ecuaciones (\(M>N\)): el sistema está infradeterminado

Advertencia

En ambos casos la matriz \(A\) ya no es cuadrada, es decir ya no podemos calcular la inversa

Sin embargo podemos utilizar otros métodos, como mostraremos a continuación

Caso N>M

Sea el vector de error \(e = Ax - b\) de un sistema con más ecuaciones que incognitas.

Podemos encontrar una solución aproximada minimizando la norma euclidiana del error

\[\begin{split} \begin{align} \hat x &= \min_x \|e\|_2^2 \nonumber \\ & = \min_x e^T e \nonumber \\ & = \min_x (Ax -b)^T (Ax -b) \nonumber \\ \end{align} \end{split}\]

Lo cual se conoce como el Problema de mínimos cuadrados

Para continuar tomamos la última expresión y derivamos con respecto a \(x\)

\[\begin{split} \begin{align} \frac{d}{dx} (A x - b)^T (A x -b) &= 2 A^T (A x -b) \nonumber \\ &= 2A^T A x - 2A^T b = 0 \nonumber \\ \rightarrow \hat x &= (A^T A)^{-1} A^T b \nonumber \\ &= A^{\dagger} b \nonumber \\ \end{align} \end{split}\]

donde \(A^{\dagger} = (A^T A)^{-1} A^T\) se conoce como la pseudo-inversa de Moore-Penrose

Caso M>N

La consecuencia de que el sistema sea infradeterminado es que \(A^T A\) no es invertible.

Para resolver el problema infradeterminado se debe agregar una restricción adicional. La más típica es que el vector solución tenga norma mínima, por ejemplo

\[ \min_\theta \| x \|_2^2 ~\text{s.a.}~ Ax =b \]

que se resuelve usando \(M\) multiplicadores de Lagrange \(\lambda\) como sigue

\[\begin{split} \begin{align} \frac{d}{dx} \| x\|_2^2 + \lambda^T (b - Ax) &= 2x - \lambda^T A \nonumber \\ &= 2Ax - A A^T \lambda \nonumber \\ &= 2b - A A^T \lambda = 0 \end{align} \end{split}\]

De donde obtenemos que

\[ \lambda = 2(AA^T)^{-1}b \]

y por lo tanto

\[ \hat x = \frac{1}{2} A^T \lambda = A^T (A A^T)^{-1} b, \]

donde \(A^T (A A^T)^{-1}\) se conoce como la pseudo-inversa “por la derecha”

Resolviendo el sistema rectangular con Python

Sea un sistema de ecuaciones lineales con \(N\neq M\). Podemos usar scipy para

Si \(N>M\) se utiliza la pseudoinversa por la izquierda y la solución de mínimos cuadrados. En cambio si \(M>N\) se utiliza la pseudoinversa para la derecha y la solución de multiplicadores de Lagrange

Ejemplo: Sea el siguiente set de datos de un estudio realizado en los años 50

Referencia: A handbook of small datasets

df = pd.read_csv('data/helados.csv', index_col=0)
df.head()
cons income price temp
1 0.386 78 0.270 41
2 0.374 79 0.282 56
3 0.393 81 0.277 63
4 0.425 80 0.280 68
5 0.406 76 0.272 69

donde cada fila corresponde a un día las columnas corresponde a

  • consumo de helados promedio (pintas per capita)

  • ingreso familiar promedio (dolares)

  • temperatura promedio (grados Fahrenheit)

  • precio promedio de los helados (dolares)

Ahora consideremos la siguiente pregunta

¿Está el consumo de helados influenciado por la temperatura?

Intentemos responder esta pregunta en base al siguiente modelo

\[ \text{cons} = \theta_0 + \theta_1 \cdot \text{temp} \]

que corresponde a un sistema de ecuaciones lineales de dos incognitas y

f"{len(df)} ecuaciones"

'30 ecuaciones'

Es decir que es un sistema sobredeterminado

\[\begin{split} \begin{pmatrix} cons[0] \\ cons[1] \\ \vdots \\ cons[{29}] \end{pmatrix} = \begin{pmatrix} 1&temp[0] \\ 1&temp[1] \\ \vdots & \vdots \\ 1 & temp[29] \end{pmatrix} \begin{pmatrix} \theta_0 \\ \theta_1 \end{pmatrix} \end{split}\]

que podemos resolver utilizando lstsq

A = np.ones(shape=(len(df), 2))
A[:, 1] = df["temp"].values
b = df["cons"].values

theta, residuals, rank, s = scipy.linalg.lstsq(A, b)
theta

array([0.20686215, 0.00310736])

La tupla retornada contiene

  • theta: El resultado buscado

  • residuals: La norma del error al cuadrado

  • rank: El rango de \(A\)

  • s: Los valores singulares de \(A\)

Analicemos gráficamente la solución obtenida

fig, ax = plt.subplots(tight_layout=True)
ax.scatter(df["temp"], df["cons"], s=5, c='k', label='observaciones')
ax.set_xlabel('Temperatura [F]')
ax.set_ylabel('Consumo promedio')
temp_modelo = np.linspace(df["temp"].min(), df["temp"].max(), num=200)
cons_modelo = temp_modelo*theta[1] + theta[0]
ax.plot(temp_modelo, cons_modelo, label='modelo')
ax.legend();
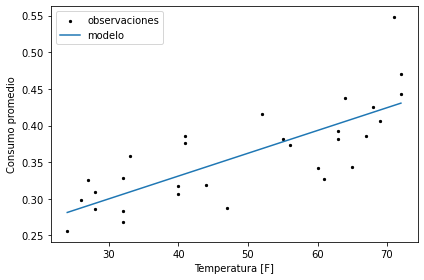
../../_images/50078fd00848982d2e385660a9072be0534a7dd8c7649ba1761cc2e291d7b3d5.png

De donde podemos observar que el consumo promedio tiende al alza con la temperatura promedio

Nota

Lo que acabamos de resolver es un problema conocido como regresión lineal. Más adelante veremos una forma más general de este problema

20.3. Análisis de errores y condition number#

Incluso aunque una matriz sea matemáticamente invertible (determinante distinto de cero), podríamos no ser capaces de resolver el problema numéricamente

Imaginemos una pequeña variación en \(b\) denominada \(\delta b\). Esta variación provoca a su vez una pequeña variación en \(x\) denominada \(\delta x\)

Se puede encontrar una cota que compara el error relativo de \(b\) y \(x\) como

\[ \frac{\| \delta x \|}{\|x\|} \leq \frac{\| A^{-1} \| \|\delta b\|}{\|x\|} = \|A^{-1}\| \|A\| \frac{\| \delta b \|}{\|b\|} \]

donde se usó que \(A \delta x = \delta b\) (propiedad de linealidad)

Nota

Esto significa que un pequeño error relativo en \(b\) puede causar un gran error en \(x\)

El estimador de \(\|A^{-1}\| \|A\|\) es lo que se conoce como condition number

Un sistema se dice “bien condicionado” si este valor es cercano a \(1\) y “mal condicionado” si es mucho mayor que \(1\).

Podemos calcular el condition number con la función de NumPy cond como se muestra a continuación

np.linalg.cond(x, # Arreglo multidimensional
               p # El orden de la norma: 1, 2, 'fro',...
              )