34. Evaluando un clasificador#
A continuación veremos como evaluar de manera cuantitativa el desempeño de un modelo clasificador.
34.1. Matriz de confusión#
Una matriz o tabla de confusión se construye contando los casos que tienen etiqueta real igual a \(i\) y etiqueta predicha igual a \(j\) para \(i \wedge j=1,2,\ldots,C\) donde \(C\) es el número de clases.
La siguiente imagen muestra una matriz de confusión para un problema de \(10\) clases:
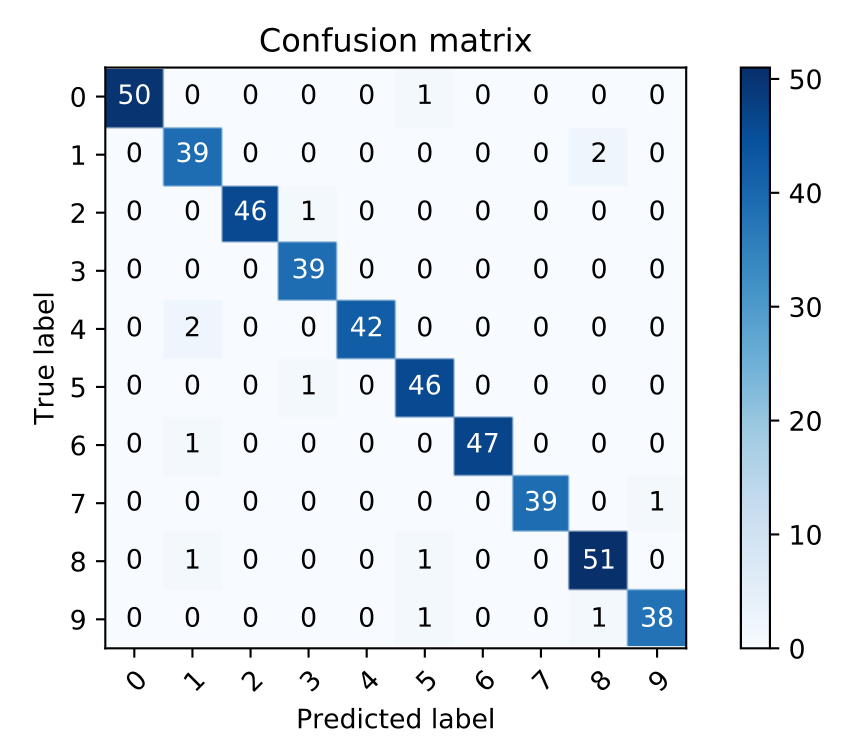
En una matriz de confusión:
los elementos de la diagonal representan las clasificaciones correctas
los elementos fuera de la diagonal representan las clasificaciones erroneas
las filas corresponden a las clases reales
las columnas corresponden a las clases predichas por el clasificador
Ejemplo: En la imagen anterior tenemos \(2\) ejemplos de clase “4” que fueron clasificados como clase “1” por el modelo
En scikit-learn podemos calcular la matriz de confusión usando el módulo sklearn.metrics. Como ejemplo utilizaremos nuevamente un clasificador sobre la base de datos de Cancer.
La función score del clasificador retorna el valor de una métrica llamada accuracy que corresponde a la proporción de casos bien clasificados divido por el total.
from sklearn.datasets import load_breast_cancer
from sklearn.naive_bayes import GaussianNB
data = load_breast_cancer()
X, y, X_names, y_names = data['data'], data['target'], data['feature_names'], data['target_names']
clf = GaussianNB()
clf.fit(X, y)
clf.score(X, y)
0.9420035149384886
Veamos ahora la matriz de confusión.
Nota
La matriz de confusión requiere una etiqueta categórica, es decir no acepta probabilidades. Podemos convertir probabilidades en etiquetas categóricas usando np.argmax(probs, axis=1). También podemos usar el método predict para obtener la predicción categórica directamente.
from sklearn.metrics import confusion_matrix
yhat = clf.predict(X)
cm = confusion_matrix(y, # Etiqueta real
yhat # Etiqueta predicha
)
print(cm)
[[189 23]
[ 10 347]]
También podemos usar el objeto ConfusionMatrixDisplay con sus métodos from_estimator o from_prediction si deseamos producir una matriz de confusión como una figura de matplotlib
%matplotlib inline
from matplotlib import pyplot as plt
from sklearn.metrics import ConfusionMatrixDisplay
fig, ax = plt.subplots(figsize=(5, 4), tight_layout=True)
ConfusionMatrixDisplay.from_estimator(clf, X, y, ax=ax,
display_labels=y_names, #Nombres de las clases
cmap=plt.cm.Blues, # Escala de colores
normalize=None #Permite escoger entre cantidades y porcentajes
);
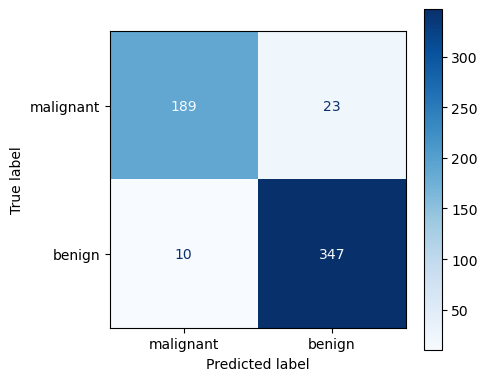
Intepretación:
Hay 10 casos predichos como maligno que en realidad eran benignos: Falso positivo
Hay 23 casos predichos como benignos que en realidad eran malignos: Falso negativo
34.2. Curvas de desempeño#
La matriz de confusión y la exactitud son métricas que depende de un umbral de clasificación o punto de operación particular.
En problemas de clasificación binaria es mucho más informativo medir el desempeño utilizando curvas Receiver operating characteristic (ROC). Una curva ROC es la tasa de verdaderos positivos
en función de la tasa de falsos positivos
para distintos umbrales de clasificación \(R\).
Podemos obtenerla de forma simple utilizando sklearn.metrics.roc_curve
import numpy as np
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y, clf.predict_proba(X)[:, 1])
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(fpr, tpr)
ax.plot([0, 0, 1], [0, 1, 1], 'k--', alpha=0.5)
ax.set_xlabel('Tasa de falsos positivos')
ax.set_ylabel('Tasa de verdaderos positivos');
idx = np.where(fpr < 0.01)[0][-1]
print(f"{fpr[idx]:0.4f}, {tpr[idx]:0.4f}, {thresholds[idx]:0.9f}")
ax.scatter(fpr[idx], tpr[idx], s=50, c='k');
0.0094, 0.8123, 0.999999998
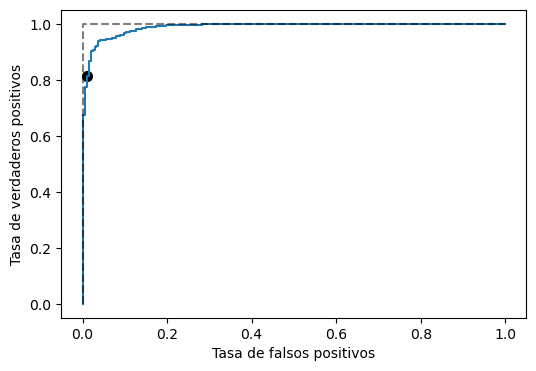
El modelo es mejor mientras más apegada esté la curva azul al punto TPR=1 y FPR=0 (línea punteada negra).
La curva ROC nos permite estudiar todos los puntos de operación a la vez y seleccionar aquel que sea más adecuado para la tarea particular.
De la curva anterior podemos extraer que si el FPR máximo tolerable fuese \(1\)% se alcanzaría una TPR de \(81.23\)%. Además dicho punto de operación corresponde al umbral \(0.999999998\)
34.3. Capacidad de generalización#
¿Cómo podemos saber si el modelo funcionará correctamente en nuevos datos?
La anterior es una pregunta fundamental en aprendizaje de máquinas. Lo que se requiere es poder evaluar la capacidad de generalización del modelo, lo cual es un desafío importante en modelos más complejos.
Ver también
Puedes leer sobre estos temas en el siguiente aquí: https://phuijse.github.io/MachineLearningBook/contents/supervised_learning/validation.html