28. Test de hipótesis#

Supongamos que existe una nueva y contagiosa enfermedad y que se inventa un nuevo tratamiento médico con el fin de erradicarla. A modo de prueba el tratamiento es aplicado a una muestra de la población.

Podemos definir \(X\), una variable aleatoria binaria que indica si el tratamiento fue efectivo o no

En base a estos resultados, ¿cómo concluir formalmente que el tratamiento fue efectivo? además ¿qué podemos decir sobre la efectividad del tratamiento en la población general?

En estadística este tipo de preguntas se resuelven utilizando un test de hipótesis

Test de hipótesis

Es un procedimiento de estadística inferencial para comprobar si el resultado de un experimento es significativo

El primer paso es formular las

Hipótesis

Conjetura que planteamos respecto al resultado de nuestro experimento

Y en general lo que se plantea es una

Hipótesis nula

Es una conjetura que suele representar el “status quo”, es decir el escenario en que los resultados del experimento no son significativos. Se denota como \(H_0\)

La hipótesis nula suele redactarse de las siguientes formas

  • “No hay diferencia entre la muestra X y la muestra Y”

  • “No existe relación entre la variable X y la variable Y”

Para el ejemplo anterior podríamos redactar “No hay diferencia entre los pacientes que tomaron y los que no tomaron el tratamiento”

Importante

El test de hipótesis se diseña para medir que tan fuerte es la evidencia en contra de la hipótesis nula

Ver también

Puedes revisar otros ejemplos más pintorescos de hipótesis nula en este link

El test de hipótesis también considera el complemento (contrario) de la hipótesis nula, que se denomina: hipótesis alternativa, que denotaremos \(H_A\)

28.1. Algoritmo general de un test de hipótesis#

El siguiente es el algoritmo general de un test de hipótesis paramétrico

  1. Definir \(H_0\) y \(H_A\)

  2. Definir un estadístico \(T\)

  3. Obtener la distribución para \(T\) dado que \(H_0\) es cierto

  4. Seleccionar un nivel de significancia \(\alpha\)

  5. Calcular el valor de \(T\) para nuestros datos: \(T_{data}\)

  6. Calcular el p-value

Finalmente:

if \(p < \alpha\) : se rechaza la hipótesis nula con confianza (1-\(\alpha\))

else: No hay suficiente evidencia para rechazar la hipótesis nula

Nota

El valor de \(\alpha\) nos permite controlar el Error tipo I, es decir el error que cometemos si rechazamos \(H_0\) cuando en realidad era cierta (falso positivo). Típicamente se usa \(\alpha=0.05\) o \(\alpha=0.01\)

Definición del p-value y errores de interpretación comunes

En un test de hipótesis “de una cola” el p-value se define como la probabilidad de observar un valor del estadístico \(T\) más extremo que el observamos en nuestra muestra, es decir

\[ p = P(T> T_{data} | H_0) \]

Error

El p-value no es es la probabilidad de que \(H_0\) sea cierta dado nuestras observaciones, eso sería:

\[ P(H_0 | T> T_{data}) \]

Otro error común es creer que no ser capaz de rechazar \(H_0\) es lo mismo que aceptar \(H_0\)

Error

No tener suficiente evidencia para rechazar no es lo mismo que aceptar

28.2. El t-test de una muestra#

Sea un conjunto de \(N\) observaciones independientes de una variable aleatoria \(X\). La media muestral de este conjunto \({x_1, x_2, \ldots, x_N}\) es

\[ \bar x = \sum_{i=1}^N x_i \]

El t-test de una muestra busca verificar si \(\bar x\) (media muestral) es significativamente distinta de la media poblacional \(\mu\), en el caso de que no conocemos la varianza poblacional \(\sigma^2\)

Las hipótesis son

  • \(H_0:\) \(\bar x = \mu\)

  • \(H_A:\) \(\bar x \neq \mu\)

(Esto corresponde a un test de dos colas)

Para este test el estadístico de prueba es

\[ t = \frac{\bar x - \mu}{\hat \sigma /\sqrt{N-1}} \]

donde \(\hat \sigma = \sqrt{ \frac{1}{N} \sum_{i=1}^N (x_i - \bar x)^2}\) es la desviación estándar muestral (sesgada)

Asumiendo que \(\bar x\) se distribuye \(\mathcal{N}(\mu, \frac{\sigma^2}{N})\) entonces \(t\) se distribuye t-student con \(N-1\) grados de libertad

Advertencia

Para muestras iid y \(N\) grande el supuesto del t-test se cumple por teorema central del límite. Si \(N\) es pequeño debemos verificar la normalidad de los datos antes de aplicar el t-test

28.3. T-test de una y dos muestras con scipy#

Ejemplo 1: Una investigadora en botánica quiere saber si la áltura promedio de cierta especia de planta es igual a 38 cm (hipótesis nula)

Para esto colecta una muestra aleatoria de 12 plantas y registra su altura:

import numpy as np
import scipy.stats

mu = 38.
alpha = 0.05
data = np.load("data/botany.npy")
data

array([35.56, 35.56, 40.64, 33.02, 30.48, 43.18, 38.1 , 35.56, 38.1 ,
       33.02, 38.1 , 35.56])

Para realizar un t-test de una muestra con scipy utilizamos

result = scipy.stats.ttest_1samp(data, mu, alternative='two-sided')
result

Ttest_1sampResult(statistic=-1.5853482351389023, pvalue=0.1411941997029352)

donde

result.pvalue < alpha

False

No hay suficiente evidencia para rechazar la hipótesis nula

Ejemplo 2: Un médico bioregulador quiere verificar si el gasto energético promedio es menor en personas obesas que en personas no obesas

Para esto evalua una muestra al azar de personas obesas y una muestra al azar de personas delgadas y registra los resultados en la siguiente base de datos:

alpha = 0.05

energy, label = np.load('data/energy.npy').T
sample_control, sample_obese = energy[label==0], energy[label==1]

Para resolver este problema podemos utilizar un t-test de dos muestras. En este test la hipótesis nula es que las medias de ambas muestreas son equivalentes, mientras que la hipótesis alternativa puede ser

  • que las medias muestrales son distintas (dos colas)

  • que la media de la primera muestra es mayor que la de la segunda (una cola)

  • que la media de la primera muestra es menor que la de la segunda (una cola)

Podemos resolver un t-test de dos muestras como el del ejemplo anterior utilizando scipy con

result = scipy.stats.ttest_ind(sample_obese, sample_control, alternative='less')
result

Ttest_indResult(statistic=-3.9455649161549835, pvalue=0.00039949910558502964)

donde

result.pvalue < alpha

True

Rechazamos la hipótesis nula de que los gastos energéticos son iguales

28.4. Test de hipótesis para la regresión lineal#

En un modelo de regresión lineal donde tenemos \(N\) ejemplos

\[ y_i = x_i \theta_1 + \theta_0, ~ i=1, 2, \ldots, N \]

nos interesa probar que la correlación entre \(x\) es \(y\) es significativa. Podemos hacer esto realizando un test sobre el parámetro \(\theta_1\)

Por ejemplo podemos plantear las siguientes hipótesis

  • \(H_0:\) La pendiente es nula \(\theta_1 = 0\) (no hay correlación entre \(x\) e \(y\))

  • \(H_A:\) La pendiente no es nula: \(\theta_1 \neq 0\)

(test de dos colas)

Asumiendo que \(\theta_1\) se distribuye normal con varianza desconocida podemos formular el siguiente estadístico de prueba

\[ t = \frac{(\theta_1-\theta^*) }{\text{SE}_{\theta_1}/\sqrt{N-2}} = \frac{ r\sqrt{N-2}}{\sqrt{1-r^2}}, \]

donde \(r \in [-1, 1]\) es el coeficiente de correlación de Pearson, el cual es comunmente utilizado para medir la fuerza de la correlación

  • si \(r=1\) existe una correlación lineal perfecta

  • si \(r=-1\) existe una anticorrelación lineal perfecta

  • si \(r=0\) no hay correlación lineal entre las variables

Nota

En general un \(r>0.5\) se considera una correlación importante

La última igualdad en la expresión de \(t\) se obtiene reemplazando \(\theta^*=0\) y

\[ \text{SE}_{\theta_1} = \sqrt{ \frac{\frac{1}{N} \sum_i (y_i - \hat y_i)^2}{\text{Var}(x)}}. \]

Nota

Si \(\theta_1\) es normal entonces el estadístico \(t\) tiene distribución t-student con dos grados de libertad (modelo de dos parámetros)

Ejercicio formativo

Sea el dataset de consumo de helados que utilizamos en lecciones anteriores

import pandas as pd
df = pd.read_csv('../linalg/data/helados.csv', header=0, index_col=0)
df.columns = ['consumo', 'ingreso', 'precio', 'temperatura']
display(df.head())
consumo ingreso precio temperatura
1 0.386 78 0.270 41
2 0.374 79 0.282 56
3 0.393 81 0.277 63
4 0.425 80 0.280 68
5 0.406 76 0.272 69

Podemos resolver un problema de regresión lineal univariado con scipy utilizando

scipy.stats.linregress(x, # Variable independiente unidimensional
                       y # Variable dependiente unidimensional
                      )

Esta función retorna una tupla con

  • Valor de la pendiente: \(\theta_1\)

  • Valor de la intercepta: \(\theta_0\)

  • Coeficiente de correlación \(r\)

  • p-value

  • Error estándar del ajuste

Para el ejemplo anterior podemos ajustar regresiones lineales entre consumo y las demás variables:

%matplotlib inline
import matplotlib.pyplot as plt

fig, ax = plt.subplots(1, 3, figsize=(8, 3), tight_layout=True, sharey=True)
ax[0].set_ylabel(df.columns[0]);
for ax_, col in zip(ax, df.columns[1:]):
    res = scipy.stats.linregress(df[col], df["consumo"])
    x_plot = np.linspace(np.amin(df[col]), np. amax(df[col]), num=100)
    ax_.scatter(df[col], df["consumo"], label='datos', s=10)    
    ax_.plot(x_plot, res.slope*x_plot + res.intercept, lw=2, c='r', label='modelo');
    ax_.set_xlabel(col)
    ax_.set_title(f"$r$: {res.rvalue:0.5f}")
ax_.legend();
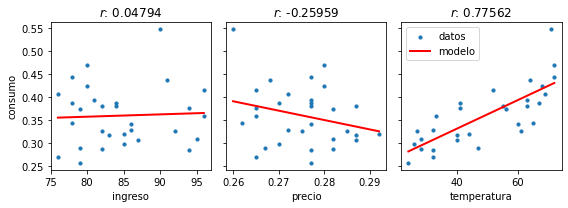
../../_images/fd6bb1786baf4e22a669e14f756277b24b8f1ca3253916eeeb845cadc274f573.png

Es decir que visualmente parece existir

  • una correlación cercana a cero entre consumo e ingreso

  • una correlación negativa moderada entre consumo y precio

  • una correlación positiva alta entre consumo y temperatura

La función linregress implementa el t-test sobre \(\theta_1\) que vimos anteriormente. Usemos estos resultados para verificar si las correlaciones son estadísticamente significativas

alpha = 0.05

for i, col in enumerate(df.columns[1:]):
    res = scipy.stats.linregress(df[col], df["consumo"])
    print(f"{col}: \t Rechazo hipótesis nula: {res.pvalue < alpha}")    

ingreso: 	 Rechazo hipótesis nula: False
precio: 	 Rechazo hipótesis nula: False
temperatura: 	 Rechazo hipótesis nula: True

Como complemento visualizemos

  • las distribuciones bajo la hipótesis nula: linea azul

  • los límites dados por \(\alpha\): linea punteada negra (dos colas)

  • El valor del observado para cada una de las variables: linea roja

fig, ax = plt.subplots(1, 3, figsize=(8, 2), tight_layout=True, sharey=True)
ax[0].set_ylabel(df.columns[0]);

N = df.shape[0]
t = np.linspace(-7, 7, num=1000)
dist = scipy.stats.t(loc=0, scale=1, df=N-2) # dos grados de libertad


for i, col in enumerate(df.columns[1:]):
    res = scipy.stats.linregress(df[col], df["consumo"])
    t_data = res.rvalue*np.sqrt(N-2)/np.sqrt(1.-res.rvalue**2)
    ax[i].plot(t, dist.pdf(t))
    ax[i].plot([dist.ppf(alpha/2)]*2, [0, np.amax(dist.pdf(t))], 'k--')
    ax[i].plot([dist.ppf(1-alpha/2)]*2, [0, np.amax(dist.pdf(t))], 'k--')
    ax[i].plot([t_data]*2, [0, np.amax(dist.pdf(t))], 'r-')
    ax[i].set_xlabel(col)
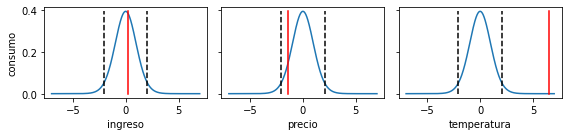
../../_images/3558930c127cdc4af13d875ce1467d6b60f902cd9ad8acf5ce97d80fa355e985.png

Por lo tanto

Rechazamos la hipótesis nula de que no existe correlación entre temperatura y consumo con un 95% de confianza

Para las variables ingreso y precio no existe suficiente evidencia para rechazar la hipótesis nula

28.5. Reflexión final#

En el ejercicio anterior usamos un t-test para una regresión lineal entre dos variables

¿Qué prueba puedo usar si quiero hacer regresión lineal multivariada?

Se puede usar un f-test o ANOVA

¿Qué pasa si…

  • los datos tienen una relación que no es lineal?

  • \(\theta_1\) no es Gaussiano/normal?

  • si el ruido de los datos no es Gaussiano?

En estos casos no se cumplen los supuestos del modelo o del test, por ende el resultado no es confiable

Consejo

Si los supuestos no se cumplen para ninguna prueba parámetrica se puede probar con pruebas no-paramétricas. Las pruebas no parámetricas no presuponen una distribución para los estadísticos de prueba pero suele ser menos poderosas que sus contrapartes paramétricas

28.6. Apéndice: Interpretación probabilística de la regresión lineal#

Sea un problema de regresión lineal donde queremos predecir \(y\) en función de \(x\). Para esto proponemos un modelo de dos parámetros

\[ f_i = \theta_0 + \theta_1 x_i \]

Y asumimos que las observaciones son una combinación aditiva del modelo y ruido

\[ y_i = f_i + \epsilon_i \]

donde \(\epsilon_i \sim \mathcal{N}(0, \sigma^2)\), es decir que el ruido es independiente, normal y con media cero. Por lo tanto

\[ y_i \sim \mathcal{N}(f_i, \sigma^2) \]

y en consecuencia el estimador de máxima verosimilitud para \(\theta\) es

\[\begin{split} \begin{split} \hat \theta &= \text{arg}\max_\theta \log \mathcal{L}(\theta) \\ &=\text{arg}\max_\theta \sum_{i=1}^N -\frac{(y_i - f_i)^2}{2\sigma^2} \\ &=\text{arg}\max_\theta - \frac{1}{2\sigma^2} \sum_{i=1}^N (y_i - \theta_0 - \theta_1 x_i)^2 \\ &=\text{arg}\min_\theta \sum_{i=1}^N (y_i - \theta_0 - \theta_1 x_i)^2 \end{split} \end{split}\]

Es decir que el estimador de máxima verosimilitud es equivalente a la solución de mínimos cuadrados ordinarios que vimos anteriormente

Importante

Cuando utilizamos la solución de mínimos cuadrados estamos asumiendo implicitamente que las observaciones son iid y que la verosimilitud es Gaussiana

Derivando con respecto a los parámetros e igualado a cero tenemos que

\[\begin{split} \begin{split} \sum_i y_i - N\theta_0 - \theta_1 \sum_i x_i &= 0 \\ \sum_i y_i x_i - \theta_0 \sum_i x_i - \theta_1 \sum_i x_i^2 &= 0 \end{split} \end{split}\]

y despejando lo anterior

\[\begin{split} \begin{split} \theta_0 &= \bar y - \theta_1 \bar x \\ \theta_1 &= \frac{\sum_i x_i y_i - N \bar x \bar y}{\sum_i x_i^2 - M \bar x^2} \\ &= \frac{ \sum_i (y_i - \bar y)(x_i - \bar x)}{\sum_i (x_i - \bar x)^2} = \frac{\text{COV}(x, y)}{\text{Var}(x)} \end{split} \end{split}\]

de donde reconocemos las expresiones para la covarianza entre \(x\) e \(y\) y la varianza de \(x\)

Estas son las soluciones que implementa scipy.stats.linregress