33. Clasificador Bayesiano “Ingenuo”

33.1. Formalismo matemático

El clasificador bayesiano busca la probabilidad de la etiqueta \(y\) dado el ejemplo \(x\), es decir \(P(y|x)\). Usando el teorema de Bayes podemos escribir esto como

\[ p(y | x) = \frac{p(x|y) p(y)}{p(x)} = \frac{p(x|y) p(y)}{\sum_{y\in\mathcal{Y}} p(x|y) p(y)} \]

donde

• \(p(y)\) es la probabilidad a priori, corresponde a lo que sabemos antes de observar el ejemplo

• \(p(y|x)\) es la probabilidad a posteriori, corresponde a lo que sabemos luego de observar el ejemplo \(x\)

• \(p(x|y)\) es la verosimilitud de observar un ejemplo con atributos \(x\) suponiendo que la etiqueta es \(y\)

Si tenemos un problema de clasificación binario, es decir con dos etiquetas, podemos escribir

\[ \frac{p(y=1|x)}{p(y=0|x)} = \frac{p(x|y=1) p(y=1)}{p(x|y=0) p(y=0)} \]

Si el cociente anterior es mayor que \(1\) entonces la clase de \(x\) es \(1\), de lo contrario es \(0\). Si tenemos un problema de clasificación con \(C\) clases entonces decidimos la clase con

\[ \hat y = \text{arg}\max_{k=1,\ldots,C} p(x|y=k) p(y=k) \]

En ambos casos el denominador del teorema de Bayes no se ocupa, pues es idéntico para todo \(y\). Por otro lado el prior suele estimarse empíricamente a partir de la base de datos de entrenamiento como

\[ p(y=k) = \frac{\text{Cantidad de ejemplos con etiqueta k}}{\text{Cantidad de ejemplos}} \]

En términos prácticos la principal ventaja de este clasificador es que es simple, fácil de entrenar y muy difícil de sobreajustar. Su mayor desventaja es que hace supuestos muy fuertes sobre los datos. Si no se cumplen el desempeño no será bueno.

33.2. Supuestos “ingenuos”

Sea \(x\) un vector que representa \(D\) atributos. El primer supuesto del clasificador bayesiano ingenuo es que los atributos son independientes. Por lo tanto la verosimilitud se puede escribir como

\[ p(x|y) = \prod_{d=1}^D p(x_d|y) \]

En segundo lugar se debe suponer una distribución para los atributos. Por ejemplo si asumimos una distribución Gaussiana

\[ p(x_d|y) = \mathcal{N}(\mu_d, \sigma_d^2) \]

se tiene un clasificador bayesiano ingenuo con verosimilitud Gaussiana. Se pueden suponer otras distribuciones dependiendo de los datos

• La distribución Gaussiana es típicamente usada para atributos continuos

• Para atributos discretos se puede usar la distribución multinomial

33.3. Ejemplo: Clasificación de biopsias

En este ejemplo implementaremos un clasificador bayesiano ingenuo con verosimilitud gaussiana y lo entrenaremos usando el dataset de cancer de mama de la Universidad de Wisconsin. Para simplificar utilizaremos sólo dos atributos por paciente:

• x: radio de la muestra (valor continuo)

• z: textura de la muestra (valor continuo)

Adicionalmente la variable \(y\) se refiere a la etiqueta de la muestra que puede ser benigno o maligno.

Importemos los datos y analicemos un gráfico de dispersión de los atributos. Reflexione ¿Son los datos separables?

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from functools import partial
import pandas as pd

df = pd.read_csv('data/cancer.csv', index_col=0)
X, y = df.drop(columns="diagnosis").values, df["diagnosis"].replace({'M':1, 'B':0}). values

fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)
for k, (label, marker) in enumerate(zip(['Benigno', 'Maligno'], ['o', 'x'])):
    ax.scatter(X[y==k, 0], X[y==k, 1], s=20, marker=marker, label=label, alpha=0.5)
ax.set_xlabel('Radio de la muestra')
ax.set_ylabel('Textura de la muestra')
plt.legend();

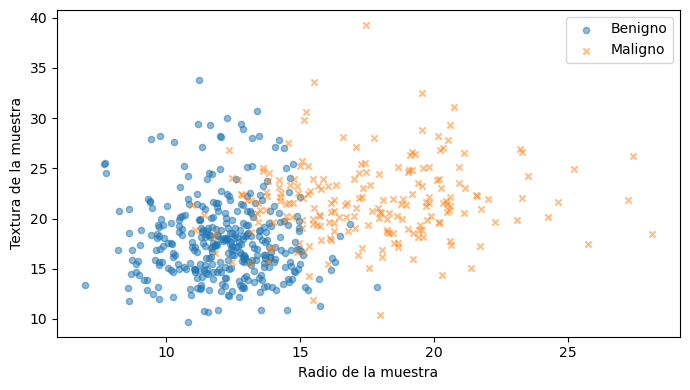
Al ser un problema de clasificación binaria podemos escribir

\[ \frac{p(y=1|x, z)}{p(y=0|x, z)} = \frac{p(x|y=1) p(z|y=1) p(y=1)}{p(x|y=0) p(z|y=0) p(y=0)} \]

from collections import Counter

print(Counter(y))
py = [Counter(y)[i]/len(y) for i in range(2)]

Counter({0: 357, 1: 212})

El dataset tiene 569 pacientes, 212 con tumores malignos (1) y 357 tumores benignos (0).Con esta información estimamos los priors, es decir:

\[ p(y=1) = \frac{212}{569} \approx 0.41 \]

y

\[ p(y=0) = \frac{357}{569} \approx 0.59 \]

Ahora sólo falta encontrar los parámetros \(\mu_x, \sigma_x, \mu_z, \sigma_z\). Los podemos encontrar aplicando el criterio de máxima verosimilitud sobre una distribución normal univariada mediante scipy.stats.norm.fit

import scipy.stats

dists = {}
for y_ in [0, 1]: # Para cada clase
    for d in [0, 1]: # para cada característica
        params = scipy.stats.norm.fit(X[y==y_, d])
        dists[(y_, d)] = scipy.stats.norm(loc=params[-2], scale=params[-1])

El siguiente gráfico de contornos muestra el resultado del ajuste para las distribuciones de los pacientes sanos y con cancer

def verosimilitud_y_cociente(x, z):
    pxzy0 = dists[(0, 0)].pdf(x)*dists[(0, 1)].pdf(z)
    pxzy1 = dists[(1, 0)].pdf(x)*dists[(1, 1)].pdf(z)
    return pxzy0, pxzy1, (pxzy1*py[1])/(pxzy0*py[0] + 1e-8)

fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)
for k, (label, marker) in enumerate(zip(['Benigno', 'Maligno'], ['o', 'x'])):
    ax.scatter(X[y==k, 0], X[y==k, 1], c='k', s=20, 
               marker=marker, label=label, alpha=0.4)

x_plot = np.linspace(np.amin(X[:, 0]), np.amax(X[:, 0]), num=500)
z_plot = np.linspace(np.amin(X[:, 1]), np.amax(X[:, 1]), num=500)

X_2d, Z_2d = np.meshgrid(x_plot, z_plot)
Y_2d = verosimilitud_y_cociente(X_2d, Z_2d)
ax.contour(X_2d, Z_2d, Y_2d[0], zorder=-1, cmap=plt.cm.Reds, levels=20)
ax.contour(X_2d, Z_2d, Y_2d[1], zorder=-1, cmap=plt.cm.Blues, levels=20)
ax.set_xlim([np.amin(x_plot), np.amax(x_plot)])
ax.set_ylim([np.amin(z_plot), np.amax(z_plot)])
ax.set_xlabel('Radio de la muestra (x)')
ax.set_ylabel('Textura de la muestra (z)')
plt.legend();

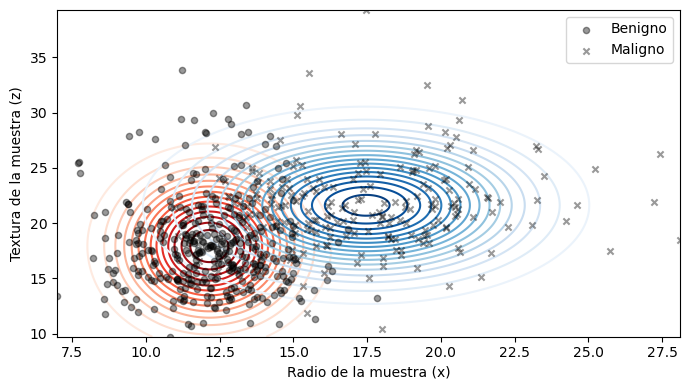
El último paso consiste en decidir entre benigno y maligno usando el cociente entre los posterior

En el caso binario es típico usar una regla como la siguiente

\[ \frac{p(y=1|x, z)}{p(y=0|x, z)} > R \]

donde \(R\) es un “umbral de clasificación”. El siguiente gráfico muestra las fronteras de decisión usando cuatro umbrales distintos

fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)
for k, (label, marker) in enumerate(zip(['Benigno', 'Maligno'], ['o', 'x'])):
    ax.scatter(X[y==k, 0], X[y==k, 1], c='k', s=20, 
               marker=marker, label=label, alpha=0.5)

cp = ax.contour(X_2d, Z_2d, Y_2d[2] , levels=[0.1, 0.5, 1., 1.5], cmap=plt.cm.tab10);
ax.clabel(cp, fontsize=15, fmt='%0.1f', manual=[(9.0, 35), (9.0, 30), (9.0, 22), (12.5, 35)]);

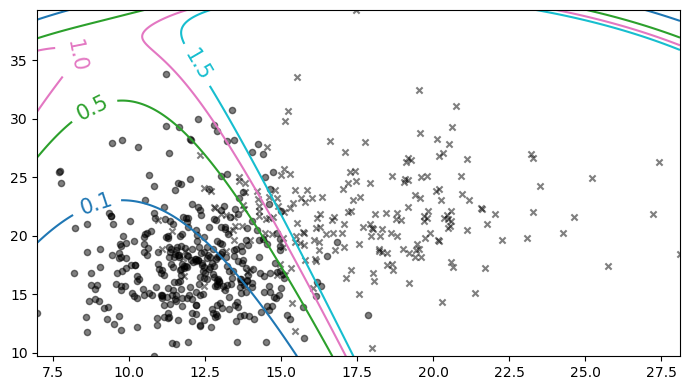
Podemos “ajustar” el riesgo \(R\) para controlar el compromiso (trade-off) entre los siguientes tipos de errores

1. Falso positivo: Predecir que el paciente está enfermo \(\hat y=1\) cuando en realidad estaba sano \(y=0\)

2. Falso negativo: Predecir que el paciente está sano \(\hat y=0\) cuando en realidad estaba enfermo \(y=1\)

Reflexione: En un problema de índole médico como el que acabamos de revisar ¿Cuáles son las repercusiones de cada uno de estos errores? ¿Cuál es más grave?

33.4. Clasificador bayesiano con scikit-learn

A continuación se utiliza el módulo sklearn.naive_bayes que implementa distintos clasificadores bayesianos ingenuos, entre ellos

• Clasificador con verosimilitud Gaussiana: GaussianNB

• Clasificador con verosimilitud Multinomial: MultinomialNB

Por ejemplo el constructor de GaussianNB es

sklearn.naive_bayes.GaussianNB(priors=None, # Un ndarray con las probabilidades a priori
                               ...
                              )

Nota

Si los priors no se especifican se estiman desde la etiqueta al momento de llamar el método fit

cuyos métodos más importantes son

• fit(X, y): Ajusta el modelo a un conjunto de datos X con etiqueta y

• predict_proba(X): Retorna la probabilidad de cada clase

• predict(X): Retorna la clase de máxima probabilidad

• score(X, y): Retorna la exactitud (accuracy) promedio del modelo

Usemos lo aprendido para entrenar el clasificador bayesiano en los datos del ejemplo anterior

from sklearn.naive_bayes import GaussianNB

clf = GaussianNB(priors=py) #Usamos los priors calculados antes
clf.fit(X[:, :2], y) # Entrenamos

GaussianNB(priors=[0.6274165202108963, 0.37258347978910367])

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Podemos uar el método predict_proba para visualizar la frontera de decisión

fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)
for k, (label, marker) in enumerate(zip(['Sanos', 'Cancer'], ['o', 'x'])):
    ax.scatter(X[y==k, 0], X[y==k, 1], c='k', s=20, 
               marker=marker, label=label, alpha=0.5)

Y_2d = clf.predict_proba(np.stack((X_2d.ravel(), Z_2d.ravel())).T)[:, 1]
#Y = clf.predict(np.stack((X.ravel(), Z.ravel())).T)

cf = ax.contourf(X_2d, Z_2d, np.reshape(Y_2d, X_2d.shape), 
                 zorder=-1, cmap=plt.cm.RdBu, vmin=0, vmax=1, levels=20, alpha=0.75)
ax.set_xlim([np.amin(x_plot), np.amax(x_plot)])
ax.set_ylim([np.amin(z_plot), np.amax(z_plot)])
ax.set_xlabel('Radio de la muestra (x)')
ax.set_ylabel('Textura de la muestra (z)')
plt.colorbar(cf)
plt.legend();

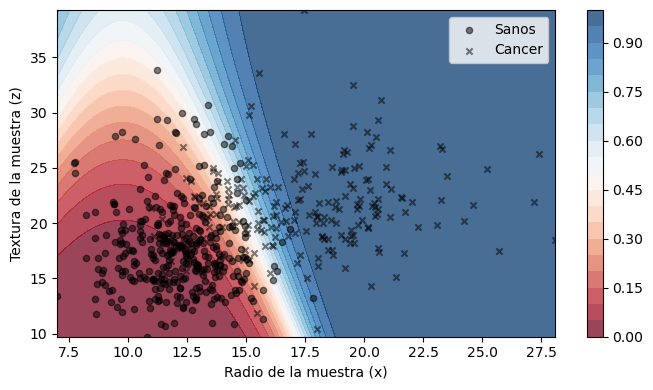
En la próxima lección veremos como evaluar el desempeño de nuestro clasificador entrenado