23. Ecuaciones Diferenciales Ordinarias

Una ecuación diferencial es una ecuación que relaciona una función con sus derivadas. Un caso particular de ecuación diferencial son los sistemas de ecuaciones diferenciales ordinario (EDO)

Para \(y = f(t)\) una EDO tiene la siguiente forma general

\[ \frac{\partial^n y}{\partial t^n} = F \left( t, y, \frac{\partial y}{\partial t}, \frac{\partial^2 y}{\partial t^2}, \ldots, \frac{\partial^{n-1} y}{\partial t^{n-1}} \right) \]

Es decir donde la n-esima derivada de \(f(t)\) puede escribirse como una función de \(t\) y sus derivadas de orden menor. A continuación veremos un ejemplo de sistema EDO y como resolverlo utilizando scipy

El atractor de Lorenz es un sistema EDO de primer orden que fue diseñado para describir como el aire se mueve por la atmósfera (convexión). El sistema tiene tres ecuaciones

\[\begin{split} \begin{split} \frac{du}{dt} &= \sigma(v-u) \\ \frac{dv}{dt} &= \rho u -v - uw \\ \frac{dw}{dt} &= uv - \beta w \end{split} \end{split}\]

donde \(\sigma\), \(\beta\) y \(\rho\) son los parámetros del sistema y \(u(0)\), \(v(0)\) y \(w(0)\) suscondiciones iniciales

Nota

El sistema de Lorenz es un ejemplo de sistema caótico: Pequeños cambios en las condiciones iniciales y en los parámetros generan grandes cambios en el resultado

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import scipy.integrate

23.1. Resolviendo ODEs de primer orden con Scipy

Utilizaremos el submódulo scipy.integrate para resolver el sistema. En particular usaremos la función solve_ivp

En primer lugar debemos escribir el sistema de ecuaciones como una función de Python con la forma

def fun(t, y, *args):
    ...
    return dy

donde t es la variable independiente, y son las variables del sistema y dy son sus derivadas

sigma, beta, rho = 8., 1.6, 28

def lorenz_system(t, y, *args):
    sigma, beta, rho = args
    u, v, w = y
    du = sigma*(v - u)
    dv = rho*u - v - u*w
    dw = u*v -beta*w
    return du, dv, dw

Luego debemos definir las condiciones iniciales, por ejemplo

u0, v0, w0 = 0, 1, 1.05

También debemos entregar un intervalo para la variable independiente

Por ejemplo si queremos que el sistema parta en \(t=0\) (condición inicial) y se resuelva hasta \(t=100\)

span = (0, 100)

Lo último que debemos facilitar es un arreglo que represente los valores de la variable independiente \(t\) donde queremos evaluar \(y\)

Esto debe ser un arreglo contenido dentro de span, por ejemplo

t = np.linspace(0, 100, num=10000)

Finalmente resolvemos la EDO con

result = scipy.integrate.solve_ivp(fun=lorenz_system, 
                                   y0=(u0, v0, w0), 
                                   t_span=span, 
                                   t_eval=t,
                                   args=(sigma, beta, rho))

El objeto result tiene entre sus atributos principales:

• t: Un vector con los instantes de tiempo

• y: Una matriz con los valores de y evaluado en cada uno de los instantes de tiempo

• message: Un mensaje que indica si la razón de término del algoritmo

En este caso:

t = result.t
u, v, w = result.y

result.message

'The solver successfully reached the end of the integration interval.'

23.2. Visualización del atractor de Lorenz

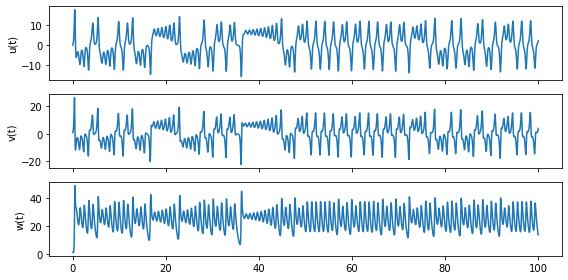
A continuación se visualiza la evolución en el tiempo de las variables del sistema

fig, ax = plt.subplots(3, figsize=(8, 4), 
                       tight_layout=True, sharex=True)
ax[0].plot(t, u); ax[0].set_ylabel('u(t)')
ax[1].plot(t, v); ax[1].set_ylabel('v(t)')
ax[2].plot(t, w); ax[2].set_ylabel('w(t)');

También podemos visualizar en tres dimensiones como se muestra a continuación

from mpl_toolkits.mplot3d import Axes3D

fig, ax = plt.subplots(figsize=(6, 6), subplot_kw={'projection':'3d'})
ax.plot(u, v, w, alpha=0.75)
ax.scatter(u0, v0, w0, s=50)
ax.set_xlabel('u(t)')
ax.set_ylabel('v(t)')
ax.set_zlabel('w(t)');

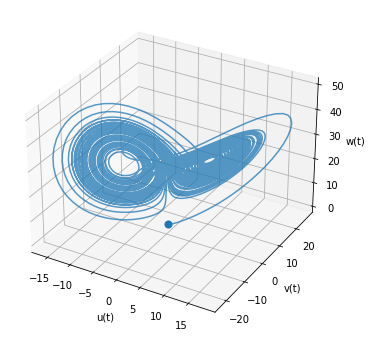
donde el punto marca la condición inicial del sistema

Nota

La solución tiene dos focos de atracción los cuales recorre con distintas orbitas

No es un sistema periódico pues siempre hace orbitas distintas. Tampoco es un sistema estocástico, pues su movimiento sigue un patrón determinista. Eso es la característica del caos

When the present determines the future, but the approximate present does not approximately determine the future

—Edward Lorenz

Ejercicio propuesto: El sistema de Lorenz cambia de comportamiento drasticamente con sus condiciones iniciales y sus parámetros. Implemente un dashboard con sliders para \(u(0)\), \(v(0)\), \(w(0)\), \(\sigma\), \(\beta\) y \(\rho\) que actualicen el gráfico 3d anterior

Ver también

Otro sistema caótico emblemático: https://geoffboeing.com/2015/03/chaos-theory-logistic-map/