6. Máquinas de soporte vectorial

Una máquina de soporte vectorial (support vector machine, SVM) es un modelo de aprendizaje supervisado que busca que un hiperplano óptimo

\[ h(x) = \langle w, x \rangle + b \]

para separar un conjunto de datos

\[ D = \{(x_1, y_1), (x_2, y_2), \ldots (x_N, y_N)\} \]

donde \(x_i \in \mathbb{R}^M\) con etiquetas \(y_i \in \{-1, +1\}\).

Considere los siguientes hiperplanos separadores:

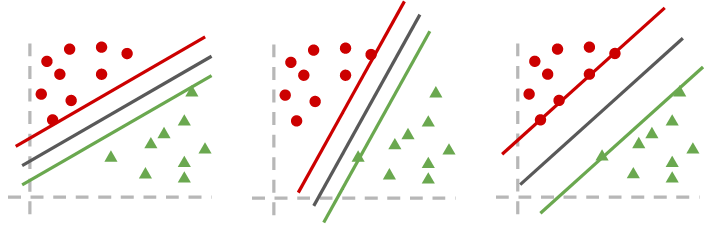
Para la SVM el hiperplano óptimo es el de más a la derecha: aquel que tiene máximo margen.

Margen (\(\tau\))

Distancia del hiperplano a la muestra más cercana

A continuación veremos el problema de optimización planteado por la SVM para obtener el hiperplano óptimo.

6.1. Formulación primal de la SVM

La formulación primal se obtiene definiendo las siguientes condiciones

• Para \(y_i = +1\) se tiene \(\langle w, x_i \rangle + b \geq 1\)

• Para \(y_i = -1\) se tiene \(\langle w, x_i \rangle + b \leq 1\)

que pueden escribirse como de forma resumida como

\[ y_i \left(\langle w, x_i \rangle + b\right) \geq 1 \]

donde llamamos vectores de soporte a los ejemplos \((x_i, y_i)\) que cumplen con

\[ y_i \left(\langle w, x_i \rangle + b\right) = 1 \]

Importante

Los vectores de soporte definen el hiperplano separador.

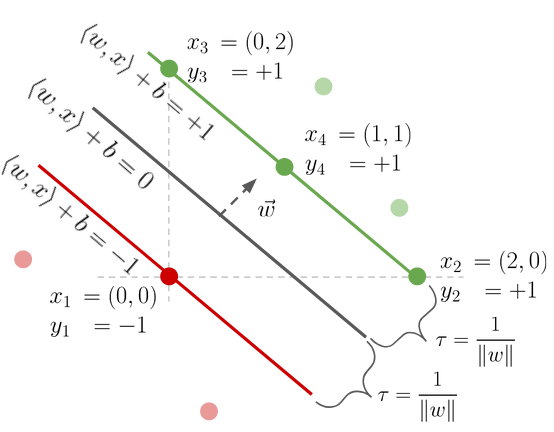
La figura muestra un hiperplano (linea negra) que separa datos de dos clases representados por puntos verdes y rojos, respectivamente.

• El ejemplo \(x_1\) es un vector de soporte asociado a la clase \(-1\)

• Los ejemplos \(x_2\), \(x_3\) y \(x_4\) son vectores de soporte de la clase \(+1\)

• El margen entre el hiperplano y los vectores de soporte es \(\tau = \frac{1}{\|w\|}\)

Considerando las ecuaciones anteriores como restricciones y planteando el objetivo de maximizar el margen se tiene la formulación primal de la SVM:

\[\begin{split} \begin{split} \min_{w,b} &\frac{1}{2}\|w\|^2 \\ \text{sujeto a: }& y_i \left(\langle w, x_i \rangle + b\right) \geq 1, \forall i \end{split} \end{split}\]

Este problema se resuelve utilizando multiplicadores de Lagrange.

Ejercicio propuesto: Plantee las restricciones de la formulación primal para los datos de la figura anterior y despeje el valor de \(w\) y \(b\). Solución: \(w= (1,1)\) y \(b=-1\).

6.2. Formulación dual de la SVM

A partir de la formulación primal podemos definir el lagrangiano como

\[ L(w, b, \alpha) = \frac{1}{2}\|w\|^2 - \sum_{i=1}^N \alpha_i \left [ y_i \left(\langle w, x_i \rangle + b\right) - 1 \right] \]

donde \(\alpha_i\) son los multiplicadores de Lagrange.

Derivando en función de \(w\) y \(b\) e igualando a cero tenemos

\[ \sum_{i=1}^N \alpha_i y_i = 0 \]

y

\[ w = \sum_{i=1}^N \alpha_i y_i x_i \]

Reemplazando esta definición de \(w\) en el lagrangiano se obtiene la formulación dual de la SVM:

\[\begin{split} \begin{split} \max_\alpha \sum_{i=1}^N \alpha_i - &\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\langle x_i, x_j \rangle \\ \text{sujeto a:} &\sum_{i=1}^N \alpha_i y_i = 0 \\ &\alpha_i \geq 0, \forall i \end{split} \end{split}\]

Por otra parte el hiperplano dual es

\[ h(x) = \sum_{i=1}^N \alpha_i y_i \langle x, x_i \rangle + b \]

donde

\[ b = y_k - \langle w, x_k \rangle \]

para algún \(k\) tal que \(\alpha_k > 0\).

Nota

Los vectores de soporte son los ejemplos donde \(\alpha_i > 0\). En cambio para los ejemplos que no son vectores de soporte se tiene \(\alpha_i=0\)

Ejercicio: Considere el dataset que se muestra en la siguiente figura:

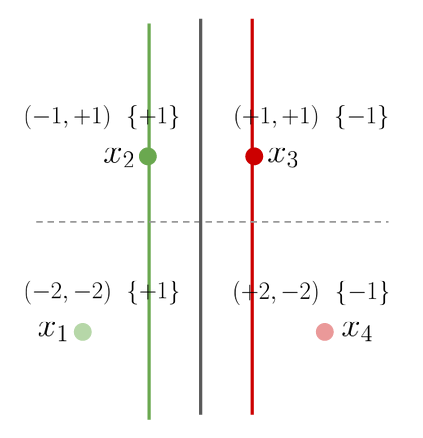
donde se han demarcado los vectores de soporte y el hiperplano de máxima separación. Obtenga los parámetros del hiperplano separador utilizando la formulación primal y luego la dual.

6.3. Margen relajado de la SVM

Las formulaciones anteriores no consideran el caso en que existan errores, es decir ejemplos que quedan del lado contrario de la frontera de decisión.

Llamamos a estos ejemplos no separables y les asignamos una variable de compensación \(\xi\) como muestra la siguiente figura:

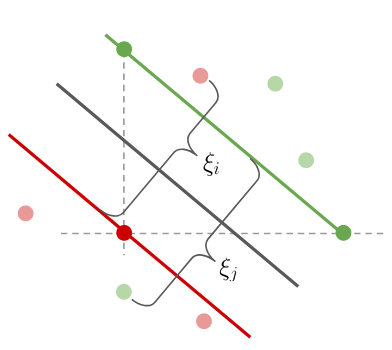
Con las variables de compensación, la formulación primal de la SVM cambia a:

\[\begin{split} \begin{split} \min_{w,b} &\frac{1}{2}\|w\|^2 + C \sum_{i=1}^N \xi_i \\ \text{sujeto a: }& y_i \left(\langle w, x_i \rangle + b\right) \geq 1 - \xi_i, \forall i \\ &\xi_i \geq 0, \forall i \end{split} \end{split}\]

donde se ha agregado \(C>0\) que pondera la regularización de la función de costo.

Nota

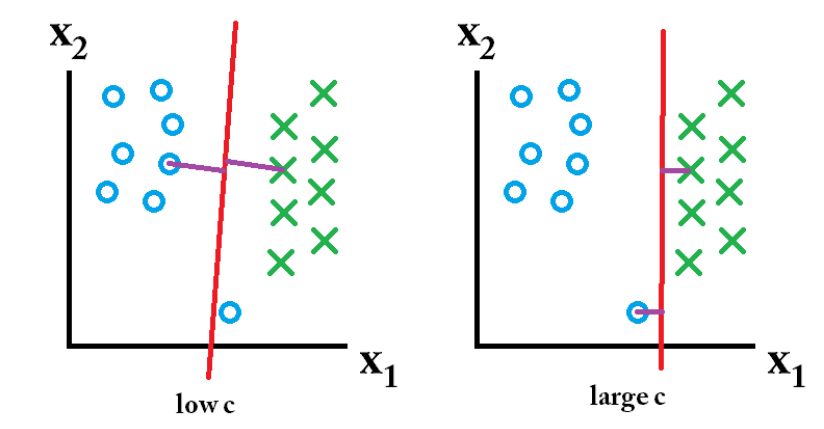
El hiperparámetro \(C\) controla el trade-off entre la minimización del margen y la cantidad de ejemplos mal clasificados

• Un valor grande de \(C\) privilegia un hiperplano de margen pequeño con pocos errores

• Un valor pequeño de \(C\) privilegia un hiperplano de gran margen con muchos errores

Si consideramos \(C\) la formulación dual cambia a:

\[\begin{split} \begin{split} \max_\alpha \sum_{i=1}^N \alpha_i - &\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\langle x_i, x_j \rangle \\ \text{sujeto a:} &\sum_{i=1}^N \alpha_i y_i = 0 \\ &C > \alpha_i \geq 0, \forall i \end{split} \end{split}\]

6.4. Transformación no lineal de los datos

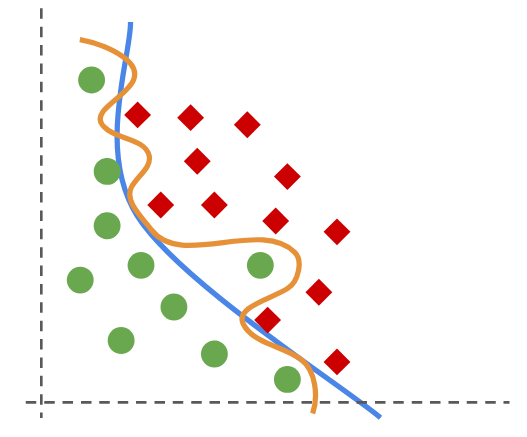
La SVM es capaz de encontrar fronteras lineales (hiperplanos) para separar los datos de entrenamiento, pero

¿Qué ocurre si en primer lugar nuestros datos no son linealmente separables?

Considere el siguiente ejemplo donde las clases se agrupan como dos circulos concéntricos:

import numpy as np
from sklearn.datasets import make_circles

np.random.seed(12345)
X, y = make_circles(noise=0.1, factor=0.1)

non_linear_transform = lambda x : np.stack((x[:, 0], x[:, 1], x[:, 0]**2 + x[:, 1]**2)).T

PhiX = non_linear_transform(X)

%matplotlib inline
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(8, 4), tight_layout=True)
ax = fig.add_subplot(1, 2, 1)
for y_ in np.unique(y):
    ax.scatter(X[y==y_, 0], X[y==y_, 1], label=f'clase {y_}', 
               c=y[y==y_], cmap=plt.cm.RdBu_r, vmin=0, vmax=1)
ax.set_title('Espacio original')
ax.legend()
ax = fig.add_subplot(1, 2, 2, projection='3d')    
for y_ in np.unique(y):
    ax.scatter(PhiX[y==y_, 0], PhiX[y==y_, 1], PhiX[y==y_, 2],
               c=y[y==y_], cmap=plt.cm.RdBu_r, vmin=0, vmax=1)
ax.view_init(elev=15., azim=45)
ax.set_title('Espacio transformado');

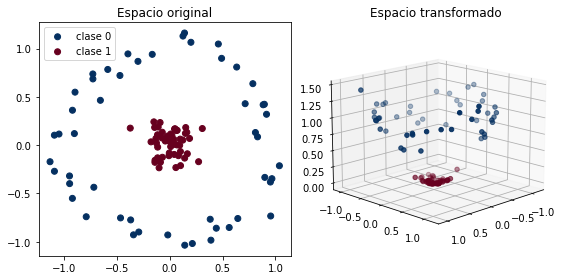
La subfigura izquierda muestra los datos en su espacio original (dos dimensiones). Claramente no es posible separarlos con un hiperplano.

Considere ahora la siguiente transformación no lineal \(\phi: \mathbb{R}^2 \to \mathbb{R}^3\) definida como

\[ \phi(x) = (x_1, x_2, x_1^2 + x_2^2) \]

La subfigura derecha muestra los datos en el espacio transformado (tres dimensiones). En este espacio si se pueden separar por un hiperplano.

Nota

Generalmente es más fácil encontrar hiperplanos separadores (lineales) en espacios aumentados. El hiperplano en el espacio aumentado corresponde a una frontera no lineal en el espacio de entrada.

6.5. Kernels y SVM

Un kernel (definido positivo) es un producto interno en un espacio de features implícito y generalmente de alta dimensionalidad.

Un kernel \(\kappa: \mathcal{X} \times \mathcal{X} \to \mathbb{R}\) cumple lo siguiente

\[ \kappa(x_i, x_j) = \langle \phi(x_i), \phi(x_j) \rangle \]

donde \(\phi\) es una transformación no lineal que es inducida por el kernel

Nota

La ecuación anterior se conoce como el truco del kernel

Veamos dos kernels ampliamente utilizados. El primero es el kernel polinomial con hiperparámetros \(c_0\), \(d\) y \(\gamma>0\)

\[ \kappa(x_i, x_j) = (c_0 + \gamma \langle x_i, x_j \rangle)^d \]

Por ejemplo para \(d=2\), \(c_0=1\), \(\gamma=1\) y \(x_i \in \mathbb{R}\) este kernel induce una transformación no lineal

\[\begin{split} \begin{split} \kappa(x_i, x_j) &= (1 + x_i x_j)^2 = 1 + 2 x_i x_j + x_i^2 x_j^2 \\&= \left\langle \begin{pmatrix} 1\\ \sqrt{2} x_i \\ x_i^2 \end{pmatrix}, \begin{pmatrix} 1\\ \sqrt{2} x_j \\ x_j^2 \end{pmatrix} \right\rangle \end{split} \end{split}\]

El segundo es el kernel gaussiano o RBF (radial basis function) con hiperparámetro \(\gamma>0\)

\[ \kappa(x_i, x_j) = \exp \left(-\gamma \| x_i - x_j \|^2 \right), \]

cuyo transformación no lineal inducida es

\[\begin{split} \begin{split} \kappa(x_i, x_j) &= \exp \left(-\gamma \| x_i\|^2 \right) \exp \left(-\gamma \| x_j\|^2 \right) \exp \left(\gamma \langle x_i, x_j \rangle \right) \\ &= \exp \left(-\gamma \| x_i\|^2 \right) \exp \left(-\gamma \| x_j\|^2 \right) \sum_{k=1}^\infty \frac{\left(\gamma \langle x_i, x_j \rangle \right)^k}{k!} \end{split} \end{split}\]

Nota

El espacio inducido por el kernel RBF es de dimensionalidad infinita

Advertencia

Controlando \(\gamma\) es muy fácil obtener un espacio donde los datos sean linealmente separables, sin embargo esto puede inducir a sobreajuste, como muestra la siguiente figura

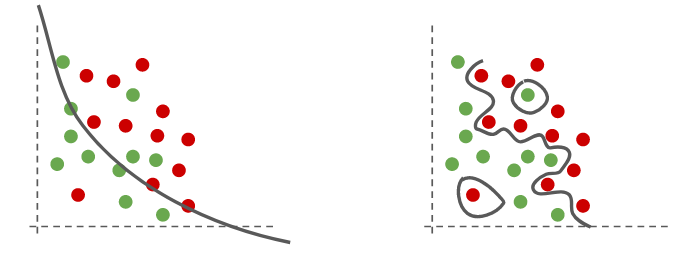
• En la subfigura izquierda se ha utilizado un valor de \(\gamma\) pequeño (hiperplano poco flexible)

• En la subfigura derecha se ha utilizado un valor de \(\gamma\) grande (hiperplano muy flexible)

Consejo

Cuando utilizamos kernels, el hiperparámetro \(C\) cobra mayor relevancia. Utilizando un valor de \(C\) pequeño privilegiamos un hiperplano más suave (menos complejo) con margen ancho (regularización).

Advertencia

Los hiperparámetros de la SVM, como \(\gamma\) y \(C\), son sensibles. Debemos calibrarlos utilizando técnicas de validación.

Utilizando el truco del kernel no es necesario conocer la transformación no lineal \(\phi\). Basta reemplazar \(\langle \phi(x_i), \phi(x_j) \rangle\) por \(\kappa(x_i, x_j)\) en la formulación dual de la SVM como se muestra a continuación:

\[\begin{split} \begin{split} \max_\alpha \sum_{i=1}^N \alpha_i - &\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j \kappa(x_i, x_j)\\ \text{sujeto a:} &\sum_{i=1}^N \alpha_i y_i = 0 \\ &C > \alpha_i \geq 0, \forall i \end{split} \end{split}\]

y el hiperplano utilizando kernels es:

\[ h(x) = \sum_{i=1}^N \alpha_i y_i \kappa(x, x_i) + b \]

6.6. SVM para clasificación con scikit-learn

La librería scikit-learn tiene implementaciónes de la SVM para clasificación y para regresión. La clase de SVM para clasificación es sklearn.svm.SVC.

Sus argumentos principales son

• C: El hiperparámetro de regularización

• kernel: Las opciones son

  • linear: Sin kernel

  • poly: Kernel polinomial (se debe especificar degree y coef0)

  • rbf: Kernel Gaussiano (se debe especificar gamma

  • Una función de Python que corresponda a un kernel matemáticamente válido

• gamma, degree, coef0: Los hiperparámetros de los kernels

• tol: Tolerancia para el criterio de detención del algoritmo

• probability: Booleano que especifica si se deben calcular probabilidades (aumenta el costo computacional)

Sus métodos principales son

• fit(X,y): Entrena la SVM

• predict(X): Retorna predicción dura de X

• predict_proba(X): Retorna la predicción probabilística de X (sólo si probability=True)

• get_params(): Retorna un diccionario con los nombres y valores de los parámetros de la SVM y del kernel

• score(X, y): Retorna el accuraccy promedio del modelo

• decision_function(X): Retorna la frontera de decisión evaluada en X

El resultado para el ejemplo anterior utilizando un kernel lineal es:

from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline

model = make_pipeline(StandardScaler(), 
                      SVC(kernel='linear'))

model.fit(X, y);

Consejo

Se recomienda estandarizar los datos antes de entrenar la SVM para facilitar la optimización numérica.

Con decision_function podemos visualizar la frontera de decisión el espacio original. En este caso un kernel lineal es claramente inapropiado para el problema.

def plot_decision_boundary(model, ax, xmin=-1.5, xmax=1.5, title=None):
    x = np.linspace(xmin, xmax, num=100)
    xx, yy = np.meshgrid(x, x)
    hiperplane = model.decision_function(np.stack((xx.ravel(), yy.ravel())).T).reshape(xx.shape)
    
    ax.pcolormesh(xx, yy, hiperplane, cmap=plt.cm.RdBu_r)
    ax.scatter(X[:, 0], X[:,1], c='k', alpha=0.5, s=20)
    if title is not None:
        ax.set_title(title)
    
fig, ax = plt.subplots(figsize=(4, 4), tight_layout=True)
plot_decision_boundary(model, ax)

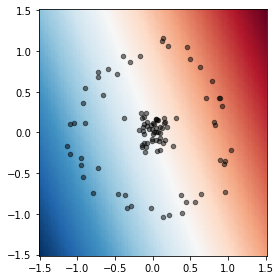
Intentemos ahora con un kernel Gaussiano y veamos la influencia de gamma en el hiperplano separador:

from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline

fig, ax = plt.subplots(2, 3, figsize=(8, 6), tight_layout=True)

for ax_, gamma_ in zip(ax.ravel(), [0.001, 0.01, 0.1, 1.0, 10., 100.]):
    model = make_pipeline(StandardScaler(), 
                          SVC(C=1, kernel='rbf', gamma=gamma_))

    model.fit(X, y)
    plot_decision_boundary(model, ax_, title=f'gamma: {gamma_}')

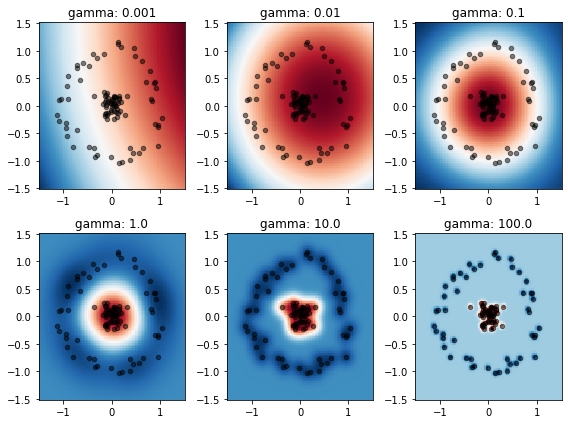
Nota

Un valor pequeño de \(\gamma\) produce un hiperplano demasiado suave. Mientras que un valor demasiado grande produce un hiperplano muy flexible que se sobreajusta facilmente a los datos

Podemos realizar validación cruzada de los parámetros más relevantes utilizando las herramientas de Scikit-learn:

model = make_pipeline(StandardScaler(), SVC())
model.get_params()

{'memory': None,
 'steps': [('standardscaler', StandardScaler()), ('svc', SVC())],
 'verbose': False,
 'standardscaler': StandardScaler(),
 'svc': SVC(),
 'standardscaler__copy': True,
 'standardscaler__with_mean': True,
 'standardscaler__with_std': True,
 'svc__C': 1.0,
 'svc__break_ties': False,
 'svc__cache_size': 200,
 'svc__class_weight': None,
 'svc__coef0': 0.0,
 'svc__decision_function_shape': 'ovr',
 'svc__degree': 3,
 'svc__gamma': 'scale',
 'svc__kernel': 'rbf',
 'svc__max_iter': -1,
 'svc__probability': False,
 'svc__random_state': None,
 'svc__shrinking': True,
 'svc__tol': 0.001,
 'svc__verbose': False}

from sklearn.model_selection import GridSearchCV

param_grid = {'svc__C': [0.1, 1.0, 10.0, 100., 1000.], 
              'svc__kernel': ['rbf'], 
              'svc__gamma': [0.001, 0.01, 0.1, 1.0, 10., 100.]}


validator = GridSearchCV(model, param_grid, cv=5)
validator.fit(X, y)
validator.best_params_

{'svc__C': 0.1, 'svc__gamma': 1.0, 'svc__kernel': 'rbf'}

fig, ax = plt.subplots(figsize=(4, 4), tight_layout=True)
plot_decision_boundary(validator, ax)

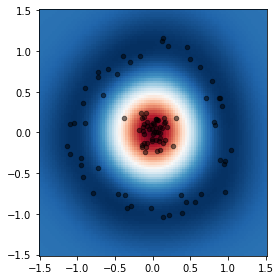
Ver también

Puede revisar ejemplos similares en la documentación de scikit-learn:

• SVM margin

• RBF parameters

• SVM kernels

También puede profundizar en las variantes del algoritmo SVM aquí.