1. Fundamentos de Aprendizaje Supervisado

1.1. Introducción

Dentro del aprendizaje de máquinas (machine learning) el aprendizaje supervisado es un paradigma o esquema en que se busca obtener una función

\[ f_{\theta}: \mathcal{X} \rightarrow \mathcal{Y}, \]

donde

• \(\mathcal{X}\) es el dominio de entrada al cual pertenecen nuestros datos o atributos

• \(\mathcal{Y}\) el dominio de salida al cual pertenece la variable objetivo que queremos predecir

• \(\theta\) es un vector de parámetros de la función o modelo

En esta unidad nos concentraremos en dos tipos de problemas o tareas, los cuales se describen a continuación:

Regresión

En esta tarea buscamos un modelo que asocie una entrada de \(m\) variables continuas a una salida de una variable continua

\[ f_{\theta}: \mathbb{R}^m \rightarrow \mathbb{R} \]

Típicamente se llaman variables independientes a las entradas y variables dependientes a la salida.

Algunos ejemplos de problemas de regresión:

• El flujo de tráfico de una calle en función de un feed de video

• La concentración de un químico aereo en función del valor del mismo en el pasado

• La ocurrencia de una llamarada solar en función del brillo y la cantidad de manchas en la corona del sol

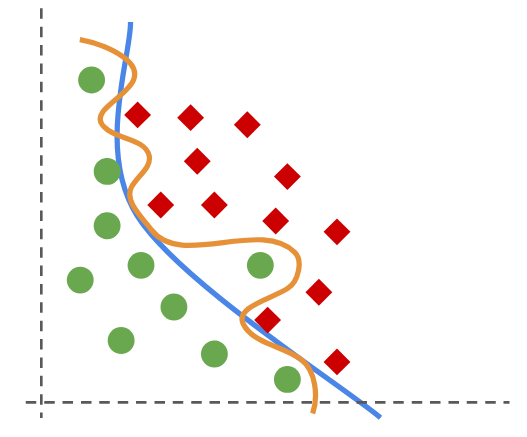
Clasificación

En esta tarea buscamos un modelo que retorne una entre \(K\) categorías para una entidad que se representa por \(m\) variables de entrada o atributos.

\[ f_{\theta}: \mathbb{R}^m \rightarrow \{1, 2, \ldots, K\} \]

Algunos ejemplos:

• Identificar si un correo electrónico es spam o no en base a descriptores de su contenido y sus metadatos

• Diagnóstico benigno o maligno en función de descriptores de las células de una biopsia por sospecha de cancer de mama

• Identificar la letra correspondiente a una imagen que muestra un gesto de lengua de señas

¿Puede reconocer cuales son las clases en cada uno de los problemas anteriores?

Otras tareas que se resuelven con machine learning

La siguiente lista tiene ejemplos de otras tareas de machine learning, supervisado, no supervisado y semi-supervisado, que no veremos en esta unidad.

• Machine Translation: El objetivo es convertir una secuencia de texto de un idioma a otro

• Imputación: El objetivo es rellenar valores faltantes en una base de datos

• Detección de anomalías: El objetivo es encontrar ejemplos atípicos, es decir que difieren en características al resto de la base de datos

• Denoising: El objetivo es retornar una versión de los datos de entrada con menos ruido

• Síntesis: El objetivo es generar nuevos ejemplos de texto, audio, o imágenes que se asemejan a los datos reales

• Clustering: El objetivo es agrupar los ejemplos según un criterio de similitud o densidad

1.2. Conceptos y definiciones

Entrenamiento

Los problemas de aprendizaje supervisado se resuelven “enseñándole” al modelo en base a ejemplos donde la respuesta correcta se conoce de antemano. Este proceso se denomina entrenamiento o ajuste del modelo.

Para entrenar necesitamos entonces un conjunto de \(N\) ejemplos:

\[ \{(x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N)\}, \]

donde cada ejemplo es una tupla que contiene

• \(x_i \in \mathcal{X}\): la entrada para el modelo (datos o atributos)

• \(y_i \in \mathcal{Y}\): la salida que el modelo debiera retornar (objetivo)

Nota

En problemas de clasificación, la variable objetivo suele llamarse etiqueta.

En modelos parámetricos como \(f_\theta\), entrenar corresponde a encontrar el valor de \(\theta\) con el cual se obtiene “el mejor” mapeo entre entrada y salida.

Para encontrar el mejor debemos definir primero un criterio (función de costo).

Función de costo

La función de costo, también llamada pérdida, mide el error de nuestro modelo sobre un conjunto de datos etiquetados.

Por ejemplo, para problemas de regresión, una función de costo muy común es la suma de errores cuadrados

\[ L(\theta) = \sum_{i=1}^N (f_\theta(x_i) - y_i)^2 \]

donde mientras más cerca a cero sea \(L(\theta)\), mejor es nuestro modelo (según este criterio).

En modelos parámetricos como \(f_\theta\), encontrar el mejor mapeo es equivalente a encontrar el valor de \(\theta\) que minimiza \(L(\theta)\), es decir el \(\theta\) óptimo.

Para encontrar el valor de \(\theta\) que minimiza el criterio necesitamos algoritmos de optimización.

Optimización

Para entrenar el modelo tenemos que resolver el siguiente problema:

\[ \min_\theta L(\theta) \]

Y las opciones que tenemos son:

• Evaluar \(L()\) con una estrategia de fuerza bruta. Esta opción es en general infactible.

• Aplicar técnicas analíticas, por ejemplo resolver \(\nabla_\theta L(\theta) = \vec 0\). Esta opción sólo puede aplicarse en algunos problemas.

• Usar técnicas numéricas iterativas, por ejemplo el método de Newton o gradiente descendente. Utilizaremos estas técnicas durante esta unidad.

Inferencia

Luego de entrenar y validar el modelo podemos utilizarlo para hacer inferir la variable objetivo \(y^*\) en datos nuevos \(x^*\), es decir fuera de los que se utilizaron para entrenar:

\[ y^* = f_\theta(x^*) \]

Importante

Este es el objetivo fundamental de machine learning: Aprender modelos complejos a partir de ejemplos para luego aplicarlos automaticamente sobre nuevos datos.

El siguiente diagrama ejemplifica este proceso y además compara machine learning con la programación tradicional:

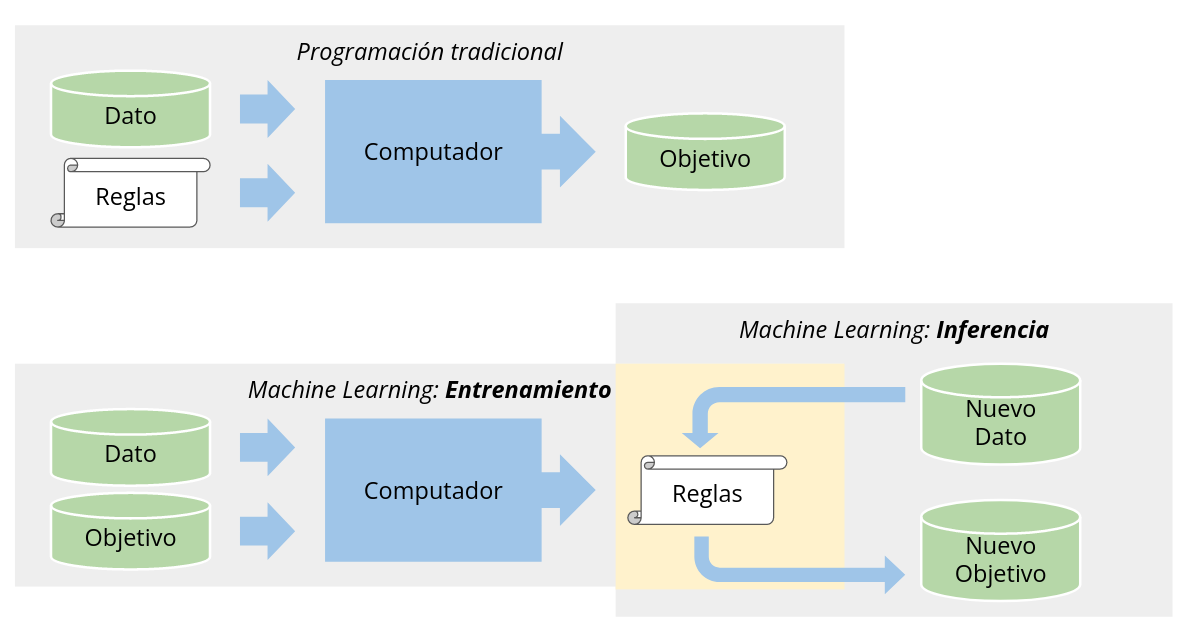
Generalización

Es la capacidad de un modelo de hacer buenas inferencias en datos que no fueron utilizados para ajustarlo (datos que no ha visto).

Nota

Para medir la capacidad de generalización se suele “esconder” una parte del conjunto de entrenamiento. Veremos este tipo de técnicas en detalle más adelante.

Representatividad

Es crítico que los datos que utilizemos representen adecuadamente el problema que queremos resolver. Idealmente, la distribución de los datos de entrenamiento no debiera diferir demasiado de los datos de prueba.

En caso de que esto ocurriera sería necesario reentrenar el modelo con nuevos datos que reflejen este cambio.

Sesgos

Un sesgo es una preferencia generalmente indeseada en un modelo. Muchas veces los sesgos del modelo son sesgos de los datos que utilizamos para entrenar. El más típico es el sesgo causado por clases desbalanceadas o exclusión de clases.

Ver también

Sin embargo esto puede ser más grave, por ejemplo sesgos raciales y de género, como muestra la siguiente breve presentación.