5. Evaluación de clasificadores

5.1. Métricas para clasificadores binarios

El regresor logístico retorna una predicción probabilística en el rango \([0, 1]\). Podemos convertir esta predicción en una decisión binaria seleccionando un umbral \(\mathcal{T}\) tal que

\[\begin{split} d_i = \begin{cases} 0, & \text{si } f_\theta(\vec x_i) < \mathcal{T} \\ 1, & \text{si } f_\theta(\vec x_i) \geq \mathcal{T} \end{cases} \end{split}\]

Nota

En un clasificador binario usar \(\mathcal{T}=0.5\) es equivalente al tomar el argumento máximo de la predicción probabilística.

Una vez seleccionado el umbral se puede contar la cantidad de

• True positives (TP): Ejemplos de clase (1) y clasificados como (1)

• True negative (TN): Ejemplos de clase (0) y clasificados como (0)

• False positives (FP): Ejemplos de clase (0) y clasificados como (1): Error tipo I

• False negative (FN): Ejemplos de clase (1) y clasificados como (0): Error tipo II

A partir de estas métricas se construye la tabla o matriz de confusión del clasificador

Predicho como/Etiqueta	Positivo	Negativo
Positivo:	TP	FP
Negativo:	FN	TN

Se puede estimar una matriz de confusión con scikit learn con

import numpy as np
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix


np.random.seed(20)
X, y = make_classification(n_features=2, n_classes=2, n_informative=2, 
                           n_redundant=0, n_clusters_per_class=1)


model = LogisticRegression(penalty=None)
model.fit(X, y)

for T in [0.1, 0.25, 0.5, 0.75, 0.9]:
    display(T, confusion_matrix(y_true=y, y_pred=model.predict_proba(X)[:, 1] > T))
    

0.1

array([[37, 13],
       [ 2, 48]])

0.25

array([[46,  4],
       [ 3, 47]])

0.5

array([[48,  2],
       [ 3, 47]])

0.75

array([[49,  1],
       [ 6, 44]])

0.9

array([[50,  0],
       [ 7, 43]])

Advertencia

Utilizar \(\mathcal{T}=0.5\) asume que el costo o riesgo de cometer un error tipo 1 es equivalente al de cometer un error tipo 2.

Nota

Modificando el umbral podemos ajustar el compromiso (trade-off) entre el error tipo 1 y el error tipo 2.

La matriz de confusión suele resumirse con las siguientes métricas:

True Positive Rate o Recall

La proporción de positivos correctamente clasificados respecto al total de positivos

\[ \text{TPR} = \frac{TP}{TP + FN} \]

False Positive Rate

La proporción de negativos incorrectamente clasificados respecto al total de negativos

\[ \text{FPR} = \frac{FP}{TN + FP} = 1 - \frac{TN}{TN + FP} \]

Precision o Pureza

La proporción de positivos correctamente clasificados respecto a todos los ejemplos clasificados como positivo

\[ \text{Precision} = \frac{TP}{TP + FP} \]

Accuracy

La proporción de ejemplos correctamente clasificados

\[ \text{Accuracy} = \frac{TP+TN}{TP + FP + FN+ TN} \]

F1-score

La media armónica entre Recall y Precision asumiendo igual ponderación

\[ \text{f1-score} = \frac{2 \cdot \text{Recall} \cdot \text{Precision}}{\text{Recall} + \text{Precision}} \]

Truco

Si las clases son desbalanceadas entonces f1-score es preferible ante accuracy

Podemos obtener estas métricas con scikit-learn utilizando

from sklearn.metrics import accuracy_score, classification_report

accuracy_score(y_true=y, y_pred=model.predict_proba(X)[:, 1] > T)

0.93

print(classification_report(y_true=y, y_pred=model.predict_proba(X)[:, 1] > T))

              precision    recall  f1-score   support

           0       0.88      1.00      0.93        50
           1       1.00      0.86      0.92        50

    accuracy                           0.93       100
   macro avg       0.94      0.93      0.93       100
weighted avg       0.94      0.93      0.93       100

5.2. Curvas de desempeño

Podemos estudiar gráficamente como cambian estas métricas en función del umbral utilizando una curva de desempeño. Típicamente se usan

• Curva ROC: TPR vs FPR

• Curva Precision vs Recall

En scikit-learn se pueden calcular con

from sklearn.metrics import roc_curve

fpr, tpr, th = roc_curve(y_true=y, y_score=model.predict_proba(X)[:, 1])

Que retorna un arreglo con las tasas de falsos positivos, verdaderos positivos y los umbrales (escogidos automáticamente) que se utilizaron para calcularlas.

Graficamos la curva ROC como:

%matplotlib inline
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(7, 4))
ax.plot(fpr, tpr, label='Modelo')
ax.plot([0, 0, 1], [0, 1, 1], 'k-.', alpha=0.5, label='Ideal')
ax.legend()
idx = np.argmin((th - 0.5)**2)
ax.scatter(fpr[idx], tpr[idx], s=100)
ax.set_xlabel('Tasa de Falsos positivos')
ax.set_ylabel('Tasa de Verdaderos Positivos (Recall)');

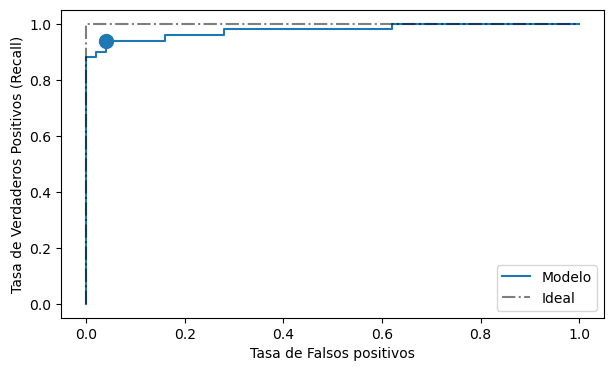
La curva ROC nos muestra el desempeño del modelo medido en función del umbral. Inspeccionado la curva ROC podemos seleccionar un punto de operación (umbral) que sea apropiado para nuestro problema

Nota

En general tendremos que se puede dismininuir el error tipo II (aumentar TPR) a costa de aumentar el error tipo I (aumentar FPR)

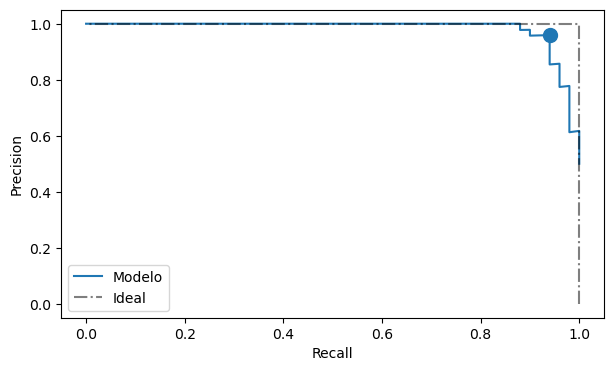
A continuación se calcula y muestra la curva de precision-recall, la cual es más apropiada que la anterior en el caso de clases desbalanceadas

from sklearn.metrics import precision_recall_curve

prec, rec, th = precision_recall_curve(y_true=y, probas_pred=model.predict_proba(X)[:, 1])

fig, ax = plt.subplots(figsize=(7, 4))
ax.plot(rec, prec, '-', label='Modelo');
ax.plot([1, 1, 0], [0, 1, 1], 'k-.', alpha=0.5, label='Ideal')
ax.legend()
idx = np.argmin((th - 0.5)**2)
ax.scatter(rec[idx], prec[idx], s=100)
ax.set_xlabel('Recall')
ax.set_ylabel('Precision');