4. Regresión Logística

Sea un dataset etiquetado una colección de \(N\) tuplas:

\[ D = \{(x_1, y_1), (x_2, y_2), \ldots (x_N, y_N)\} \]

donde la variable de entrada es \(x_i \in \mathbb{R}^M\) y la variable objetivo (etiqueta) es binaria \(y_i \in \{0, 1\}\).

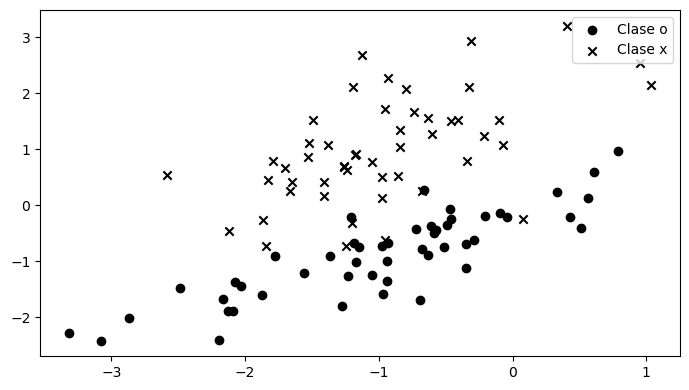
Por ejemplo un dataset con etiqueta binaria y con dos atributos \(M=2\) podría verse como la siguiente figura.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_classification

np.random.seed(20)
X, y = make_classification(n_features=2, n_classes=2, n_informative=2, 
                           n_redundant=0, n_clusters_per_class=1)

fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)
for y_, marker in zip(np.unique(y), ['o', 'x']):
    mask = y == y_
    ax.scatter(X[mask, 0], X[mask, 1], c='k', marker=marker, label=f'Clase {marker}')
ax.legend();

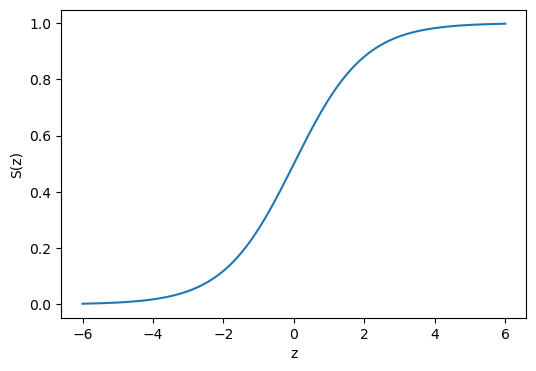
El regresor logístico es un clasificador binario lineal, es decir un modelo que separa el espacio de los datos en dos clases o categorías con un hiperplano.

El modelo se define matemáticamente como:

\[ f_\theta(x_i) = \mathcal{S} \left(\theta_0 + \sum_{j=1}^M \theta_j x_{ij}\right) \]

donde \(\theta_j\) son los parámetros del modelo, \(x_{ij}\) es el atributo \(j\) del dato \(i\) del dataset y

\[ \mathcal{S}(z) = \frac{1}{1+\exp(-z)}, \]

se conoce como función logística o sigmoide.

Nota

El regresor logístico es un ejemplo de una clase de modelos llamada regresor lineal generalizado que consisten en aplicar una función a la salida de un regresor lineal.

A continuación se muestra una gráfica de la función logística:

z = np.linspace(-6, 6, num=200)
sigmoid = lambda z: 1./(1+np.exp(-z))

fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(z, sigmoid(z))
ax.set_xlabel('z')
ax.set_ylabel('S(z)');

Luego

• \(f_\theta(x_i)\) puede interpretarse como la probabilidad de que \(x_i\) pertenezca a la clase “1”

• \(1-f_\theta(x_i)\) puede interpretarse como la probabilidad de que \(x_i\) pertenezca a la clase “0”

Podemos implementar este modelo en NumPy como:

def logistic_regressor(theta, x):
    z = theta[0] + np.dot(x, theta[1:])
    return sigmoid(z)

Consideremos un modelo con los siguientes parámetros

theta = np.array([-2.5, -3.3, 5.])

La predicción del modelo en el dataset mostrado al inicio de esta lección es:

def plot_prediction(ax, theta, plot_data=True, colorbar=False):
    xx1, xx2 = np.meshgrid(np.arange(-5, 4, 0.05), np.arange(-4, 4, 0.05))
    preds = logistic_regressor(theta, np.stack((xx1.ravel(),xx2.ravel())).T)
    artist = ax.contourf(xx1, xx2, preds.reshape(xx1.shape), cmap=plt.cm.RdBu)
    if colorbar:
        fig.colorbar(artist, ax=ax)
    if plot_data:
        for y_, marker in zip(np.unique(y), ['o', 'x']):
            mask = y == y_
            ax.scatter(X[mask, 0], X[mask, 1], c='k', marker=marker, label=f'Clase {marker}')
        ax.legend();

fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)
plot_prediction(ax, theta, colorbar=True)

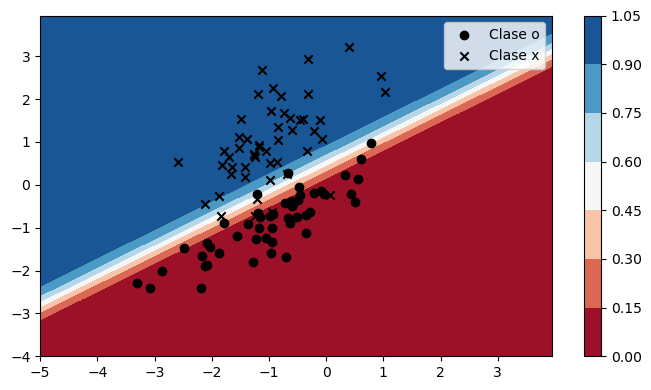
Los datos están bien separados por le clasificador, pero

¿Cómo se llega a estos valores para \(\theta\)?

Para ajustar o entrenar este modelo se utiliza la siguiente función de costo:

\[ L(\theta) = \sum_{i=1}^N -y_i \log( f_\theta(x_i) ) - (1-y_i) \log(1 - f_\theta(x_i)) \]

conocida como la Entropía Cruzada Binaria (binary cross entropy).

Podemos implementarla en NumPy como:

def bce_loss(theta, x, y, eps=1e-10):
    ypred = logistic_regressor(theta, x)
    return -np.sum(y*np.log(ypred+eps) + (1.-y)*np.log(1.-ypred+eps), axis=0)

Luego el gradiente de la función de costo es:

\[\begin{split} \begin{split} \frac{d}{d \theta_j} L(\theta) &= \sum_{i=1}^N \left(-\frac{y_i}{f_\theta(x_i)} + \frac{1-y_i}{1 - f_\theta( x_i)}\right) \frac{f_\theta( x_i)}{d\theta_j} \\ &= \begin{cases}-\sum_{i=1}^N (y_i - f_\theta( x_i)) x_{ij} &j>0\\ -\sum_{i=1}^N (y_i - f_\theta( x_i)) & j=0 \\ \end{cases} \end{split} \end{split}\]

Que en NumPy sería:

def grad_bce_loss(theta, x, y):
    ypred = logistic_regressor(theta, x)
    error = y - ypred
    D = np.ones(shape=(X.shape[0], 3))
    D[:, 1:] = x
    return -np.dot(error, D)

Advertencia

A diferencia de la regresión lineal, no podemos despejar analiticamente \(\theta\) debido a la no linealidad de \(f_\theta(\vec x_i)\).

Para entrenar este modelo se utilizan métodos de optimización iterativos, como los que se presentan a continuación.

4.1. Método de Newton y Gradiente descedente

Sea el valor actual del vector de parámetros \(\theta_t\)

Queremos encontrar el mejor “próximo valor” según nuestra función objetivo

\[ \theta_{t+1} = \theta_t + \Delta \theta \]

Consideremos la aproximación de Taylor de segundo orden de \(f\)

\[ f(\theta_{t} + \Delta \theta) \approx f(\theta_t) + \nabla f (\theta_t) \Delta \theta + \frac{1}{2} \Delta \theta^T H_f (\theta_t) \Delta \theta \]

Derivando en función de \(\Delta \theta\) e igualando a cero tenemos

\[\begin{split} \begin{split} \nabla f (\theta_t) + H_f (\theta_t) \Delta \theta &= 0 \\ \Delta \theta &= - [H_f (\theta_t)]^{-1}\nabla f (\theta_t) \\ \theta_{t+1} &= \theta_{t} - [H_f (\theta_t)]^{-1}\nabla f (\theta_t) \end{split} \end{split}\]

Se obtiene una regla iterativa en función del Gradiente y del Hessiano de \(L(\theta)\). El gradiente nos dice la dirección de máximo descenso y el hessiano la magnitud del paso

Cabe destacar que

• La solución depende de \(\theta_0\)

• Estamos asumiendo que la aproximación de segundo orden es “buena”

• Si nuestro modelo tiene \(M\) parámetros el Hessiano es de \(M\times M\), ¿Qué pasa si \(M\) es grande?

Si el Hessiano es prohibitivo podemos usar una aproximación de primer orden conocida como el método de gradiente descendente

\[ \theta_{t+1} = \theta_{t} - \eta \nabla f (\theta_t) \]

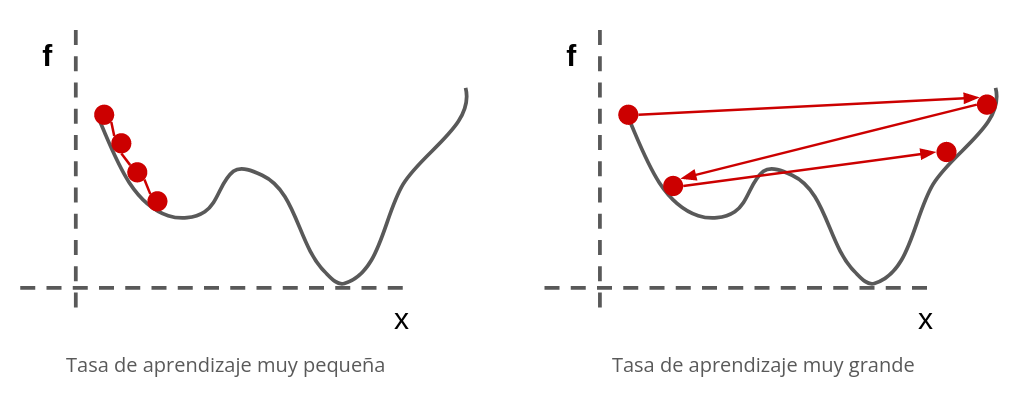
donde hemos reemplazado el Hessiano por una constante \(\eta\) llamado “paso” o “tasa de aprendizaje”

Advertencia

\(\eta\) es un hiperparámetro del modelo que debe ser calibrado cuidadosamente. Un valor muy alto vuelve el entrenamiento inestable mientas que un valor muy pequeño hará que el algoritmo tome un tiempo imprácticamente largo en llegar a la solución

Advertencia

El gradiente descedente converge a un punto estacionario. Si \(L(\theta)\) es no-convexo entonces el resultado podría corresponder a un mínimo local. Es importante verificar el resultado utilizando distintas valores de \(\theta_0\)

Utilicemos el gradiente descedente para entrenar el regresor logístico, en NumPy esto sería

def train(nepochs=10, lr=1e-2, rseed=None):
    np.random.seed(rseed)
    theta = np.zeros(shape=(nepochs+1, 3))
    theta[0] = np.random.randn(3)
    loss = np.zeros(shape=(nepochs,))
    for epoch in range(nepochs):
        loss[epoch] = bce_loss(theta[epoch], X, y)
        theta[epoch+1] = theta[epoch] - lr*grad_bce_loss(theta[epoch], X, y)
    return loss, theta

loss, theta = train(rseed=12345)

La evolución de la función de costo y el valor de los parámetros

fig, ax = plt.subplots(2, figsize=(7, 4), tight_layout=True, sharex=True)
ax[0].plot(loss)
ax[0].set_ylabel('BCE')
for param in theta.T:
    ax[1].plot(param)
ax[1].set_ylabel('Theta')
ax[1].set_xlabel('Epoca');

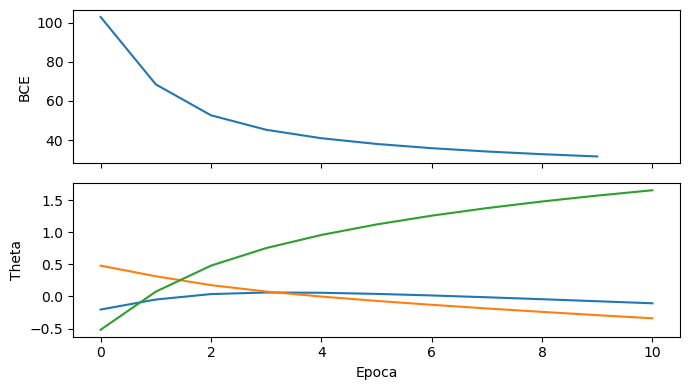
Y en este caso, con datos bidimensionales, podemos visualizar como se ajusta el plano separador época a época

fig, ax = plt.subplots(2, 5, figsize=(13, 5), sharex=True, sharey=True, tight_layout=True)
for k, ax_ in enumerate(ax.ravel()):
    ax_.axis('off')
    plot_prediction(ax_, theta[k, :])
    ax_.set_title(k)

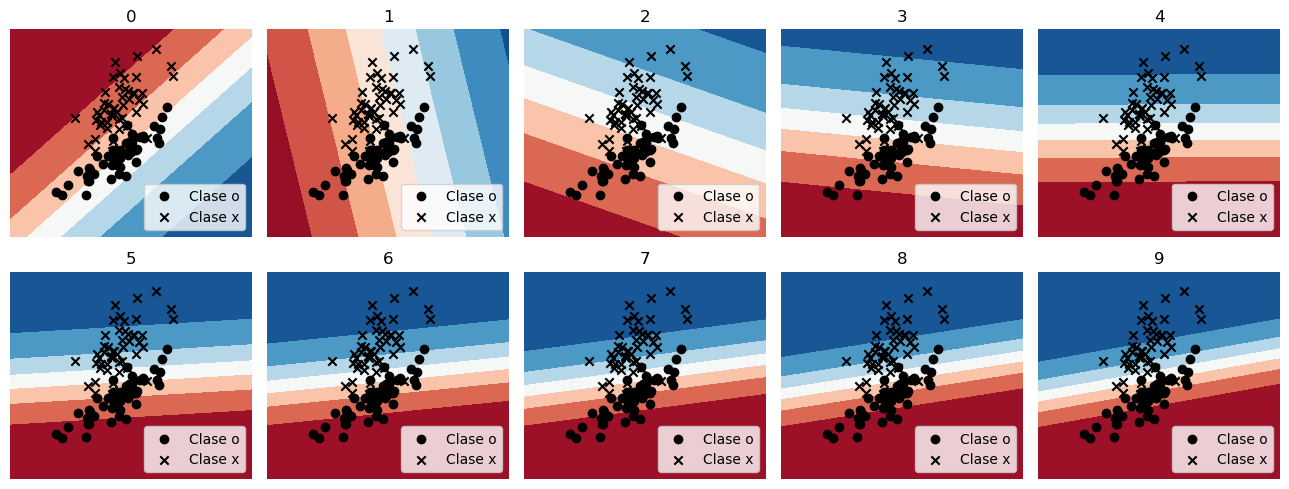
4.2. Regresor logístico en Scikit-Learn

En scikit-learn el regresor logístico está implementado en sklearn.linear_model.LogisticRegression

Los principales argumentos son

• penalty: Tipo de regularización, por ejemplo l2, l1 o None

• tol: Tolerancia para el criterio de detención

• solver: El algoritmo de optimización a utilizar, por defecto se usa L-BFGS un método quasi-Newton

• max_iter: Número máximo de épocas

• n_jobs: Núcleos de CPU a utilizar

Los principales métodos son

• fit(X, y): Entrenar el modelo con una base de datos X y etiquetas y

• predict_proba(X): Retorna las probabilidades de clase para los ejemplos X

• predict(X): Retorna la clase de mayor probabilidad de X

Y los principales atributos son

• intercept_: Corresponde a \(\theta_0\)

• coef_: Es un arreglo con \(\theta_j\) para \(j>0\)

Lo siguiente es equivalente a la implementación manual que se mostró anteriormente

from sklearn.linear_model import LogisticRegression

model = LogisticRegression(penalty=None)
model.fit(X, y)

print(model.intercept_, model.coef_)

[-2.44751183] [[-3.3470849   4.81780968]]

A continuación se muestra la diferencia entre predict y predict_proba para un dato ubicado en [1., 0.]

display(model.predict_proba(np.array([[1., 0.]])), 
        model.predict(np.array([[1., 0.]])))

array([[0.99696528, 0.00303472]])

array([0])

Nota

La predicción dura (predict) es equivalente al argumento máximo de la predicción probabilística (predict_proba).

np.allclose(np.argmax(model.predict_proba(X), axis=1), 
            model.predict(X))

True

A continuación se muestra graficamente la diferencia entre la predicción dura y la predicción probabilística:

y_soft = model.predict_proba(X)[:, 1]
y_hard = model.predict(X)

fig, ax = plt.subplots(1, 2, figsize=(9, 4), tight_layout=True)

for ax_, pred in zip(ax, [y_hard, y_soft]):
    for y_, marker in zip(np.unique(y), ['o', 'd']):
        mask = y == y_
        artist = ax_.scatter(X[mask, 0], X[mask, 1], c=pred[mask], marker=marker, s=100,
                             vmin=0, vmax=1, cmap=plt.cm.RdBu_r, edgecolors='k', linewidths=1)
    fig.colorbar(artist, ax=ax_);

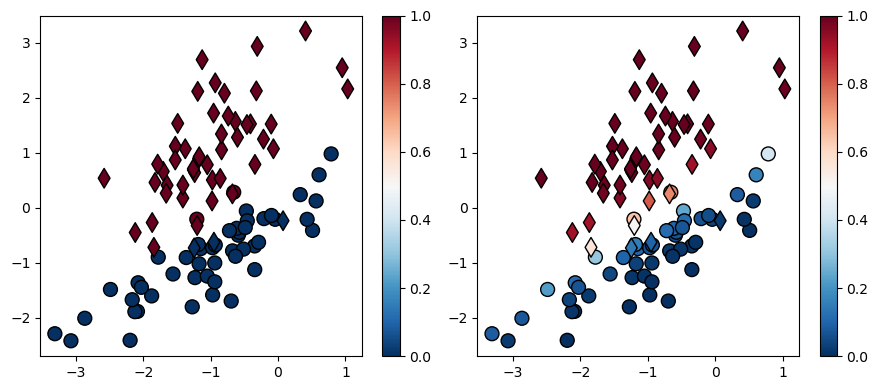
El tipo de símbolo corresponde a la etiqueta real mientras que el color corresponde a la etiqueta predicha.

Nota

En la próxima lección veremos como evaluar cuantitativamente el desempeño de un clasificador.