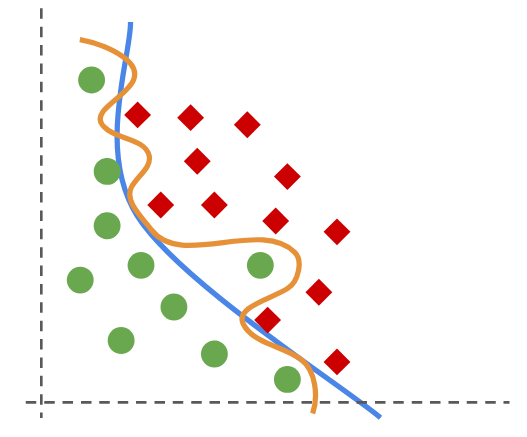
9. Ensambles secuenciales#

9.1. Boosting#

Boosting es una familia de algoritmos que buscan combinar estimadores (clasificadores o regresores) débiles de forma secuencial (cadena) para construir un estimador fuerte.

Estimador débil

Algoritmo que produce un resultado (al menos) levemente mejor que el azar

Estimador fuerte

Algoritmo que produce un resultado correcto en la mayoría de los ejemplos

Cualquier estimador débil puede ser mejorado (boosted) a un estimador fuerte

—Robert Shapire

El procedimiento general de un algoritmo de tipo boosting es:

  1. Entrenar un estimador débil con toda la distribución de datos

  2. Crear una nueva distribución que le da más peso a los errores del clasificador débil anterior

  3. Entrenar otro estimador débil en la nueva distribución

  4. Combinar los estimadores débiles y volver a 2

Estos pasos se muestran esquemáticamente en la siguiente figura para el caso particular de clasificación:

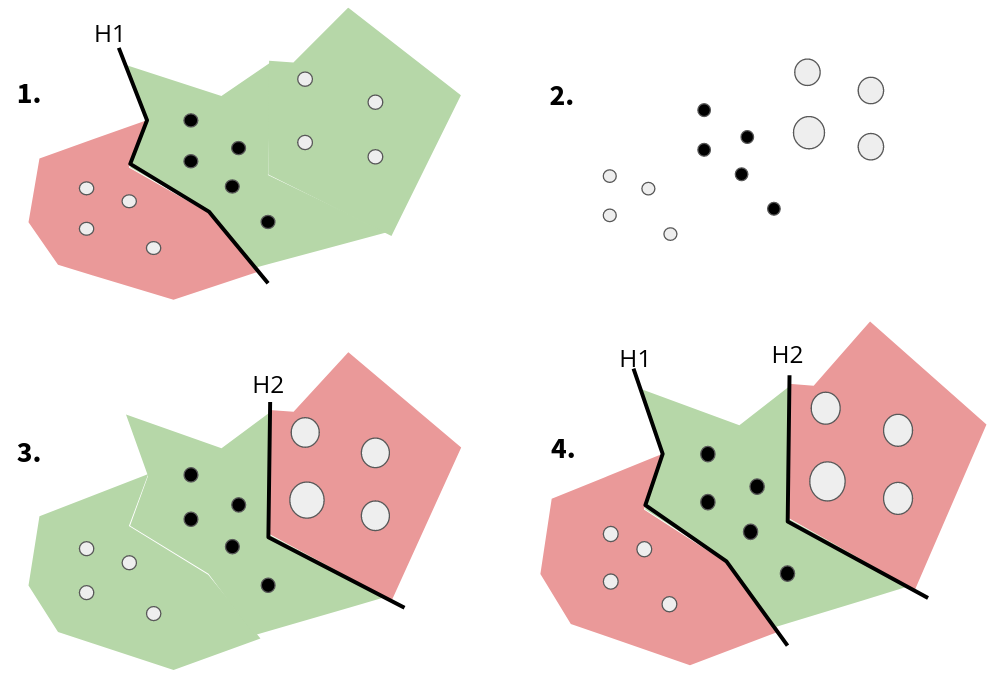
../../_images/boosting.png

Importante

El clasificador \(H_2\) se encarga de corregir los errores de \(H_1\). La combinación de \(H_1\) y \(H_2\) es el clasificador fuerte.

Matemáticamente:

Algorithm 9.1 (Algoritmo general de Boosting)

Entradas Un conjunto de datos \(\mathcal{D}\) y un número máximo de estimadores \(T\)

  1. Definir conjunto inicial \(D_{1} = D\)

  2. Para \(t = 1, \ldots, T\):

    1. Entrenar un estimador débil sobre \(D_t\)

    2. Evaluar el error del estimador débil

    3. Ponderar los ejemplos en base al error para crear \(D_{t+1}\)

  3. Combinar las salidas de los estimadores débiles

En esta lección utilizaremos árboles de decisión como estimador débil. Esto define los pasos de entrenamiento y evaluación del algoritmo anterior. Sólo resta definir como:

  • Crear \(D_{t+1}\)

  • Combinar los estimadores débiles

A continuación veremos como definen estos puntos dos algoritmos particulares de Boosting.

9.2. Adaptive Boosting (Adaboost)#

Adaboost es un algoritmo diseñado para clasificación binaria \(\{-1,1\}\) donde los clasificadores débiles se combinan linealmente como

\[ H_T(x) = \sum_{t=1}^T \alpha_t h_t(x) \]

donde la clase predicha se obtiene aplicando la función signo sobre \(H_T(x)\).

El ensamble se entrena minimizando la función de pérdida exponencial

\[\begin{split} \begin{split} \mathcal{L}(H_T) &= \sum_{i=1}^N \exp \left (-y_i H_T(x_i) \right) \\ &= \sum_{i=1}^N \exp \left (-y_i H_{T-1}(x_i) -y_i \alpha_T h_T(x_i)\right) \\ &= \sum_{i=1}^N w_i^{(T)}\exp \left (-y_i \alpha_T h_T(x_i)\right) \end{split} \end{split}\]

Nota

Para entrenar el último clasificador de la secuencia \(h_T\) podemos asumir \(w_i^{(T)}\) constante.

Dividiendo la función de costo en los casos bien y mal clasificados

\[\begin{split} \begin{split} \mathcal{L}(H_T) &= \sum_{i=1}^N w_i^{(T)}\exp \left (-y_i \alpha_T h_T(x_i)\right) \\ &= \sum_{h(x_i)y_i = 1} e^{-\alpha_T} w_i^{(T)} + \sum_{h(x_i)y_i \neq 1} e^{\alpha_T} w_i^{(T)} \end{split} \end{split}\]

y luego derivando en función de \(\alpha\) se tiene

\[ \alpha_t = \frac{1}{2} \log \left(\frac{1-\epsilon_t}{\epsilon_t} \right), \]

donde

\[ \epsilon_t = \frac{\sum_{i=1}^N w_i^{(T)} \mathbb{1}(h_t(x_i)\neq y_i)}{\sum_{i=1}^N w_i^{(T)}} \]

donde \(\mathbb{1}()\) es la función indicadora que es 1 si su argumento es cierto o 0 en caso contrario.

Con esto tenemos

Algorithm 9.2 (Algoritmo Adaptive Boosting)

Entradas Un conjunto de datos \(\mathcal{D}\) y un número máximo de estimadores \(T\)

  1. Inicializar los pesos \(w_i^{(1)} = 1/N\)

  2. Para \(t = 1, \ldots, T\):

    1. Entrenar un estimador débil \(h_t\) sobre los datos ponderados por \(w_i^{(t)}\)

    2. Calcular \(\alpha_t\)

    3. Actualizar los pesos \(w_i^{(t+1)} = w_i^{(t)} \exp (2 \alpha_t \mathbb{1}(h_t(x_i) \neq y_i))\)

El clasificador fuerte está totalmente definido por los clasificadores débiles \(h_t\) y los ponderadores \(\alpha_t\).

Nota

Los pesos de los datos se actualizan con los errores del último clasificador.

Importante

Los ensambles de tipo boosting reducen progresivamente el sesgo (error) agregando secuencialmente clasificadores débiles.

9.3. Gradient Boosting#

El algoritmo de gradient boosting combina el método de gradiente descendente con el algoritmo general de boosting. Es capaz de hacer tanto clasificación como regresión y puede usar cualquier función de pérdida que sea derivable.

Sea una función de costo sobre un dataset \((x_i, y_i)_{i=1,\ldots,N}\)

\[ \min \sum_{i=1}^N L(y_i, H_T(x_i)), \]

donde \(H_T\) es el estimador fuerte.

Por ejemplo, en un problema de regresión, este se define como

\[ H_T(x_i) = \sum_{t=1}^T h_t(x_i), \]

es decir una suma de “regresores” débiles.

En un problema de regresión se utiliza típicamente el error cuadrático medio como función de costo

\[ L(H_T(x_i), y_i) = \frac{1}{2} \left(y_i - H_T(x_i) \right)^2 \]

Supongamos que tenemos \(H_3 = h_1 + h_2 + h_3\) y deseamos agregar un nuevo estimador tal que

\[ H_4 = H_3 + h_4 \]

Nota

Los estimadores se agregan de uno por uno de forma greedy.

Agregar el nuevo estimador debería acercar al estimador fuerte a la etiqueta es decir

\[ H_3 + h_4 \approx y \]

Para lograr esto el nuevo estimador \(h_4\) se entrena minimizando el residuo \(y-H_3\)

\[ h_4 = \text{arg} \min_{h} \sum_{i=1}^N L(h(x_i), y_i - H_3(x_i)) \]

donde el residuo está relacionado a

\[ \frac{dL(H_3(x_i), y_i)}{dH_3(x_i)} = H_3(x_i) - y_i \]

Nota

Si utilizamos el error cuadrático, entonces los residuos son equivalentes al negativo del gradiente, esta es la razón del nombre del algoritmo.

Para reducir el sobreajuste del ensamble (regularización) se agrega típicamente

\[ H_{t+1} = H_t + \nu h_t \]

una constate \(\nu\) denominada tasa de aprendizaje. Esto disminuye la contribución de cada estimador débil (enlentece el entrenamiento).

Nota

En general una tasa de aprendizaje pequeña requerirá una mayor cantidad de clasificadores débiles. La ventaja de una tasa pequeña es que está relacionada a menores errores en el conjunto de test .

Para problemas de clasificación con \(K\) clases se suele utilizar la siguiente función de costo, llamada generalmente logarithmic loss o log loss

\[ L(y_i, x_i) = \sum_{k=1}^K y_{ik} \log p_k (x_i) \]

donde \(y_i\) es un vector de largo K de tipo one-hot y \(H(x)\) retorna también un vector de largo \(K\) que se normaliza como

\[ p_k(x) = \frac{e^{H^{(k)}(x)}}{ \sum_{k=1}^K e^{H^{(k)}(x)} } \]

tal que cada componente este en el rango \([0,1]\) y que además los \(K\) sumen uno.

9.4. Implementación en scikit-learn#

El módulo ensemble de scikit-learn tiene implementaciones de Gradient Boosting para problemas de clasificación y regresión. Nos enfocaremos en la primera.

Los principales argumentos de GradientBoostingClassifier son:

  • loss: La función de costo. Las opciones son 'log_loss' (dependiendo de su versión de scikit-learn) o 'exponential'

  • n_estimators: Cantidad de clasificadores débiles

  • learning_rate: Tasa de aprendizaje (no-negativo)

  • subsample: Booleano que indica si cada clasificador débil utiliza el dataset completo o una submuestra

Nota

Si se utiliza loss='exponential' el algoritmo se vuelve equivalente a AdaBoost (sólo para clasificación binaria).

También recibe argumentos relacionados a los clasificadores débiles (árboles), entre ellos:

  • max_depth: Profundidad máxima de los árboles

  • min_samples_split: Número mínimo de muestras para permitir un split

El objeto tiene implementados los métodos usuales fit, predict, predict_proba y decision_function.

Adicionalmente cuenta con staged_predict, staged_predict_proba y staged_decision_function, que retornan las predicciones de los clasificadores débiles individuales.

import sklearn
print(sklearn.__version__)

1.2.2

Ejemplo:

Entrenamiento de ensamble gradient boosting para clasificación de vino

import numpy as np
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split

data_struct = load_wine()
X = data_struct.data
y = data_struct.target
X_names = data_struct.feature_names

np.random.seed(0)
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, test_size=0.3)

Se realiza una validación cruzada buscando los mejores hiperparámetros del modelo:

%%time

from sklearn.ensemble import GradientBoostingClassifier
from sklearn.model_selection import GridSearchCV

params = {'learning_rate': [0.1, 0.2, 0.5], 
          'max_depth': [1, 5, 10, 20],
          'n_estimators': [1, 10, 20, 50, 100]}

model = GradientBoostingClassifier(loss='log_loss')
validator = GridSearchCV(model, params, cv=3, refit=True)
validator.fit(X_train, y_train)

CPU times: user 24 s, sys: 6.92 ms, total: 24 s
Wall time: 24.1 s

GridSearchCV(cv=3, estimator=GradientBoostingClassifier(),
             param_grid={'learning_rate': [0.1, 0.2, 0.5],
                         'max_depth': [1, 5, 10, 20],
                         'n_estimators': [1, 10, 20, 50, 100]})
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Los mejores modelos de acuerdo a la validación cruzada son:

import pandas as pd
columns = ["param_learning_rate", "param_max_depth", "param_n_estimators", 
           "mean_test_score", "std_test_score", "rank_test_score"]
pd.DataFrame(validator.cv_results_)[columns].sort_values(by="rank_test_score").head(5)
param_learning_rate param_max_depth param_n_estimators mean_test_score std_test_score rank_test_score
24 0.2 1 100 0.959930 0.022174 1
41 0.5 1 10 0.959930 0.022174 1
21 0.2 1 10 0.951994 0.033398 3
42 0.5 1 20 0.951994 0.033398 3
23 0.2 1 50 0.944057 0.044622 5

En este caso hay varios modelos que obtuvieron el primer lugar en términos de accuracy promedio

GridSearchCV retorna arbitrariamente el primero en orden de ejecución:

validator.best_params_

{'learning_rate': 0.2, 'max_depth': 1, 'n_estimators': 100}

Nota

Boosting funciona bien con árboles poco profundos. Los árboles de poca profundidad suelen tener alto sesgo y baja varianza.

El resultado de predicción en el conjunto de test es:

from sklearn.metrics import classification_report

best_gb = validator.best_estimator_
print(classification_report(y_test, best_gb.predict(X_test)))

              precision    recall  f1-score   support

           0       0.95      1.00      0.97        19
           1       1.00      0.95      0.98        22
           2       1.00      1.00      1.00        13

    accuracy                           0.98        54
   macro avg       0.98      0.98      0.98        54
weighted avg       0.98      0.98      0.98        54

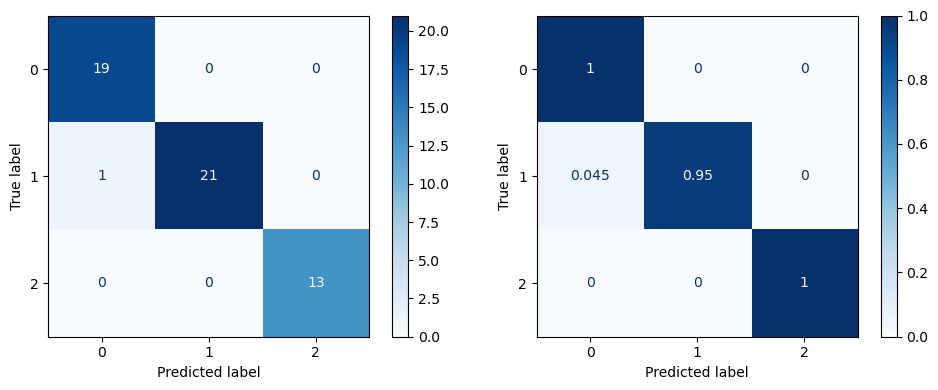
%matplotlib inline
import matplotlib.pyplot as plt
from sklearn.metrics import ConfusionMatrixDisplay

fig, ax = plt.subplots(1, 2, figsize=(10, 4), tight_layout=True)

ConfusionMatrixDisplay.from_predictions(y_test, validator.predict(X_test), normalize=None,
                                        ax=ax[0], cmap='Blues', colorbar=True);

ConfusionMatrixDisplay.from_predictions(y_test, validator.predict(X_test), normalize='true',
                                        ax=ax[1], cmap='Blues', colorbar=True);
../../_images/8fd002770adb9481663f8e517ce8890515c92e777d812f0e6904b229d52a3163.png

Ver también

Otros algoritmos de Boosting con árboles de decisión extremadamente competitivos:

Estos implementan estrategias para mejorar la eficiencia y realizar cálculos paralelos/distribuidos.