22. Q-learning con estado continuo#
22.1. Ambiente: Carro con péndulo#
En el ambiente CartPole existe un carro con un poste que se balancea sobre él.

El objetivo es aplicar fuerzas con tal de balancear el poste el mayor tiempo posible. Inicialmente el poste está derecho. El episodio termina si:
Si el poste se inclina más de 15 grados en cualquier dirección
Si el carro se aleja más de 2.4 unidades del centro
Se superan los 500 pasos
EL siguiente bloque ejecuta el ambiente con un policy aleatorio en una ventana externa.
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
import gymnasium as gym
env = gym.make("CartPole-v1", render_mode="human")
env.reset()
terminated, truncated = False, False
states = []
for k in range(200):
if terminated or truncated:
break
a = env.action_space.sample()
s, r, terminated, truncated, info = env.step(a)
states.append(s)
env.render()
Podemos cerrar la ventana del ambiente con:
env.close()
Acciones
Existen dos acciones:
Aplicar una unidad de fuerza hacia la izquierda
Aplicar una unidad de fuerza hacia derecha
Es decir el espacio de acciones es discreto.
# Tipo de las acciones
display(env.action_space)
# Cantidad de acciones
display(env.action_space.n)
Discrete(2)
2
Estados
El espacio de estados tiene 4 variables:
Posición del carro
Velocidad del carro
Ángulo del poste (radianes)
Velocidad angular del poste
El espacio de estado es continuo. Recuperamos el valor del estado con:
env.state
(-0.10337269475852862,
-0.9857585815994362,
0.21049700813357136,
1.7231934431646523)
Podemos también recuperar las cotas de las variables de estado
# Si está acotado o no
display(env.observation_space.is_bounded())
# Cota inferior
display(env.observation_space.low)
# Cota superior
display(env.observation_space.high)
True
array([-4.8000002e+00, -3.4028235e+38, -4.1887903e-01, -3.4028235e+38],
dtype=float32)
array([4.8000002e+00, 3.4028235e+38, 4.1887903e-01, 3.4028235e+38],
dtype=float32)
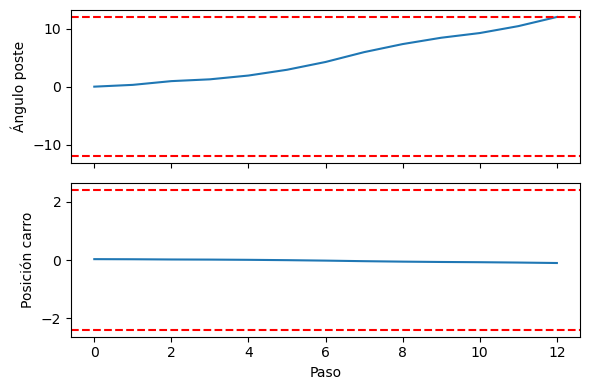
fig, ax = plt.subplots(2, figsize=(6, 4), tight_layout=True, sharex=True)
ax[0].plot(np.array(states)[:, 2]*180/np.pi)
ax[0].axhline(12, ls='--', c='r')
ax[0].axhline(-12, ls='--', c='r')
ax[0].set_ylabel('Ángulo poste')
ax[1].plot(np.array(states)[:, 0])
ax[1].axhline(2.4, ls='--', c='r')
ax[1].axhline(-2.4, ls='--', c='r')
ax[1].set_ylabel('Posición carro')
ax[1].set_xlabel('Paso');
22.2. Discretización de estados#
¿Es posible utilizar Q-learning si el espacio es continuo?
Si, pero necesitamos discretizar el estado para poder construir nuestra tabla Q
Debemos decidir:
el rango de las variables
la resolución de las variables
En este caso particular:
La posición del carro y el ángulo de la barra están acotadas
La velocidad del carro y la velocidad angular de la barra no están acotadas
En base a esto creamos una función auxiliar que discretiza el espacio de estados
import numpy as np
def create_bin_limits(bounds, n_bins):
return np.linspace(bounds[0], bounds[1], n_bins-1)
#n_bins = (100, 100, 100, 100)
n_bins = (10, 10, 10, 10)
#n_bins = (1, 1, 10, 10)
# bins for x
x_limits = create_bin_limits((-2.4, 2.4), n_bins[0])
display(x_limits)
# bins for v
v_limits = create_bin_limits((-2.4, 2.4), n_bins[1])
display(v_limits)
# bins for t
t_limits = create_bin_limits((-15*np.pi/180, 15*np.pi/180), n_bins[2])
display(t_limits*180/np.pi)
# bins for w
w_limits = create_bin_limits((-50*np.pi/180, 50*np.pi/180), n_bins[3])
display(w_limits*180/np.pi)
print(f"Cantidad de estados {np.prod(np.array(n_bins))}")
# Función para obtener estado discreto
def get_state(state):
x, v, t, w = state
x_state = np.searchsorted(x_limits, x)
v_state = np.searchsorted(v_limits, v)
t_state = np.searchsorted(t_limits, t)
w_state = np.searchsorted(w_limits, w)
return (x_state, v_state, t_state, w_state)
array([-2.4, -1.8, -1.2, -0.6, 0. , 0.6, 1.2, 1.8, 2.4])
array([-2.4, -1.8, -1.2, -0.6, 0. , 0.6, 1.2, 1.8, 2.4])
array([-15. , -11.25, -7.5 , -3.75, 0. , 3.75, 7.5 , 11.25,
15. ])
array([-50. , -37.5, -25. , -12.5, 0. , 12.5, 25. , 37.5, 50. ])
Cantidad de estados 10000
Nota
El tamaño del espacio de estados crece muy rápido con la cantidad de bines
Las variables de estados no tienen que tener la misma resolución
Los bines no tienen porque ser del mismo tamaño
22.3. Entrenamiento con Epsilon-Greedy Q-Learning#
%%time
env = gym.make("CartPole-v1", render_mode="rgb_array")
Q = np.zeros(shape=(n_bins[0], n_bins[1], n_bins[2], n_bins[3], env.action_space.n))
diagnostics = {'rewards': [], 'episode_length': []}
alpha, gamma, episodes = 0.1, 0.999, 10_000
epsilon_init, epsilon_end, epsilon_rate = 1.0, 0.01, 1e-3
epsilon = lambda episode : epsilon_end + (epsilon_init - epsilon_end) * np.exp(-epsilon_rate*episode)
#epsilon = lambda episode : 0
n_evaluations = 10
np.random.seed(1234)
for episode in range(episodes):
env.reset()
terminated, truncated = False, False
while not terminated and not truncated:
s_current = get_state(env.state)
if not np.random.binomial(1, p=1.-epsilon(episode)) and ~np.all(Q[s_current]==0):
a = np.argmax(Q[s_current])
else:
a = env.action_space.sample()
s, r, terminated, truncated, info = env.step(a)
s_future = get_state(s)
Q[s_current][a] += alpha*(r + gamma*np.max(Q[s_future]) - Q[s_current][a])
if np.mod(episode+1, 100) == 0:
diagnostics['rewards'].append(np.zeros(shape=(n_evaluations,)))
diagnostics['episode_length'].append(np.zeros(shape=(n_evaluations,)))
for k in range(n_evaluations):
env.reset()
terminated, truncated = False, False
episode_length, episode_reward = 0, 0.0
while not terminated and not truncated:
s_current = get_state(env.state)
a = np.argmax(Q[s_current])
s_future, r, terminated, truncated, info = env.step(a)
episode_length += 1
episode_reward += r
diagnostics['rewards'][-1][k] = episode_reward
diagnostics['episode_length'][-1][k] = episode_length
CPU times: user 35.4 s, sys: 19.9 ms, total: 35.4 s
Wall time: 35.6 s
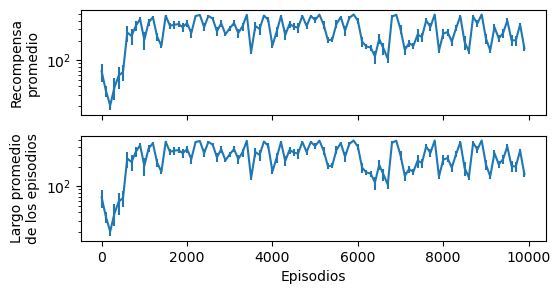
fig, ax = plt.subplots(2, figsize=(6, 3), sharex=True)
episodes = np.arange((episode+1)//100)*100
ax[0].errorbar(episodes,
np.array(diagnostics['rewards']).mean(axis=1),
np.array(diagnostics['rewards']).std(axis=1)/np.sqrt(n_evaluations));
ax[0].set_ylabel('Recompensa\npromedio');
ax[1].errorbar(episodes,
np.array(diagnostics['episode_length']).mean(axis=1),
np.array(diagnostics['episode_length']).std(axis=1)/np.sqrt(n_evaluations));
ax[1].set_xlabel('Episodios')
ax[1].set_ylabel('Largo promedio\nde los episodios');
ax[0].set_yscale('log')
ax[1].set_yscale('log')
Probando nuestro agente
env = gym.make("CartPole-v1", render_mode="human")
env.reset()
states = []
for k in range(500):
env.render()
states.append(env.state)
s_current = get_state(env.state)
a = np.argmax(Q[s_current])
s_future, r, terminated, truncated, info = env.step(a)
if terminated:
break
display(terminated, k)
True
341
env.close()
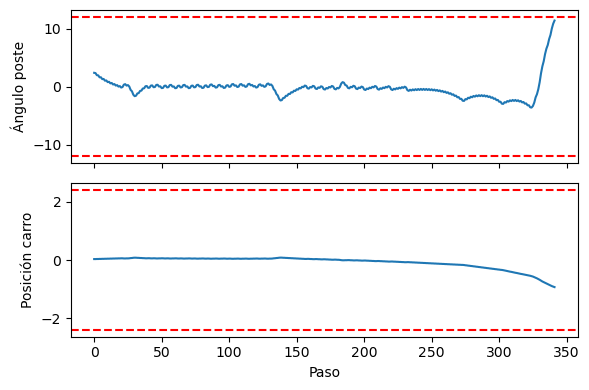
Seguimiento de los estados durante un episodio
fig, ax = plt.subplots(2, figsize=(6, 4), tight_layout=True, sharex=True)
ax[0].plot(np.array(states)[:, 2]*180/np.pi)
ax[0].axhline(12, ls='--', c='r')
ax[0].axhline(-12, ls='--', c='r')
ax[0].set_ylabel('Ángulo poste')
ax[1].plot(np.array(states)[:, 0])
ax[1].axhline(2.4, ls='--', c='r')
ax[1].axhline(-2.4, ls='--', c='r')
ax[1].set_ylabel('Posición carro')
ax[1].set_xlabel('Paso');
Actividad formativa: Estudie la influencia de la resolución de los estados.
Estudie que ocurre usando 100 bines en lugar de 10
Luego estudie que ocurre cuando se usa 1 sólo bin para la posición y para la velocidad
22.4. Desafios en RL#
Formular adecuadamente los estados, acciones y recompensa
Controlar el balance entre exploración y explotación
Obtener datos que representen la tarea