14. Introducción al procesamiento digital de imágenes#
14.1. Imágenes digitales#
Una imagen es una colección de píxeles ordenados. En estándar RGB cada pixel corresponde a 3 valores enteros de 8 bit (256 niveles). Combinándolos formamos colores (aproximadamente 16.7M).
Otra codificación usual para los píxeles consiste en usar un número entre cero y uno para cada canal (color). El estándar RGBA añade un canal que representa la opacidad. Las imágenes en escala de grises y sin opacidad se pueden representar usando un canal.
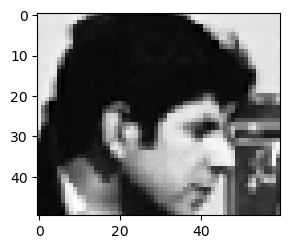
A continuación se muestra una imagen transformada a escala de grises mediante una combinación de sus canales de color:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
img = plt.imread('img/cameraman.png')
def to_grayscale(img):
return np.dot(img[:, :, :3],
np.array([0.2989, 0.587, 0.114]))
img_bw = to_grayscale(img)
display(img_bw.shape)
display(img_bw.dtype)
plt.figure(figsize=(4, 4), tight_layout=True)
plt.imshow(img_bw, cmap=plt.cm.Greys_r);
(327, 326)
dtype('float64')

Para nuestros sistemas digitales una imagen es una arreglo multidimensional y podemos operarlo como tal.
¿A qué corresponde este segmento del arreglo?
subimg = np.copy(img_bw[50:100, 120:180])
display(subimg)
array([[0.72541766, 0.72933884, 0.72933884, ..., 0.72149649, 0.71757531,
0.71365413],
[0.72541766, 0.73326002, 0.73326002, ..., 0.71757531, 0.71365413,
0.71365413],
[0.73718119, 0.72541766, 0.72541766, ..., 0.71757531, 0.70189061,
0.72541766],
...,
[0.03529059, 0.03136941, 0.03136941, ..., 0.15684706, 0.14116236,
0.18821647],
[0.03529059, 0.02744824, 0.02744824, ..., 0.15684706, 0.14116236,
0.23527059],
[0.03529059, 0.03136941, 0.02352706, ..., 0.15292589, 0.13332001,
0.27448237]])
plt.figure(figsize=(3, 3), tight_layout=True)
plt.imshow(subimg, cmap=plt.cm.Greys_r);
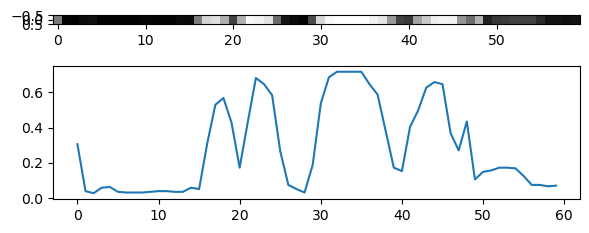
¿Y este segmento?
fig, ax = plt.subplots(2, 1, figsize=(6, 3), tight_layout=True)
ax[1].plot(subimg[30, :])
ax[0].imshow(subimg[30:31, :], cmap=plt.cm.Greys_r);
14.2. Convolución y correlación cruzada discreta#
Una herramienta clásica de procesamiento digital de señales es la convolución. La operación de convolución entre dos señales unidimensionales discretas es
y la operación de correlación cruzada es
Nota
Para ambas operaciones el resultado es una nueva señal que también depende de \(n\).
Por ejemplo el elemento \(0\) de \(f\star g\) se calcula como
f[0] g[0] + f[1] g[1] + f[2] g[2] + ...
Luego el elemento \(1\) sería
f[0] g[1] + f[1] g[2] + f[2] g[3] + ...
14.3. Filtrado de imágenes con convoluciones#
Se puede extender el concepto de convolución a dos dimensiones
donde \(n_1\) es el índice de las filas y \(n_2\) es el índice de las columnas
Nota
La convolución entre dos imágenes es una nueva imagen
La imagen \(I_1\) es la entrada
La imagen \(I_2\) se denomina filtro o kernel de la convolución
La imagen resultante es la imagen filtrada
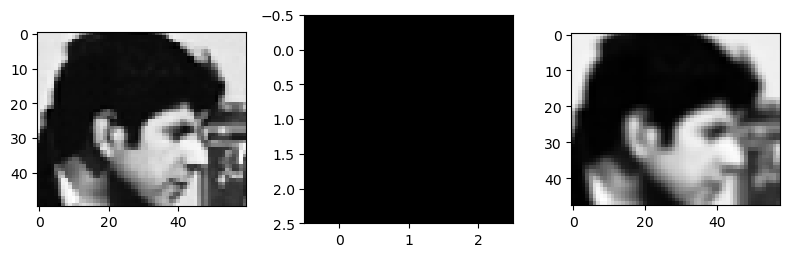
Filtro pasa-bajo
Suaviza, elimina los detalles
import scipy.signal
D = 3
filt = np.ones(shape=(D, D))
display(filt)
img_res = scipy.signal.correlate2d(subimg, filt/np.sum(filt), mode='valid')
fig, ax = plt.subplots(1, 3, figsize=(8, 3), tight_layout=True)
ax[0].imshow(subimg, cmap=plt.cm.Greys_r)
ax[1].imshow(filt, cmap=plt.cm.Greys_r)
ax[2].imshow(img_res, cmap=plt.cm.Greys_r);
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
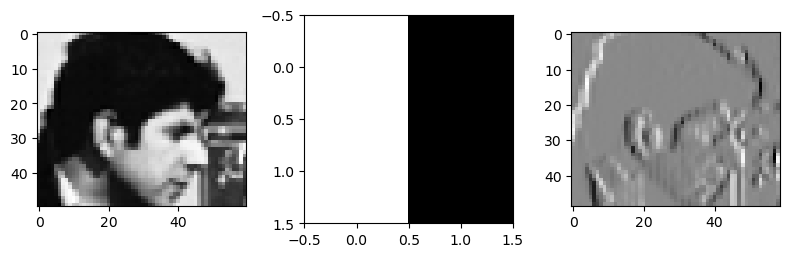
Filtro pasa-alto
Resalta los cambios bruscos, elimina las partes “planas”
filt = np.array([[1., -1.]]*2)
display(filt)
img_res = scipy.signal.correlate2d(subimg, filt, mode='valid')
fig, ax = plt.subplots(1, 3, figsize=(8, 3), tight_layout=True)
ax[0].imshow(subimg, cmap=plt.cm.Greys_r)
ax[1].imshow(filt, cmap=plt.cm.Greys_r)
ax[2].imshow(img_res, cmap=plt.cm.Greys_r);
array([[ 1., -1.],
[ 1., -1.]])
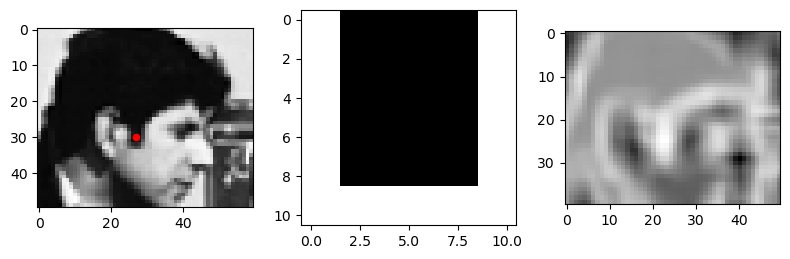
¿Detector de patillas?
Detecta patillas de fotógrafos mirando al horizonte.
filt = np.ones(shape=(11, 11))
filt[:9, 2:9] = 0
display(filt)
array([[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])
img_res = scipy.signal.correlate2d(subimg, filt-np.mean(filt), mode='valid')
fig, ax = plt.subplots(1, 3, figsize=(8, 3), tight_layout=True)
ax[0].imshow(subimg, cmap=plt.cm.Greys_r)
maxloc = np.unravel_index(np.argmax(img_res), shape=img_res.shape)
ax[0].scatter(maxloc[1]+filt.shape[0]//2, maxloc[0]+filt.shape[1]//2, c='r', s=20)
ax[1].imshow(filt, cmap=plt.cm.Greys_r)
ax[2].imshow(img_res, cmap=plt.cm.Greys_r);
En realidad el filtro se activa con cualquier cosa con forma de “U”.
Importante
Si modificamos los píxeles del kernel podemos crear un filtro para detectar objetos arbitrarios.
Esta es la base de las redes neuronales convolucionales
14.4. Visión computacional#
La visión computacional es un campo de investigación que busca que los computadores sean capaces de “comprender” el contenido presente en imágenes digitales y video. Podemos resumir su objetivo como:
Automatizar tareas realizas por el sistema visual humano
Algunos ejemplos de tareas de visión computacional:
Clasificación: ¿A qué categoría corresponde el patrón en la imagen?
Detección, Localización y Segmentación: ¿Dónde está el patrón en la imagen?
Ejemplos de aplicaciones
Herramientas
Procesamiento digital de imágenes
Optimización, Estadística
Machine learning y en particular Redes Neuronales Convolucionales
Desafíos
Algoritmos invariantes a los cambios de Iluminación
Algoritmos invariantes a los cambios de escala y perspectiva (deformación)
Algoritmos robustos contra la oclusión