13. Entrenamiento de redes neuronales con PyTorch#
13.1. Funciones de costo y optimizadores#
Para entrenar una red neuronal debemos definir
Una función de costo: Aquello que vamos a minimizar
Un algoritmo de optimización: De que forma vamos a minimizar
Las funciones de costo están implementadas torch.nn, a continuación revisaremos las dos más comunes. La clase MSELoss representa el error cuadrático medio. Se utiliza en problemas de regresión (etiqueta con valores reales) y se define como
donde \(y\) es la etiqueta (vector con D dimensiones) e \(\hat y\) es la predicción del modelo
Nota
Cuando entrenamos con esta función de costo debemos asegurarnos de que el modelo tenga tantas unidades de salida como dimensiones tenga la etiqueta
La clase CrossEntropyLoss representa la entropía cruzada. Esta función de costo se utiliza en problemas de clasificación de \(C\) clases y se define como
donde \(y_c \in \{0,1\}\), \(\hat y_c \in [0,1]\) y \(\sum_{c=1}^C \hat y_c = 1\)
Nota
Cuando entrenamos con esta función de costo debemos asegurarnos de que el modelo tenga tantas unidades de salida como clases tenga el problema.
Advertencia
La implementación de entropía cruzada de torch espera que las etiquetas \(y\) estén en formato categórico, es decir como un entero con valor \(0, 1, 2, \ldots, C-1\). Adicionalmente espera las predicciones \(\hat y\) estén en formato logits (números reales sin activación)
Luego de crear una instancia de estas clases las podemos llamar con una función. Por ejemplo si queremos calcular el error medio cuadrático entre dos tensores:
criterion = torch.nn.MSELoss(reduction='mean')
loss = criterion(output, target)
Nota
También podemos crear nuestra propia función de costo. Por ejemplo podríamos lograr lo mismo que MSELoss habiendo definido criterion = lambda ypred, y : (y-ypred).pow(2).mean()
Los algoritmos de optimización están implementados en el módulo torch.optim. Hoy en día los más utilizados son
Optimizador |
Descripción |
|---|---|
Gradiente descedente estocástico con momentum |
|
Gradiente descedente con tasa de aprendizaje adaptiva |
Para crear un objeto optimizar debemos entregar como argumento los parámetros del modelo y las argumetnos específicos del optimizar, por ejemplo para SGD:
optimizer = torch.optim.SGD(model.parameters(), lr=1e-3, momentum=0, weight_decay=0)
donde:
lrEs la tasa de aprendizaje. Debe ser un valor pequeño para no desestabilizar el entrenamiento, pero no tan pequeño para enlentencerlo demasiadomomentumes la tasa de momentum. Podemos utilizar un valor mayor que cero para evitar estancamiento en mínimos localesweight_decaycontrola la regularización (norma L2) de los parámetros. Podemos utilizar un valor mayor que cero para evitar sobreajuste
Una vez creado podemos llamar su función principal step() la cual realiza una actualización de parámetros de acuerdo a las derivadas calculadas con loss.backward()
13.2. Ajustando un modelo paso a paso#
Consideremos el siguiente dataset \(X\) con etiqueta \(Y\). El dataset tiene cuatro ejemplos separados en dos clases. Los ejemplos tienen cada uno dos atributos.
Utilizaremos CrossEntropyLoss para entrenar por lo tanto utilizamos dos unidades de salida
import torch
import torch.nn as nn
X = torch.tensor([[-1.0, -1.0],
[-1.0, 1.0],
[1.0, -1.0],
[1.0, 1.0]])
Y = torch.tensor([0, 0, 0, 1])
n_features = X.shape[1]
n_classes = len(Y.unique())
n_hidden = 3
model = nn.Sequential(nn.Linear(n_features, n_hidden),
nn.Sigmoid(),
nn.Linear(n_hidden, n_classes))
criterion = torch.nn.CrossEntropyLoss(reduction='sum')
model
Sequential(
(0): Linear(in_features=2, out_features=3, bias=True)
(1): Sigmoid()
(2): Linear(in_features=3, out_features=2, bias=True)
)
Como optimizador utilizaremos el Adam
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2)
Primero realizamos una predicción (inferencia) con:
hatY = model(X)
hatY
tensor([[-0.5435, -0.2738],
[-0.6110, -0.3163],
[-0.4007, -0.0868],
[-0.4353, -0.0844]], grad_fn=<AddmmBackward0>)
Luego calculamos la función de pérdida:
loss = criterion(hatY, Y)
loss
tensor(3.0837, grad_fn=<NllLossBackward0>)
En seguida calculamos el gradiente de la función de pérdida:
loss.backward()
Los gradientes se guardan en el atributo grad de todos los pesos y sesgos (parámetros) de la red:
model[0].weight.grad, model[0].bias.grad
(tensor([[-0.0361, -0.0448],
[ 0.0359, 0.0351],
[ 0.0051, 0.0038]]),
tensor([ 0.0542, -0.0474, -0.0047]))
model[2].weight.grad, model[2].bias.grad
(tensor([[-0.2650, -0.6544, -0.5589],
[ 0.2650, 0.6544, 0.5589]]),
tensor([-1.3048, 1.3048]))
Finalmente actualizamos los parámetros usando la función step de nuestro optimizador
Los parámetros actuales de la primera capa son:
model[0].weight, model[0].bias
(Parameter containing:
tensor([[ 0.6084, 0.3615],
[ 0.1907, -0.0184],
[-0.5428, 0.5596]], requires_grad=True),
Parameter containing:
tensor([-0.5945, 0.1355, -0.3496], requires_grad=True))
optimizer.step()
Los parámetros luego de hacer la actualización son:
model[0].weight, model[0].bias
(Parameter containing:
tensor([[ 0.6184, 0.3715],
[ 0.1807, -0.0284],
[-0.5528, 0.5496]], requires_grad=True),
Parameter containing:
tensor([-0.6045, 0.1455, -0.3396], requires_grad=True))
Truco
Para interpretar la salida de la red como probabilidades podemos aplicar una activación nn.Softmax(dim=1) como se muestra a continuación.
nn.Softmax(dim=1)(hatY).detach()
tensor([[0.4330, 0.5670],
[0.4269, 0.5731],
[0.4222, 0.5778],
[0.4132, 0.5868]])
Cada columna representa a una clase y cada fila a un ejemplo. Los valores están siempre entre cero y uno, y además las filas suman uno
Más en general el proceso de ajuste se realiza iterativamente durante un cierto número de pasos o “épocas” de entrenamiento como se muestra a continuación:
for nepoch in range(1000):
hatY = model.forward(X)
optimizer.zero_grad()
loss = criterion(hatY, Y)
loss.backward()
optimizer.step()
if nepoch % 100 == 0:
print(f"{nepoch} {loss.item():0.2f} {torch.nn.Softmax(dim=1)(hatY)[:, 1].detach()}")
0 3.03 tensor([0.5562, 0.5608, 0.5669, 0.5745])
100 0.79 tensor([0.0398, 0.1102, 0.1771, 0.6459])
200 0.19 tensor([0.0078, 0.0315, 0.0410, 0.9014])
300 0.08 tensor([0.0037, 0.0145, 0.0179, 0.9549])
400 0.05 tensor([0.0022, 0.0086, 0.0103, 0.9733])
500 0.03 tensor([0.0015, 0.0057, 0.0069, 0.9820])
600 0.02 tensor([0.0011, 0.0041, 0.0049, 0.9869])
700 0.02 tensor([8.9189e-04, 3.1499e-03, 3.7359e-03, 9.8999e-01])
800 0.01 tensor([7.1810e-04, 2.4861e-03, 2.9403e-03, 9.9207e-01])
900 0.01 tensor([5.9280e-04, 2.0164e-03, 2.3796e-03, 9.9354e-01])
Nota
Paso a paso, el error (función de costo) disminuye y la predicción del modelo se acerca a la etiqueta
Y
tensor([0, 0, 0, 1])
13.3. Entrenamiento por minibatches#
Si el dataset del problema es de gran tamaño no es conveniente utilizar el conjunto completo para calcular la función de costo y derivar.
En general actualizamos el modelo presentandole subconjuntos (minibatches) del dataset
Nota
Esto es lo que se conoce como la estimación estocástica del gradiente descedente (SGD)
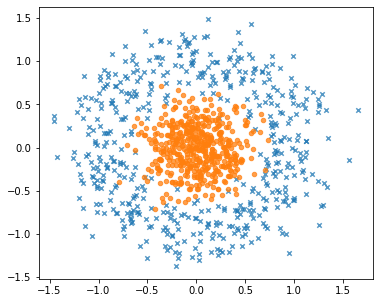
A continuación veremos algunas clases de PyTorch que facilitan la interacción entre el modelo y el conjunto de entrenamiento. A modo de ejemplo crearemos un conjunto de datos sintético con dos atributos, dos clases y que no es linealmente separable:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets
np.random.seed(0)
X, y = sklearn.datasets.make_circles(n_samples=1000, noise=0.2, factor=0.25)
fig, ax = plt.subplots(figsize=(6, 5))
for k, marker in enumerate(['x', 'o']):
mask = y == k
ax.scatter(X[mask, 0], X[mask, 1], s=20, marker=marker, alpha=0.75)
El súbmodulo torch.utils.data tiene los objetos que facilitan la interacción con datos
Sus clases principales son
Dataset: Clase abstracta que representa a un conjunto de datosSubset: Clase que representa una partición de un conjunto de datos, por ejemplo la partición de entrenamiento o validaciónDataLoader: Generador que recibe un conjunto de datos y retorna subconjuntos (minibatches) iterativamente
El primer paso es crear una clase que represente nuestro conjunto de datos en particular, esta clase debe heredar de Dataset y debe implementar las funciones __len__ y __getitem__
import torch.utils.data as data
class CircleDataset(data.Dataset):
def __init__(self, data: np.ndarray, labels: np.ndarray):
self.data = torch.from_numpy(data.astype('float32'))
self.labels = torch.from_numpy(labels.astype('int'))
def __getitem__(self, idx: int):
return (self.data[idx], self.labels[idx])
def __len__(self):
return len(self.labels)
dataset = CircleDataset(X, y)
dataset[0], len(dataset)
((tensor([0.3359, 0.0898]), tensor(1)), 1000)
donde
El constructor recibe los datos y los convierte en formato tensor
__getitem__, recibe un índice y retorna una tupla (dato, etiqueta)__len__retorna la cantidad de ejemplos del conjunto de datos
Para crear particiones de este dataset podemos utilizar la función random_split del módulo data. Esta función recibe el dataset, los tamaños de cada partición y una semilla aleatoria
train_set, valid_set, test_set = data.random_split(dataset, [600, 200, 200],
generator=torch.Generator().manual_seed(1234))
Finalmente creamos objetos DataLoader para obtener minibatches de entrenamiento, validación y prueba con:
train_loader = data.DataLoader(train_set, shuffle=True, batch_size=32)
valid_loader = data.DataLoader(valid_set, shuffle=False, batch_size=128)
test_loader = data.DataLoader(test_set, shuffle=False, batch_size=128)
Los argumentos principales de esta clase son:
Un objeto
DatasetoSubsetshuffle: Booleano que índica si los ejemplos se muestran de forma ordenada o desordenadabatch_size: Entero que indica la cantidad de ejemplos por minibatch
Importante
Es conveniente presentar el conjunto de entrenamiento en distinto orden en cada época. Utiliza shuffle=True para este conjunto.
Una vez creado el objeto DataLoader se puede ocupar de forma equivalente a otros iteradores de Python:
for batchx, batchy in train_loader:
break
batchx.T, batchy
(tensor([[ 5.8060e-03, 3.9618e-01, -2.1615e-01, -1.4567e+00, 8.9777e-02,
-8.4204e-01, -1.3546e-02, -5.3465e-01, 1.1073e-01, 8.1661e-01,
1.1322e-01, 8.5403e-01, -1.7986e-01, -7.6658e-01, 7.8203e-01,
-6.7067e-01, -2.4749e-01, 7.7392e-01, -2.6569e-01, -1.0139e+00,
1.6972e-01, -4.8297e-01, -4.6460e-01, 1.2651e-03, -3.6006e-01,
4.0705e-01, -6.5095e-01, -5.1035e-02, -1.6224e-01, 1.2680e+00,
1.1209e+00, 5.4708e-01],
[ 2.7475e-02, -2.7057e-01, 4.6566e-01, 3.0285e-01, 1.4572e-01,
6.5266e-02, -1.1583e+00, -3.4511e-01, 4.3440e-01, -5.9045e-01,
3.1949e-01, 4.0839e-01, -6.9010e-02, 3.3542e-01, -2.9861e-01,
5.9069e-01, -1.9815e-01, -5.1124e-01, -3.1567e-01, 3.3081e-01,
-3.0929e-01, 4.3608e-01, -3.5730e-01, -1.9970e-01, 1.2396e+00,
-8.5842e-02, -5.7960e-01, 2.3860e-01, -7.7749e-01, -6.7565e-01,
5.6453e-01, 3.7583e-01]]),
tensor([1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1,
0, 1, 0, 1, 0, 0, 0, 0]))
13.4. Esquema general de entrenamiento en PyTorch#
Habiendo definido el modelo, el criterio, el optimizador y los datos, el esquema general de entrenamiento de un modelo en PyTorch sería:
for epoch in range(num_epochs): # Durante un cierto número de épocas
for minibatch in data: # Para cada minibatch de datos
optimizer.zero_grad() # Limpiamos los gradientes
x, y = minibatch # Desempaquetamos
yhat = model.forward(x) # Predecimos
loss = criterion(yhat, y) # Evaluamos
loss.backward() # Calculamos los gradientes
optimizer.step() # Actualizamos los parámetros
donde
Una época es una presentación completa del conjunto de entrenamiento
Un minibatch es un subconjunto del conjunto de entrenamiento
Adicionalmente, debemos considerar un bucle de validación donde sólo realizamos predicción y evaluación de la loss con el objetivo de detectar sobre-ajuste
- Early Stopping
Detención del entrenamiento cuando la loss de validación no haya disminuido durante una cierta cantidad de épocas (paciencia). Se utiliza para evitar el sobreajuste
Importante
En cada época, verifica que si el error de validación representa un nuevo mínimo. Si es así puedes respaldar el modelo utilizado torch.save
A continuaciones se ponen en práctica estos criterios utilizando PyTorch. Por conveniencia se implementan las siguientes funciones
update_step: Recibe un minibatch y actualiza los parámetrosevaluation_step: Recibe un minibtach y evalúa el criterio de optimizacióntrain_one_epoch: Realiza una época de entrenamiento. Se encarga de guardar el modelo si es el mejor encontrado hasta ese punto
def update_step(data, label):
prediction = model(data)
optimizer.zero_grad()
loss = criterion(prediction, label)
loss.backward()
optimizer.step()
return loss.item()
def evaluate_step(data, label):
prediction = model(data)
loss = criterion(prediction, label)
return loss.item()
def train_one_epoch(epoch):
train_loss, valid_loss = 0.0, 0.0
for batchx, batchy in train_loader:
train_loss += update_step(batchx, batchy)
for batchx, batchy in valid_loader:
valid_loss += evaluate_step(batchx, batchy)
# Guardar modelo si es el mejor hasta ahora
global best_valid_loss
if epoch % 10 == 0:
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save({'epoca': epoch,
'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'loss': valid_loss},
'best_model.pt')
return train_loss/len(train_loader.dataset), valid_loss/len(valid_loader.dataset)
Nota
Para entrenar en GPU sería necesario
que el modelo esté en memoría de GPU
enviar los datos y etiquetas a GPU antes de realizar los cálculos.
En este caso el modelo se entrena por 500 épocas
%%time
def circle_model(n_hidden: int):
return nn.Sequential(nn.Linear(2, n_hidden), nn.Sigmoid(), nn.Linear(n_hidden, 2))
model = circle_model(10)
criterion = torch.nn.CrossEntropyLoss(reduction='sum')
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2)
max_epochs, best_valid_loss = 500, np.inf
running_loss = np.zeros(shape=(max_epochs, 2))
for epoch in range(max_epochs):
running_loss[epoch] = train_one_epoch(epoch)
fig, ax = plt.subplots(figsize=(7, 4), tight_layout=True)
ax.plot(running_loss[:, 0], label='Entrenamiento')
ax.plot(running_loss[:, 1], label='Validación')
ax.set_xlabel('Epoch')
ax.set_ylabel('Loss')
ax.legend();
CPU times: user 2min 6s, sys: 86.8 ms, total: 2min 6s
Wall time: 32.1 s
<matplotlib.legend.Legend at 0x7fbef9e85eb0>
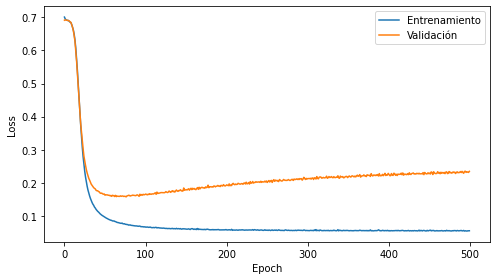
Cargamos la información serializada del modelo utilizado torch.load
saved_model = torch.load('best_model.pt')
El mejor modelo se obtuvo en la época
saved_model['epoca']
70
Podemos asignar los mejores parámetros al modelo anterior con:
model = circle_model(10)
model.load_state_dict(saved_model['model_state_dict'])
<All keys matched successfully>
Podemos evaluar el mejor modelo en el conjunto de test para analizar su capacidad de generalización
from sklearn.metrics import classification_report
ytrue, ypred = [], []
for x, y_ in test_loader:
ypred.append(nn.Softmax(dim=1)(model(x)).detach().argmax(dim=1))
ytrue.append(y_)
ytrue, ypred = np.concatenate(ytrue), np.concatenate(ypred)
print(classification_report(ytrue, ypred))
precision recall f1-score support
0 0.97 0.98 0.98 104
1 0.98 0.97 0.97 96
accuracy 0.97 200
macro avg 0.98 0.97 0.97 200
weighted avg 0.98 0.97 0.97 200
En este caso también podemos visualizar el resultado de predicción en el espacio de características:
x_test = np.arange(-2, 2, 0.05, dtype=np.float32)
x_test1, x_test2 = np.meshgrid(x_test, x_test)
x_test = torch.from_numpy(np.stack((x_test1.ravel(), x_test2.ravel())).T)
prob_test = nn.Softmax(dim=1)(model(x_test)).detach()[:, 1].reshape(x_test1.shape)
fig, ax = plt.subplots(figsize=(6, 5))
ax.pcolormesh(x_test1, x_test2, prob_test, cmap=plt.cm.RdBu_r)
for k, marker in enumerate(['x', 'o']):
mask = y == k
ax.scatter(X[mask, 0], X[mask, 1], c='k', s=20, marker=marker, alpha=0.5)
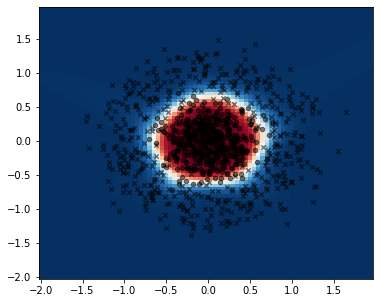
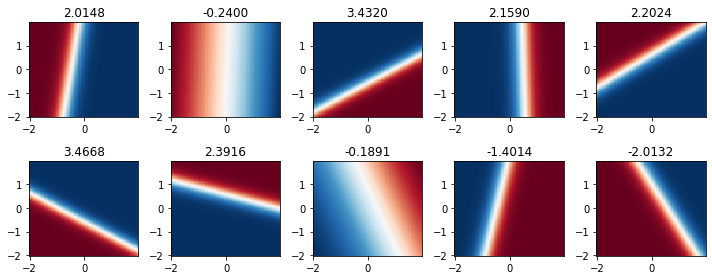
El resultado en la capa de salida tiene forma circular. Sin embargo, si inspeccionemos la salida de la capa oculta, que en este caso tiene 10 neuronas:
fig, ax = plt.subplots(2, 5, figsize=(10, 4), tight_layout=True)
for ax_, layer, w in zip(ax.ravel(), model[0](x_test).T, model[2].weight.detach()[0]):
ax_.pcolormesh(x_test1, x_test2,
nn.Sigmoid()(layer).reshape(x_test1.shape).detach(),
cmap=plt.cm.RdBu_r)
ax_.set_title(f"{w.item():0.4f}")
Nota
La capa de salida combina los hiperplanos de la capa oculta para formar un circulo. Sobre cada neurona oculta se muestra su peso en la capa de salida. Mientras más cercano a cero, menos relevante es su aporte.
13.5. Diagnósticos a partir de curvas de aprendizaje#
Podemos diagnosticar el entrenamiento observando la evolución de la función de costo
Importante
Siempre visualiza la loss en ambos conjuntos: entrenamiento y validación
Veamos algunos casos
Ambas curvas en descenso
Si las curvas se ven así:
epochs = np.arange(1, 500)
loss_train = (epochs)**(-1/10) + 0.01*np.random.randn(len(epochs))
loss_valid = (epochs)**(-1/10) + 0.01*np.random.randn(len(epochs)) + 0.1
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(epochs, loss_train, lw=2, label='entrenamiento')
ax.plot(epochs, loss_valid, lw=2, label='validación')
ax.set_ylim([0.5, 1.05])
plt.legend();
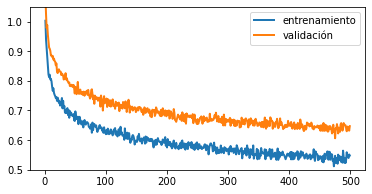
En este caso deberías continuar con el entrenamiento, pues no hay señal de convergencia
Sobreajuste temprano
Si las curvas se ven así:
epochs = np.arange(1, 500)
loss_train = (epochs)**(-1/10) + 0.01*np.random.randn(len(epochs))
loss_valid = (epochs)**(-1/10) + 0.00001*(epochs)**2 +0.01*np.random.randn(len(epochs)) + 0.01
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(epochs, loss_train, lw=2, label='entrenamiento')
ax.plot(epochs, loss_valid, lw=2, label='validación')
ax.set_ylim([0.5, 1.05])
plt.legend();
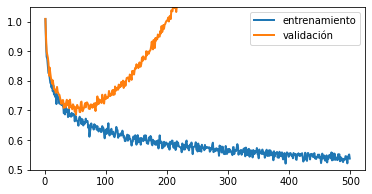
Significa que tu modelo se ha sobreajustado, por ende:
Implementa un modelo más sencillo
Consigue más datos
Considera utilizar regularización
Error en el código o mal punto de partida
Si tus curvas se ven así:
epochs = np.arange(1, 500)
loss_train = 1.0 + 0.01*np.random.randn(len(epochs))
loss_valid = 1.0 + 0.01*np.random.randn(len(epochs)) + 0.01
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(epochs, loss_train, lw=2, label='entrenamiento')
ax.plot(epochs, loss_valid, lw=2, label='validación')
#ax.set_ylim([0.5, 1.05])
plt.legend();
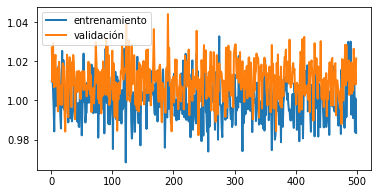
Revisa que tu código no tenga bugs, causas comunes de error:
el modelo no esté recibiendo adecuadamente los datos y/o la etiqueta
los datos tiene un rango muy grande y los gradientes explotan: normaliza los datos
la función de costo no es la adecuada para el problema
la taza de aprendizaje es demasiado alta
También puede deberse a una muy mala inicialización aleatoria, reinicia el entrenamiento para comprobar si es el caso