14. Procesamiento digital de imágenes

Una imagen es una colección de pixeles ordenados. En estándar RGB cada pixel corresponde a 3 valores enteros de 8 bit (256 niveles). Combinándolos formamos colores (aproximadamente 16.7M)

Otra codificación usual para los pixeles consiste en usar un número entre cero y uno para cada canal (color). El estándar RGBA añade un canal que representa la opacidad. Las imágenes en escala de grises y sin opacidad se pueden representar usando un canal

A continuación se muestra una imagen transformada a escala de grises mediante una combinación de sus canales de color:

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

img = plt.imread('img/cameraman.png')

def to_grayscale(img):
    return np.dot(img[:, :, :3], 
                  np.array([0.2989, 0.587, 0.114]))

img_bw = to_grayscale(img)

display(img_bw.shape)
display(img_bw.dtype)

plt.figure(figsize=(4, 4), tight_layout=True)
plt.imshow(img_bw, cmap=plt.cm.Greys_r);

(327, 326)

dtype('float64')

Para nuestros sistemas digitales una imagen es una arreglo multidimensional y podemos operarlo como tal

¿A qué corresponde este segmento del arreglo?

subimg = np.copy(img_bw[50:100, 120:180])
display(subimg)

array([[0.72541766, 0.72933884, 0.72933884, ..., 0.72149649, 0.71757531,
        0.71365413],
       [0.72541766, 0.73326002, 0.73326002, ..., 0.71757531, 0.71365413,
        0.71365413],
       [0.73718119, 0.72541766, 0.72541766, ..., 0.71757531, 0.70189061,
        0.72541766],
       ...,
       [0.03529059, 0.03136941, 0.03136941, ..., 0.15684706, 0.14116236,
        0.18821647],
       [0.03529059, 0.02744824, 0.02744824, ..., 0.15684706, 0.14116236,
        0.23527059],
       [0.03529059, 0.03136941, 0.02352706, ..., 0.15292589, 0.13332001,
        0.27448237]])

plt.figure(figsize=(3, 3), tight_layout=True)
plt.imshow(subimg, cmap=plt.cm.Greys_r);

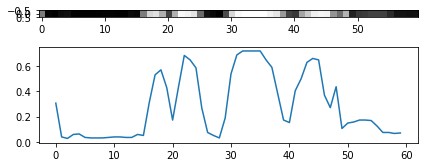
¿Y este segmento?

fig, ax = plt.subplots(2, 1, figsize=(6, 3), tight_layout=True)
ax[1].plot(subimg[30, :])
ax[0].imshow(subimg[30:31, :], cmap=plt.cm.Greys_r);

14.1. Convolución y correlación cruzada discreta

Una herramienta clásica de procesamiento digital de señales es la convolución

La operación de convolución entre dos señales unidimensionales discretas es

\[ (f * g) [n] = \sum_{m=-\infty}^\infty f[m] g[n-m] \]

y la operación de correlación cruzada es

\[ (f \star g) [n] = \sum_{m=-\infty}^\infty f[m] g[m+n] \]

Nota

Para ambas operaciones el resultado es una nueva señal que también depende de \(n\)

Por ejemplo el elemento \(0\) de \(f\star g\) se calcula como

f[0] g[0] + f[1] g[1] + f[2] g[2] + ...

Luego el elemento \(1\) sería

f[0] g[1] + f[1] g[2] + f[2] g[3] + ...

14.2. Filtrado de imágenes con convoluciones

Se puede extender el concepto de convolución a dos dimensiones

\[ (I_1 * I_2) [n_1, n_2] = \sum_{m_1=-\infty}^\infty \sum_{m_2=-\infty}^\infty I_1[m_1, m_2] I_2[n_1-m_2, n_2 - m_2] \]

donde \(n_1\) es el índice de las filas y \(n_2\) es el índice de las columnas

Nota

La convolución entre dos imágenes es una nueva imagen

• La imagen \(I_1\) es la entrada

• La imagen \(I_2\) se denomina filtro o kernel de la convolución

• La imagen resultante es la imagen filtrada

Filtro pasa-bajo

Suaviza, elimina los detalles

import scipy.signal

D = 3
filt = np.ones(shape=(D, D))

display(filt)
img_res = scipy.signal.correlate2d(subimg, filt/np.sum(filt), mode='valid')

fig, ax = plt.subplots(1, 3, figsize=(8, 3), tight_layout=True)
ax[0].imshow(subimg, cmap=plt.cm.Greys_r)
ax[1].imshow(filt, cmap=plt.cm.Greys_r)
ax[2].imshow(img_res, cmap=plt.cm.Greys_r);

array([[1., 1., 1.],
       [1., 1., 1.],
       [1., 1., 1.]])

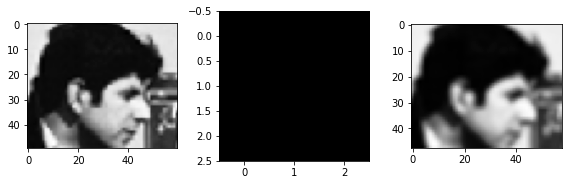
Filtro pasa-alto

Resalta los cambios bruscos, elimina las partes “planas”

filt = np.array([[1., -1.]]*2)
display(filt)
img_res = scipy.signal.correlate2d(subimg, filt, mode='valid')

fig, ax = plt.subplots(1, 3, figsize=(8, 3), tight_layout=True)
ax[0].imshow(subimg, cmap=plt.cm.Greys_r)
ax[1].imshow(filt, cmap=plt.cm.Greys_r)
ax[2].imshow(img_res, cmap=plt.cm.Greys_r);

array([[ 1., -1.],
       [ 1., -1.]])

¿Detector de patillas?

Detecta patillas de fotografos mirando al horizonte

filt = np.ones(shape=(11, 11))
filt[:9, 2:9] = 0
display(filt)

array([[1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
       [1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
       [1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
       [1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
       [1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
       [1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
       [1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
       [1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
       [1., 1., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
       [1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])

img_res = scipy.signal.correlate2d(subimg, filt-np.mean(filt), mode='valid')

fig, ax = plt.subplots(1, 3, figsize=(8, 3), tight_layout=True)
ax[0].imshow(subimg, cmap=plt.cm.Greys_r)
maxloc = np.unravel_index(np.argmax(img_res), shape=img_res.shape)
ax[0].scatter(maxloc[1]+filt.shape[0]//2, maxloc[0]+filt.shape[1]//2, c='r', s=20)
ax[1].imshow(filt, cmap=plt.cm.Greys_r)
ax[2].imshow(img_res, cmap=plt.cm.Reds);

En realidad el filtro se activa con cualquier cosa con forma de “U”

Importante

Podríamos aprender filtros para detectar objetos específicos

En tal caso necesitamos aprender los valores de los “píxeles” del kernel