12. Breve tutorial de PyTorch

PyTorch es una librería de alto nivel para Python que provee

1. Una clase tensor para hacer cómputo de alto rendimiento con capacidad de auto-diferenciación

2. Un plataforma para crear y entrenar redes neuronales

En tutorial revisaremos en detalle como se crean y manipulan tensores. Luego veremos como el submódulo torch.nn para crear redes neuronales artificiales

Instalación

Lo más recomendable para instalar esta librería es crear un ambiente de desarrollo con conda y ejecutar

conda install pytorch torchvision cudatoolkit=11.3 ignite -c pytorch

en caso de tener GPU o con

conda install pytorch torchvision cpuonly ignite -c pytorch

sino se cuenta con GPU

Ver también

Si no haz utilizado conda recomiendo revisar aquí

import torch
torch.__version__

'1.11.0'

12.1. Objeto Tensor

La clase torch.Tensor es muy similar en uso al ndarray de NumPy. Un tensor corresponde a una matriz o arreglo n-dimensional con tipo definido que soporta operaciónes vectoriales de tipo SIMD y broadcasting

A continuación revisaremos las operaciones más fundamentales relacionadas a tensores

Creación de tensores

Un tensor puede crearse usando

• constructores de torch

• a partir de listas de Python o ndarray de NumPy

Por ejemplo para crear un vector de largo 10 relleno de ceros:

torch.zeros(10)

tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

Un vector de largo 10 relleno de unos:

torch.ones(10)

tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

Un vector con 10 números partiendo en cero y terminando en nueve

torch.linspace(0, 9, steps=10)

tensor([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

Un tensor construido a partir de una lista:

una_lista = [0, 1, 2, 3, 4, 5, 6]
torch.Tensor(una_lista)

tensor([0., 1., 2., 3., 4., 5., 6.])

Un tensor construido a partir de un ndarray

import numpy as np
numpy_array = np.random.randn(10)
torch.from_numpy(numpy_array)

tensor([ 2.3634,  0.7277,  1.7162, -0.4610,  0.7706, -0.7328,  0.5429, -0.3567,
         0.4777, -1.4907], dtype=torch.float64)

De PyTorch a NumPy

Para convertir un tensor de pytorch a un ndarray de numpy se utiliza el método numpy():

data = torch.randn(5)
data

tensor([ 0.9727, -0.7704, -0.9177,  2.9054, -0.0273])

data.numpy()

array([ 0.97273713, -0.770423  , -0.9177197 ,  2.905431  , -0.02733249],
      dtype=float32)

Atributos importantes de los tensores

Un tensor tiene un tamaño (dimesiones) y tipo específico. Esto se consulta con los atributos ndim/shape y dtype

a = torch.randn(10, 20, 30)
a.ndim, a.shape, a.dtype

(3, torch.Size([10, 20, 30]), torch.float32)

Un tensor puede estar alojado en la memoria del sistema (‘cpu’) o en la memoria de dispositivo (‘gpu’), esto se consulta con el atributo device:

a.device

device(type='cpu')

Cuando se crea un tensor se puede especificar el tipo y el dispositivo

a = torch.zeros(10, dtype=torch.int32, device='cpu')
display(a)

tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0], dtype=torch.int32)

Manipulación de tensores

Sea el siguiente tensor de una dimensión:

a = torch.linspace(0, 9, 10)
a

tensor([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

Podemos reorganizar las dimensiones del tensor con el método reshape:

b = a.reshape(2, 5)
b

tensor([[0., 1., 2., 3., 4.],
        [5., 6., 7., 8., 9.]])

Podemos transponer el método transpose() o su alias T

b.T

tensor([[0., 5.],
        [1., 6.],
        [2., 7.],
        [3., 8.],
        [4., 9.]])

Podemos convertir un tensor de dimensión arbitraria a uno de una dimensión con flatten()

b.flatten()

tensor([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])

Podemos agregar una dimensión en una posición arbitraria con unsqueeze(d)

c = b.unsqueeze(1)
c, c.shape

(tensor([[[0., 1., 2., 3., 4.]],
 
         [[5., 6., 7., 8., 9.]]]),
 torch.Size([2, 1, 5]))

Cálculos con tensores

Un tensor soporta operaciones aritméticas y lógicas

Nota

Si el tensor está en memoria de sistema entonces las operaciones son realizadas por la CPU

data = torch.linspace(0, 5, steps=6)
data

tensor([0., 1., 2., 3., 4., 5.])

Algunos ejemplos de operaciones aritméticas

data + 5

tensor([ 5.,  6.,  7.,  8.,  9., 10.])

2*data

tensor([ 0.,  2.,  4.,  6.,  8., 10.])

data.pow(2)

tensor([ 0.,  1.,  4.,  9., 16., 25.])

data.log()

tensor([  -inf, 0.0000, 0.6931, 1.0986, 1.3863, 1.6094])

Una operación lógica puede utilizarse para filtrar un tensor:

mask = data > 3
mask

tensor([False, False, False, False,  True,  True])

data[mask]

tensor([4., 5.])

Un ejemplo de broadcasting:

data2 = torch.ones(6)
data.unsqueeze(1), data2.unsqueeze(0), data.unsqueeze(1)*data2.unsqueeze(0)

(tensor([[0.],
         [1.],
         [2.],
         [3.],
         [4.],
         [5.]]),
 tensor([[1., 1., 1., 1., 1., 1.]]),
 tensor([[0., 0., 0., 0., 0., 0.],
         [1., 1., 1., 1., 1., 1.],
         [2., 2., 2., 2., 2., 2.],
         [3., 3., 3., 3., 3., 3.],
         [4., 4., 4., 4., 4., 4.],
         [5., 5., 5., 5., 5., 5.]]))

Cálculos en GPU

Usando el atributo to podemos intercambiar un tensor entre memoría de GPU (‘device’) y CPU (‘host’)

data = torch.zeros(10)
data = data.to('cuda')

Importante

Cuando todos los tensores involucrados en una operaciones están en memoria de dispositivo entonces el cálculo lo hace la GPU

La siguiente nota indica las opciones para intercambiar datos entre GPU y CPU que ofrece PyTorch: https://pytorch.org/docs/stable/notes/cuda.html

Nota

Una Graphical Processing Unit (GPU) o tarjeta de video es un hardware para hacer cálculos sobre mallas tridimensionales, generación de imágenes (rendering) y otras tareas gráficas. A diferencia de la CPU, la GPU es especialista en cálculo paralelo y tiene miles de nucleos (NVIDIA RTX 2080: 2944 nucleos)

12.2. Auto-diferenciación con Tensores

En general, las redes neuronales se entrenan usando Gradiente descedente. Por lo tanto necesitamos calcular las derivadas de la función de costo para todos los parámetros de la red

PyTorch tiene incorporado un sistema de diferenciación automática denominado autograd

Para poder derivar una función en pytorch

1. Se necesita que su entrada sean tensores con el atributo requires_grad=True

2. Luego llamamos la función backward() de la función

3. El resultado queda guardado en el atributo grad de la entrada (nodo hoja)

Ejemplo

%matplotlib inline 
import matplotlib.pyplot as plt

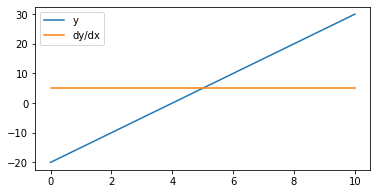
x = torch.linspace(0, 10, steps=1000, requires_grad=True)
y = 5*x - 20
y.backward(torch.ones_like(x))

fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(x.detach().numpy(), y.detach().numpy(), label='y')
ax.plot(x.detach().numpy(), x.grad.detach().numpy(), label='dy/dx')
plt.legend();

x = torch.linspace(0, 10, steps=1000, requires_grad=True)
y = torch.sin(2.0*np.pi*x)*torch.exp(-(x-5).pow(2)/3)
y.backward(torch.ones_like(x))

fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(x.detach().numpy(), y.detach().numpy(), label='y')
ax.plot(x.detach().numpy(), x.grad.detach().numpy(), label='dy/dx')
plt.legend();

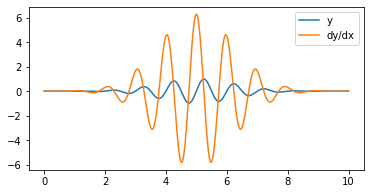
Comparado con la derivada calculada “a mano”:

dydx = 2*torch.pi*torch.cos(2.0*np.pi*x)*torch.exp(-(x-5).pow(2)/3) - 2/3*(x-5)*torch.sin(2.0*np.pi*x)*torch.exp(-(x-5).pow(2)/3)
torch.sum(torch.pow(x.grad.detach() - dydx, 2))

tensor(1.1211e-11, grad_fn=<SumBackward0>)

12.3. Grafo de cómputo

Cuando concatenamos operacionesm PyTorch construye internamente un “grafo de cómputo”

\[ x \to z = f_1(x) \to y = f_2(z) \]

El método backward() calcula los gradientes y los almacena en los nodo hoja que tengan requires_grad=True

Por ejemplo

y.backward : Guarda dy/dx en x.grad

z.backward : Guarda dz/dx en x.grad

Nota

backward() implementa la regla de la cadena de las derivadas

backward recibe una entrada: La derivada de la etapa superior de la cadena. Por defecto usa torch.ones([1]), es decir que asume que está en el nivel superior del grafo y que la salida es escalar (unidimensional)

x = torch.linspace(0, 10, steps=1000, requires_grad=True) # Nodo hoja
x.grad_fn

z = torch.sin(2*x)
z.grad_fn

<SinBackward0 at 0x7fa4111072b0>

y = z.pow(2)/2
y.grad_fn

<DivBackward0 at 0x7fa4111073d0>

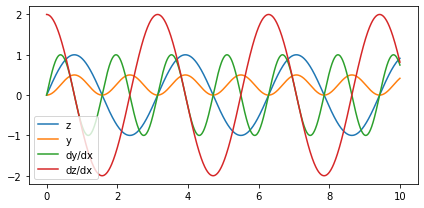
fig, ax = plt.subplots(figsize=(6, 3), tight_layout=True)
ax.plot(x.detach().numpy(), z.detach().numpy(), label='z')
ax.plot(x.detach().numpy(), y.detach().numpy(), label='y')
# Derivada dy/dx
y.backward(torch.ones_like(x), retain_graph=True)
ax.plot(x.detach().numpy(), x.grad.detach().numpy(), label='dy/dx')
# Borro el resultado en x.grad
x.grad = None
# Derivada dz/dx
z.backward(torch.ones_like(x))
ax.plot(x.detach().numpy(), x.grad.detach().numpy(), label='dz/dx')
plt.legend();

Nota

El método detach() retorna una copia del tensor que se ha “despegado” del grafo

12.4. Construcción de redes neuronales

PyTorch nos ofrece la clase tensor y las funcionalidades de autograd. Estas poderosas herramientas nos dan todo lo necesario para construir y entrenar redes neuronales artificiales

Para facilitar aun más estas tareas PyTorch tiene módulos de alto nivel que implementan

1. Modelo base de red neuronal: torch.nn.Module

2. Distintos tipos de capas, funciones de activación y funciones de costo: torch.nn

3. Distintos algoritmos de optimización basados en gradiente descedente: torch.optim

Una red neuronal en PyTorch es una clase de Python que hereda de torch.nn.Module. Como mínimo esta clase debe implementar las funciones __init__ y forward

• El constructor define las capas que se utilizaran

• Heredar de nn.Module hace que los parámetros de las capas queden registrados por la máquina de estado de PyTorch

• La función forward recibe como argumento los datos de entrada y retorna la predicción del modelo, es decir que define como se conectan las capas

Nota

La función forward() actua como la función __call__() de Python, es decir que se creamos una objeto model que herada de nn.Module llamar model.forward(x) es equivalente a model(x)

12.4.1. Capa completamente conectada

Una capa completamente conectada (fully-connected) también llamada capa densa, implementa la siguiente operación

\[ z = wx + b \]

donde \(x\) son los datos que entran en la capa y \(w/b\) son los parámetros de la capa (pesos y sesgos) de la capa

Esta capa está implementada en Pytorch como torch.nn.Linear. El constructor de este objeto espera la dimensionalidad (número de neuronas) de entrada y salida de la capa

Por ejemplo para crear una capa como el siguiente diagrama

usariamos

dense = torch.nn.Linear(3, 2)

Una vez creada la podemos evaluar con dense(data) o dense.forward(data)

Nota

Las capas son a su vez instancias de torch.nn.Module. Es decir que un módulo puede tener otros módulos anidados

12.4.2. Funciones de activación

Las funciones de activación más comunes de la literatura están implementadas como clases en torch.nn

Veamos algunos ejemplos para aprender a utilizarlas:

data = torch.linspace(-5, 5, steps=100)

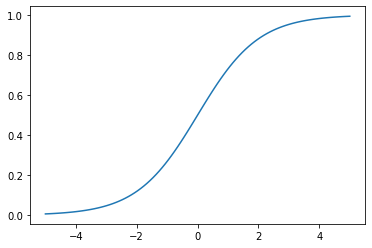
activation = torch.nn.Sigmoid()

fig, ax = plt.subplots()
ax.plot(data.detach(), activation(data).detach());

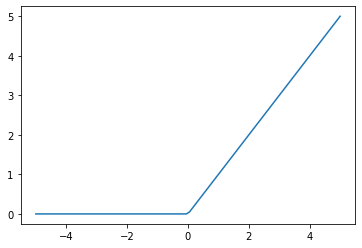
activation = torch.nn.ReLU()

fig, ax = plt.subplots()
ax.plot(data.detach(), activation(data).detach());

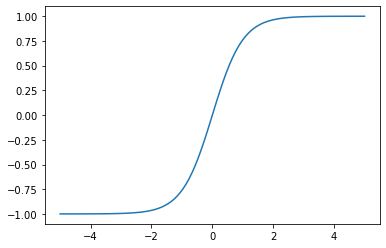
activation = torch.nn.Tanh()

fig, ax = plt.subplots()
ax.plot(data.detach(), activation(data).detach());

12.4.3. Perceptron multicapa en Pytorch

Utilicemos lo aprendio para implementar un perceptrón multicapa con una capa oculta y función de activación sigmoide:

import torch
import torch.nn as nn

class MultiLayerPerceptron(nn.Module):

    def __init__(self, input_dim, hidden_dim, output_dim): 
        super(type(self), self).__init__()  
        self.hidden = nn.Linear(input_dim, hidden_dim)
        self.output = nn.Linear(hidden_dim, output_dim)        
        self.activation = nn.Sigmoid()
        
    def forward(self, x):
        x = self.activation(self.hidden(x))
        return self.output(x)

Crear una capa Linear hace que se registren sus parámetros weight y bias en el grafo. Inicialmente los parámetros tienen valores aleatorios

model = MultiLayerPerceptron(input_dim=2, output_dim=1, hidden_dim=2)
model.hidden.weight, model.hidden.bias

(Parameter containing:
 tensor([[0.6125, 0.4714],
         [0.0419, 0.5960]], requires_grad=True),
 Parameter containing:
 tensor([-0.2803,  0.3135], requires_grad=True))

model.output.weight, model.output.bias

(Parameter containing:
 tensor([[-0.1091, -0.2248]], requires_grad=True),
 Parameter containing:
 tensor([-0.2507], requires_grad=True))

El modelo se evalua sobre un tensor de datos llamando a su función forward

X = 10*torch.rand(10000, 2) - 5
Y = model(X)

PyTorch también admite una forma “más funcional” de crear modelos utilizando torch.nn.Sequential

El modelo anterior sería:

model = nn.Sequential(nn.Linear(2, 2),
                      nn.Sigmoid(),
                      nn.Linear(2, 1))

Esta forma de crear modelos es más consisa pero menos reutilizable