Contents

Stochastic Variational Inference with NumPyro

Stochastic Variational Inference with NumPyro

Previously we learned

  • how to write probabilistic models and perform MCMC with numpyro

  • the fundamental ideas of variational inference (VI)

In this lesson we will explore the tools offered by numpyro to obtain approximate variational posteriors. The unified interface for VI in numpyro is located in numpyro.infer.SVI

The arguments of the SVI object are

numpyro.infer.SVI(model, # A function that defines the generative model 
                  guide, # A function that defines the approximate posterior
                  optim, # A "gradient-descent-based" optimizer
                  loss, # The cost function, a variant of the ELBO
                  static_kwargs # (Optional) Static arguments of model
                 )

See also

SVI corresponds to Stochastic Variational inference, a methodology to scale VI to large databases by subsampling. In SVI, the cost function and its derivatives are estimated as averages over minibatches of data. In summary, SVI is the combination of VI and Stochastic Gradient Descent (SGD)

Through this lesson we consider the following data as example

import holoviews as hv
hv.extension('bokeh')
import jax.numpy as jnp
import jax.random as random
import numpyro.distributions as dists
import numpyro

numpyro.set_platform("cpu") 
numpyro.set_host_device_count(2) 
# print(numpyro.__version__)

key = random.PRNGKey(1234)
w_true, b_true, s_true = 0.5, -0.7, 1.
x = jnp.sort(dists.Normal(0, 5).rsample(key, sample_shape=(10,)))
y = w_true*x + b_true
key, subkey = random.split(key)
y += dists.Normal(0, s_true).rsample(key, sample_shape=(len(y),))

hv.ErrorBars((x, y, s_true)).opts(width=500)

which we will model using a bayesian linear regression

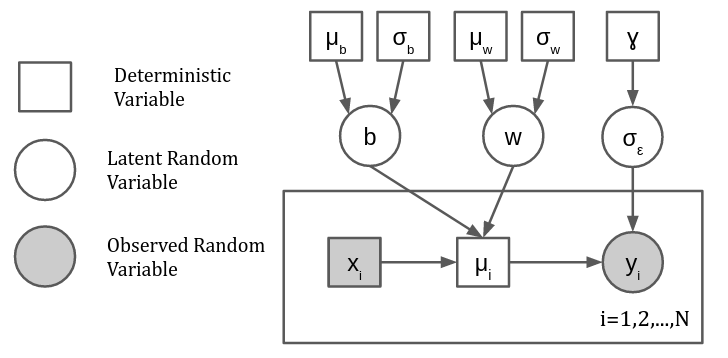
../../_images/linear_regression_plate.png

with hyperparameters \(\mu_b = \mu_\sigma=0\) and \(\sigma_b = \sigma_w = \gamma = 10\)

def model(x, y=None):
    w = numpyro.sample("w", dists.Normal(0.0, 10.0))
    b = numpyro.sample("b", dists.Normal(0.0, 10.0))
    s = numpyro.sample("s_eps", dists.HalfCauchy(10.0))
    with numpyro.plate("data", size=len(x)):
        mu = numpyro.deterministic("mu", x*w+b)
        y = numpyro.sample("y", dists.Normal(mu, s), obs=y)
    return mu

In what follows we review how to set-up the SVI object to obtain a variational posterior for this numpyro model

Guide function

The guide represents \(q_\nu(\theta)\), i.e. it has to specify the approximate posterior distribution of the parameters of the model

In practice, a numpyro guide is a Python function that has to comply with the following:

  • The input arguments have to be the same as those in the model function

  • Every numpyro.sample in the model function needs a numpyro.sample using the same name in the guide

  • The primitive numpyro.param is used to register the hyperparameters of these latent variables

For the bayesian linear regression \(\theta = (w, b, s)\). As an example we will implement a fully factored normal guide following

\[\begin{split} \begin{split} q_\nu(w,b,s) &= q_{\nu_w}(w)q_{\nu_b}(b) q_{\nu_s}(s) \\ &= \mathcal{N}(w|\mu_w, \sigma_w^2) \mathcal{N}(b|\mu_b, \sigma_b^2) \mathcal{N}(\log(s)|\mu_{\log s}, \sigma_{\log s}^2) \end{split} \end{split}\]

The hyperparameters are \(\nu = (\mu_w, \sigma_w, \mu_b, \sigma_b, \mu_{\log s}, \sigma_{\log s})\). We need to register every parameter in \(\nu\) using numpyro.param as these are the values that we will optimize using SVI

from numpyro.distributions import constraints

def guide(x, y=None): 
    # slope
    w_loc = numpyro.param("w_loc", 0.0)
    w_scale = numpyro.param("w_scale", 0.1, constraint=constraints.positive)
    w = numpyro.sample("w", dists.Normal(w_loc, w_scale))
    # intercept
    b_loc = numpyro.param("b_loc", 0.0)
    b_scale = numpyro.param("b_scale", 0.1, constraint=constraints.positive)
    b = numpyro.sample("b", dists.Normal(b_loc, b_scale))
    # noise variance
    s_loc = numpyro.param("s_log_loc", 0.0)
    s_scale = numpyro.param("s_log_scale", 0.1, constraint=constraints.positive)
    s = numpyro.sample("s_eps", dists.TransformedDistribution(dists.Normal(s_loc, s_scale), 
                                                          dists.transforms.ExpTransform()))

Note

We can restrict the value taken by a param using the constraint argument. The constraints submodule offers non-negativity, truncated, circular and simplex constraints, among others

Loss function

In the previous lesson we studied the Evidence Lower Bound (ELBO)

\[\begin{split} \begin{split} \hat \nu &= \text{arg}\max_\nu \mathcal{L}(\nu) \\ &= \text{arg}\max_\nu \int q_\nu(\theta) \log \frac{p(\mathcal{D}|\theta) p (\theta)}{q_\nu(\theta)} d\theta \end{split} \end{split}\]

where

  • The model function defines \(p(\mathcal{D}|\theta) p (\theta)\)

  • The guide function defines \(q_\nu(\theta)\)

Numpyro offers several versions of the ELBO in numpyro.infer, the most common are:

  • Trace_ELBO: Default ELBO. Reduces variance of the gradients using “Rao-Blackwellization”

  • TraceMeanField_ELBO: Assumes Mean-field structure. Reduce variance of gradients using analytical KL when possible

We will study the importance of gradient variance later

Training

The main methods of the SVI object are

  • init: Expects a PRNG key and the model/guide arguments. Initializes the SVI object and returns an SVI state

  • get_params: Expects an SVI state. Returns a dictionary with the model parameters

  • update: Expects an SVI state and the model/guide arguments. Performs a gradient descent step. Returns the update state and the value of the loss

Note

svi.update is similar to the backward() plus step() in pytorch

In this example we select the Adam algorithm as optimizer and the default ELBO as loss function. The example also demostrates how to use jax.jit to improve the computational efficiency of update

Note

Any optax optimizer can be used with SVI

%%time

from jax import jit
import optax
from tqdm.notebook import tqdm

def train_svi(guide, key, lr=0.01, nepochs=1000):
    svi = numpyro.infer.SVI(model, guide, optax.adam(lr), loss=numpyro.infer.Trace_ELBO())
    state = svi.init(key, x, y)
    
    loss_evolution = []
    param_names = list(svi.get_params(state).keys())
    print(param_names)
    param_evolution = {param: [] for param in param_names}
    
    jit_update = jit(svi.update)
    for epoch in tqdm(range(nepochs)):
        state, loss = jit_update(state, x, y)
        loss_evolution.append(loss.item())
        current_params = svi.get_params(state)
        for name, value in current_params.items():
            param_evolution[name].append(value)

    for name, value in current_params.items():
        param_evolution[name] = jnp.stack(param_evolution[name])
    return svi, state, loss_evolution, param_evolution
 
key, key_ = random.split(key)  
svi, state, loss_evolution, param_evolution = train_svi(guide, key_)    

['b_loc', 'b_scale', 's_log_loc', 's_log_scale', 'w_loc', 'w_scale']

CPU times: user 4.59 s, sys: 30 ms, total: 4.62 s
Wall time: 4.62 s

The evolution of the ELBO:

hv.Curve(loss_evolution, 'Epoch', 'Loss').opts(width=500)

And the evolution of the registered parameters:

curves = [hv.Curve(param_evolution[name], 
                   'Epoch', 'Locations', label=name) for name in ['b_loc', 'w_loc', 's_log_loc']]
loc_plots = hv.Overlay(curves).opts(legend_position='top', width=320)
curves = [hv.Curve(param_evolution[name], 
                   'Epoch', 'Scales', label=name) for name in ['b_scale', 'w_scale', 's_log_scale']]
scale_plots = hv.Overlay(curves).opts(legend_position='top', width=320)
loc_plots + scale_plots

Tip

When learning more complex models on larger datasets we should consider partitioning the dataset into training and validation subsets to verify ELBO convergence (early stopping).

Inspecting the posterior

The Predictive object from numpyro.infer can be used to obtain the posterior of the parameters and the predictive posterior over new test data

Instead of passing posterior_samples (as in MCMC) we pass the guide function and the learned parameters

predictive = numpyro.infer.Predictive(model, 
                                      guide=svi.guide, 
                                      params=svi.get_params(state), 
                                      return_sites=['w', 'b', 's_eps', 'mu'],
                                      num_samples=1000)

x_test = jnp.linspace(-12, 12, num=100)
posterior_samples = predictive(random.PRNGKey(1), x_test)

def plot_marginals(posterior_samples):
    dist_w = hv.Distribution(posterior_samples['w'], 'w') * hv.VLine(w_true) 
    dist_b = hv.Distribution(posterior_samples['b'], 'b') * hv.VLine(b_true) 
    dist_s = hv.Distribution(posterior_samples['s_eps'], 's_eps') * hv.VLine(s_true) 
    return dist_b + dist_w + dist_s

plot_marginals(posterior_samples)

def plot_joint_posterior(posterior_samples, param1, param2):
    posterior = hv.Bivariate(jnp.stack((posterior_samples[param1], posterior_samples[param2])).T, 
                             kdims=[param1, param2])
    return posterior.opts(cmap='Blues', line_width=0,
                          filled=True, width=300, axiswise=True)

hv.Layout([plot_joint_posterior(posterior_samples, 'w', 'b'),
           plot_joint_posterior(posterior_samples, 's_eps', 'b'),
           plot_joint_posterior(posterior_samples, 's_eps', 'w')
          ])

Note

Remember we used a factored normal guide, we expect no correlations

def plot_predictive(posterior_samples):
    low, mid, upper = jnp.quantile(posterior_samples['mu'], jnp.array([0.01, 0.5, 0.99]), axis=0)
    median = hv.Curve((x_test, mid)).opts(width=500, color='#30a2da')
    data = hv.ErrorBars((x, y, s_true))
    uncertainty = hv.Area((x_test, low, upper), vdims=['y', 'y2']).opts(color='#30a2da', alpha=0.3)
    return median * data * uncertainty

plot_predictive(posterior_samples)

Autoguides

Given a model, numpyro offers functions to generate guides automatically from it. These are found at numpyro.infer.autoguide

Note

The guide we previously wrote is roughly equivalent to AutoDiagonalNormal/AutoNormal, a guide where the latent variables are normal and independent

Other interesting auto guides are

  • AutoMultivariateNormal: Models correlation between the latent variables

  • AutoLowRankMultivariateNormal: Similar to the previous one, but using a low rank covariance matrix. Consider it when latent dimensionality is large

  • AutoDelta: Returns the Maximum a Posteriori estimate

  • AutoLaplaceApproximation: Multivariate normal guide centered on the MAP with variance equal to the negative hessian

  • AutoIAFNormal: Uses a sequence of bijective transformations starting from a Gaussian to obtain a more flexible distribution (more in this in future lessons)

The arguments of an AutoGuide are

  • A numpyro model

  • prefix (Optional): A string to name the internal parameters

  • init_loc_fn(Optional): An initialization scheme

Let’s see some examples

from numpyro.infer.autoguide import AutoDelta, AutoMultivariateNormal

%%time
key, key_ = random.split(key)  
svi, state, loss_evolution, param_evolution = train_svi(AutoDelta(model, prefix='MAP'), 
                                                        key_, nepochs=300)    

['b_MAP_loc', 's_eps_MAP_loc', 'w_MAP_loc']

CPU times: user 3.49 s, sys: 13.3 ms, total: 3.5 s
Wall time: 3.51 s

hv.Curve(loss_evolution, 'Epoch', 'Loss').opts(width=500, logy=True)

svi.get_params(state)

{'b_MAP_loc': DeviceArray(-0.7979058, dtype=float32),
 's_eps_MAP_loc': DeviceArray(0.7400651, dtype=float32),
 'w_MAP_loc': DeviceArray(0.52685213, dtype=float32)}

predictive = numpyro.infer.Predictive(model, 
                                      guide=svi.guide, 
                                      params=svi.get_params(state), 
                                      return_sites=['w', 'b', 's_eps', 'mu'],
                                      num_samples=1000)

x_test = jnp.linspace(-12, 12, num=100)
posterior_samples = predictive(random.PRNGKey(1), x_test)

plot_predictive(posterior_samples)

Note

The AutoDelta guide returns point estimates (MAP)

%%time
key, key_ = random.split(key)  
svi, state, loss_evolution, param_evolution = train_svi(AutoMultivariateNormal(model, prefix='MVN'), 
                                                        key_, nepochs=4000)

['MVN_loc', 'MVN_scale_tril']

CPU times: user 29.5 s, sys: 180 ms, total: 29.7 s
Wall time: 29.6 s

hv.Curve(loss_evolution, 'Epoch', 'Loss').opts(width=500, logy=True)

predictive = numpyro.infer.Predictive(model, 
                                      guide=svi.guide, 
                                      params=svi.get_params(state), 
                                      return_sites=['w', 'b', 's_eps', 'mu'],
                                      num_samples=1000)

x_test = jnp.linspace(-12, 12, num=100)
posterior_samples = predictive(random.PRNGKey(1), x_test)

plot_marginals(posterior_samples)

hv.Layout([plot_joint_posterior(posterior_samples, 'w', 'b'),
           plot_joint_posterior(posterior_samples, 's_eps', 'b'),
           plot_joint_posterior(posterior_samples, 's_eps', 'w')
          ])

Note

The AutoMultivariateNormal guide models the correlation between \(b\) and \(w\)

plot_predictive(posterior_samples)

See also

See pyro’s tips and tricks for SVI, they apply to numpyro

previous

Approximate Inference

next

Recent advances on VI