Contents

Linear Latent Variable Models

Linear Latent Variable Models

Modeling with latent variables

Let’s say we have a dataset \(X = \{ \textbf{x}_1, \textbf{x}_2, \ldots, \textbf{x}_N\}\) with \(\dim (\textbf{x}) =D\) and we want to model the generative distribution \(p(\textbf{x})\)

Each sample has \(D\) components or attributes (e.g. the pixels of an image): These are the observed variables

To model \(p(\textbf{x})\) we may expand the joint probability between the attributes using the rules of probability

\[ p(x_1, x_2, \ldots, x_D) = p(x_D|x_{D-1}, \ldots, x_1) \cdot p(x_{D-1}| , x_{D-1}\ldots, x_1) \cdots p(x_3|x_1, x_1) \cdot p(x_2|x_1) \cdot p(x_1) \]

which is known as a fully observed model

Warning

Unless we introduce independence between some of the variables the above representation is impractical for high dimensional problems (e.g. images)

Hint

Assume that what we observe is correlated due to hidden causes

These hidden causes are represented as latent variables and models with latent variables are called Latent Variable Models (LVMs)

Mathematically, we impose that the observed variables are conditionally independent given the latent variables \(\textbf{z}\), this is

\[ p(x_1, x_2, \ldots, x_D|\textbf{z}) = p(x_D|\textbf{z}) \cdot p(x_{D-1}|\textbf{z}) \cdots p(x_3|\textbf{z}) \cdot p(x_2|\textbf{z}) \cdot p(x_1|\textbf{z}) \]

where in general \(\dim(\textbf{z})\ll\dim(\textbf{x})\)

The following figure shows the graphical model of a fully observed model with five observed variables and an LVM with two latent variables

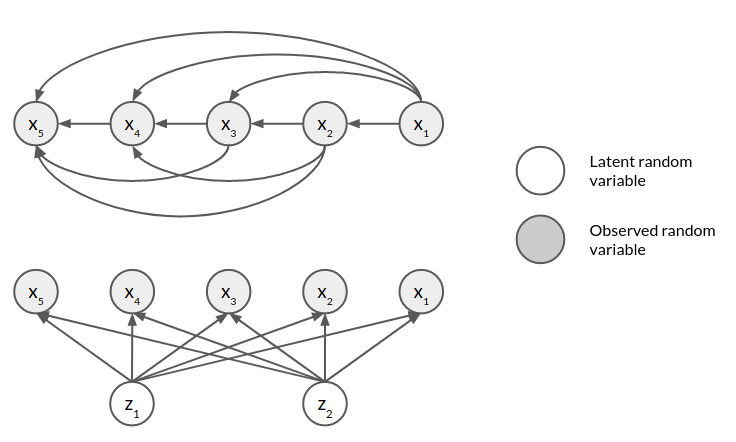
../../_images/LVM.png

For the LVM we can write the marginal as

\[\begin{split} \begin{align} p(\textbf{x}) &= \int_z p(\textbf{x}, \textbf{z}) \,d\textbf{z} \nonumber \\ &= \int_\textbf{z} p(\textbf{x}|\textbf{z}) p(\textbf{z}) \,d\textbf{z} \nonumber \end{align} \end{split}\]

Did we gain anything? (YES)

Important

This strategy allows us to model a complex \(p(x)\) by proposing a simple \(p(z)\) (easy to sample from) and a transformation \(p(x|z)\)

The integral above is intractable for non-linear transformations (neural networks), in that case we resort to approximate inference

This lecture is focused on LVMs for continuous data. First we will review an example with a tractable posterior (PCA) and then the more modern LVM based on neural networks: The Variational Autoencoder

A short review of PCA

Principal Component Analysis (PCA) is an algorithm to reduce the dimensionality of continous data

For a dataset \(X = (x_1, x_2, \ldots, x_N) \in \mathbb{R}^{N \times D}\), in PCA we

  1. Compute covariance matrix \(C = \frac{1}{N} X^T X\)

  2. Solve the eigenvalue problem \((C - \lambda I)W = 0\)

This comes from the following objective

\[ \max_W W^T C W, \text{s.t.} ~ W^T W = I, \]

i.e. PCA finds an orthogonal transformation \(W\) that maximizes the variance of the projected data \(XW\)

Important

By reducing the amount of columns of \(W\) we reduce the dimensionality of \(XW\)

Example: Classical PCA for MNIST using JAX

We will use the MNIST handwritten digits dataset:

import os
import sys
sys.path.append(os.path.abspath(os.path.join('../utils')))
from mnist import mnist
train_images, train_labels, test_images, test_labels = mnist()

import holoviews as hv
hv.extension('bokeh')
hv.opts.defaults(hv.opts.Image(cmap='gray', xaxis=None, yaxis=None))

examples = [hv.Image(example.reshape(28, 28)) for example in test_images[:10]]
hv.Layout(examples).opts(hv.opts.Image(width=100, height=100)).cols(5)

Implementation of PCA using jax.numpy.eigh:

import numpy as np
import jax.numpy as jnp

class PCA:
    def __init__(self, data, K=2):
        self.data_mean = data.mean(axis=0)
        data_centered = data - self.data_mean
        C = jnp.dot(data_centered.T, data_centered)
        L, W = jnp.linalg.eigh(C, symmetrize_input=False)
        # eigh, returns sorted by L (eigenvals) in ascending order
        self.L = L[-K:]
        self.W = W[:, -K:]
        
    def get_eigenvalues(self):
        return self.L
    
    def encode(self, x):
        return jnp.dot(x - self.data_mean, self.W)
    
    def decode(self, z):
        return self.data_mean + jnp.dot(z, self.W.T)

In this example the \(28\times28\) observed dimensions of PCA are projected to two continuous latent variables

pca = PCA(train_images, K=2)
z = pca.encode(test_images)
xhat = pca.decode(z)
z

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

DeviceArray([[-2.9325423 ,  1.3030709 ],
             [ 3.747396  , -0.08111978],
             [ 1.6895869 ,  3.7099552 ],
             ...,
             [-2.3406672 ,  1.0596066 ],
             [ 0.42589757,  1.2315243 ],
             [ 0.35495937, -4.087756  ]], dtype=float32)

We can then inspect the latent space and images reconstructed from it

scatter_plot = []
for digit in range(10):
    mask = test_labels.argmax(axis=1) == digit
    scatter_plot.append(hv.Scatter((z[mask, 0], z[mask, 1]), 'z0', 'z1', label=f"{digit}"))
    
hv.Overlay(scatter_plot).opts(width=550, height=400, legend_position='right')

examples = [hv.Image(example.reshape(28, 28)) for example in test_images[:5]]
reconstructed = [hv.Image(example.reshape(28, 28)) for example in np.array(xhat[:5])]

hv.Layout(examples + reconstructed).opts(hv.opts.Image(width=100, height=100)).cols(5)

The two most important principal components in this case are

eigvectors = [hv.Image(np.array(eigvec.reshape(28, 28))) for eigvec in pca.W.T]
hv.Layout(eigvectors).opts(hv.opts.Image(width=200, height=200))

Note

Clearly wwo continous latent variables are not enough to model the digits given this linear model. Later we will see how this changes using non-linear models

Probabilistic interpretation for PCA

We can give a probabilistic interpretation to PCA as an LVM

The observed data \(x_i \in \mathbb{R}^D\) is modeled as

\[ x_i = W z_i + B + \epsilon, ~i=1,\ldots,N \]

where

  • \(B \in \mathbb{R}^D\) is the mean of \(X\)

  • \(W \in \mathbb{R}^{D\times K}\) is a linear transformation matrix

  • \(\epsilon\) is a noise vector

  • \(z_i \in \mathbb{R}^K\) is a continuous latent variable with \(K\ll D\)

Note

\(x\) (observed) is related to \(z\) (latent) via a linear mapping

The PCA model has the following assumptions

  1. The noise is independent and Gaussian distributed with variance \(\sigma^2\)

  2. The latent variable has a standard Gaussian prior

Using these we can write

\[ p(x_i | z_i) = \mathcal{N}(B + W z_i, I \sigma^2) \]

and

\[ p(z_i) = \mathcal{N}(0, I) \]

Given that the Gaussian is conjugate to itself the marginal likelihood is

\[\begin{split} \begin{split} p(x) &= \int p(x|z) p(z) \,dz \\ &= \mathcal{N}(x|B, W W^T + I\sigma^2 ) \end{split} \end{split}\]

Note

We have parameterized a Gaussian with full covariance from two Gaussians with diagonal covariance

::

The parameters of the marginal come from

  • \(\mathbb{E}[x] = W\mathbb{E}[z] + B + \mathbb{E}[\epsilon] = B\)

  • \(\mathbb{E}[(Wz + \epsilon)(Wz + \epsilon)^T] = W \mathbb{E}[zz^T] W^T + \mathbb{E}[\epsilon \epsilon^T] = W W^T + I\sigma^2\)

The posterior

Using this formalism we can write the posterior as

\[ p(z|x) = \mathcal{N}(z|M^{-1}W^T(x-B), M\sigma^{-2} ) \]

which can be used to move from observed to latent dimension, where

\[ M = W^T W + I\sigma^2 \]

Training

We find \(W\), \(B\) and \(\sigma\) that best fit the data by maximizing the log marginal likelihood

\[ \hat W, \hat B, \hat \sigma^2 = \text{arg} \max_{W, B, \sigma^2} \sum_{i=1}^N \log p(x_i) \]

which has a closed form analytical solution.

Note

The solution for \(W\) is equivalent to conventional PCA (\(\sigma^2 \to 0\)). The main difference is that we have \(\sigma\) and we can generate data with \(p(x|z)p(z)\)

See also

For more details on PCA and probabilistic PCA see chapters 15 and 21 in D. Barber’s book

previous

Bayesian Linear Regression

next

An theoretical introduction to Gaussian processes