Contents

An theoretical introduction to Gaussian processes

An theoretical introduction to Gaussian processes

Motivation

Before training a neural network (deterministic or probabilistic) we have to select its architecture. For example, in the case of a multilayer perceptron (MLP), we need to choose the number of layers (depth) and the number of nodes (neurons) per layer (width)

Important

With this we are defining the neural network as a function with fixed structure

Increasing the width and depth gives the model more flexibility. But in general, we don’t know “how much flexibility” is needed for a particular problem

Note

The architecture is a collection of hyper-parameters

The good (and typical) practice is to find the “best structure” using a validation (holdout) dataset. But what if, instead of testing several architectures, we use a (non-parametric) model with no fixed structure?

This lesson presents the Gaussian Process (GP), a bayesian non-parametric model that can be seen as a neural network with one hidden layer and potentially infinite width

Note

In general, non-parametric models automatically grow in complexity (width) with data

Note that non-parametric models do have prior distributions and tunable hyper-parameters. The difference is that the distribution of its parameters lives in an infinite dimensional space. We use non-parametric models by integrating out (marginalizing) this infinite distribution

See also

Other non-parametric models not covered in this lesson are the many variants of the

  • Dirichlet Process

  • infinite Hidden Markov Model

  • Indian Buffer Process

See Zhoubin Ghahramadi’s tutorial for a presentation of these methods

Defining the Gaussian process

Consider the probabilistic linear regression problem from previous lessons

\[ y_i = \sum_{k=1}^M \phi_k(x_i) \theta_k + \epsilon_i \quad \forall i=1,2,\ldots,N \]

where \(\epsilon_i\) is iid Gausian and \(\phi_k\) is a collection of \(M\) (non-linear) basis functions

We can write this in matrix form as

\[ Y = \Phi(X) \theta + E \]

where \(E\) is a diagonal matrix and \(\Phi(X) \in \mathbb{R}^{N \times M}\)

Let’s set a Gaussian prior for \(\theta\) :

\[ p(\theta) = \mathcal{N}(0, \sigma_\theta^2 I) \]

What is the distribution of \(f_\theta(X) = \Phi(X) \theta\) in this case? If \(\Phi\) is a deterministic transformation then the distribution of \(f\) is also Gaussian

By our previous definitions, the mean of \(p(f)\) is

\[ \mathbb{E}[f_\theta(X)] = \Phi(X)\mathbb{E}[\theta] = 0 \]

and its covariance is

\[ \mathbb{E}[ f_\theta(X) f_\theta(X)^T] = \Phi(X)\mathbb{E}[\theta \theta^T ] \Phi(X)^T = \sigma_\theta^2 \Phi(X) \Phi(X)^T = K \]

where \(K \in \mathbb{R}^{N\times N}\) is a symmetric and positive-definite matrix called the Gram matrix or Gramian matrix.

The \(ij\)-th element of the gram matrix is

\[ K_{ij} = \sum_{k=1}^M \phi_k(x_i) \phi_k(x_j) = \left \langle \vec \phi(x_i) , \vec \phi(x_j) \right \rangle = \kappa(x_i, x_j) \]

where \(\kappa(\cdot, \cdot): \mathcal{X} \times \mathcal{X} \to \mathbb{R}\) is called the kernel. In general we will forget about \(\{\phi_k(\cdot)\}\) and work only with the kernel.

With all these we can finally write

\[ p(f) = \mathcal{N}(0, K) \]

which is a “prior over functions”.

Note

We have dropped the dependence on \(\theta\)

Important

\(f\) is a multivariate random variable (random process) with joint Gaussian distribution: \(f\) is a Gaussian Process

Inference with a GP

Consider a dataset \(\textbf{x}=(x_1, x_2)\), \(\textbf{y}=(y_1, y_2)\). With this dataset we are interested in predicting (inferring) for a new observation \(x^*\): \(f(x^*)\) or \(f^*\) for short. This corresponds to the posterior \(p(f^*|\textbf{y}, \textbf{x}, x^*)\)

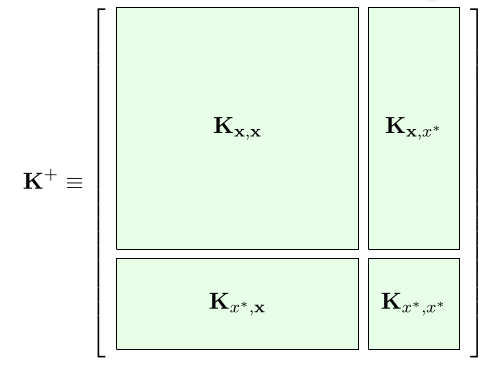
As before we can write the joint (Gaussian) distribution between the dataset and the new sample as

\[ p(\textbf{y}, f^*|\textbf{x}, x^*) = \mathcal{N}(0, K^+) \]

where

\[\begin{split} K^+ = \begin{pmatrix} K_{\textbf{x}\textbf{x}} + \sigma_\epsilon^2 I & K_{\textbf{x}x^*} \\ K_{\textbf{x}x^*}^T & K_{x^*x^*} \end{pmatrix} \end{split}\]

is a block matrix and

\[\begin{split} K_{\textbf{x}\textbf{x}} = \begin{pmatrix} \kappa(x_1, x_1) & \kappa(x_1, x_2) \\ \kappa(x_1, x_2) & \kappa(x_2, x_2)\end{pmatrix}, \quad K_{\textbf{x}x^*} = \begin{pmatrix} \kappa(x_1, x^*) \\ \kappa(x_2, x^*) \end{pmatrix} \end{split}\]

The Gaussian distribution is closed under conditioning, i.e. if we have a joint gaussian distribution the conditional distribution of a variable given the others is gaussian (nice step by step example). Here we use this property to write

\[\begin{split} \begin{split} p(f^*|\textbf{y}, \textbf{x}, x^*) = \mathcal{N}(&K_{\textbf{x}x^*} (K_{\textbf{x}\textbf{x}}+I\sigma_\epsilon^2)^{-1} \textbf{y}, \\ & K_{x^*x^*} - K_{\textbf{x}x^*} (K_{\textbf{x}\textbf{x}}+I\sigma_\epsilon^2)^{-1} K_{\textbf{x}x^*}^T ) \end{split} \end{split}\]

which gives us the result we seek

We can use Gaussian conditioning to predict on several “new data points” at the same time, we only need to compute the sub gram matrices between and within the training set and the test set

../../_images/gram_matrix_block.png

The kernel

The GP is mainly defined by its covariance also known as the gram matrix

\[\begin{split} K = \begin{pmatrix} \kappa(x_1, x_1)& \kappa(x_1, x_2)& \ldots & \kappa(x_1, x_N) \\ \kappa(x_2, x_1)& \kappa(x_2, x_2)& \ldots & \kappa(x_2, x_N) \\ \vdots& \vdots& \ddots & \vdots \\ \kappa(x_N, x_1)& \kappa(x_N, x_2)& \ldots & \kappa(x_N, x_N) \\ \end{pmatrix} \end{split}\]

where the following relation between the kernel and the basis function

\[ \kappa(x_i, x_j) = \left \langle \vec \phi(x_i) , \vec \phi(x_j) \right \rangle \]

is known as the “kernel trick”.

Before we defined a finite dimensional \(\vec \phi\) and obtained \(\kappa\). But in general it is more interesting to skip \(\phi\) and design \(\kappa\) directly. We only need \(\kappa\) to be a symmetric and positive-definite function

The broadly used Gaussian kernel complies with these restrictions

\[ \kappa(x_i, x_j) = \sigma^2 \exp \left ( \frac{\|x_i - x_j \|^2}{2\ell^2} \right) \]

where hyperparameter \(\sigma\) controls the amplitude and \(\ell\) controls the length-scale of the interactions between samples.

Using a taylor expansion we can show that the (non-linear) basis function of this kernel is

\[ \phi(x) = \lim_{M\to\infty} \sigma^2 \exp\left({-\frac{\|x\|^2}{2\ell^2}}\right) \begin{pmatrix} 1 & \frac{x}{\ell} & \frac{x^2}{\ell^2 \sqrt{2}} & \cdots & \frac{x^M}{\ell^M \sqrt{M!}} \end{pmatrix} \]

i.e. the Gaussian kernel induces an infinite-dimensional basis function.

Note

A Gaussian process with Gaussian kernel has an implicit infinite dimensional parameter vector \(\theta\)

We are not anymore explicitely choosing the structure of the function, but by selecting a kernel we are choosing a general “behavior”. For example, the Gaussian kernels encodes the property of locality, i.e. closer data samples should have similar predictions.

Several other valid kernels exist which encode other properties such as trends and periodicity. The following picture from Mackay’s book shows some of them:

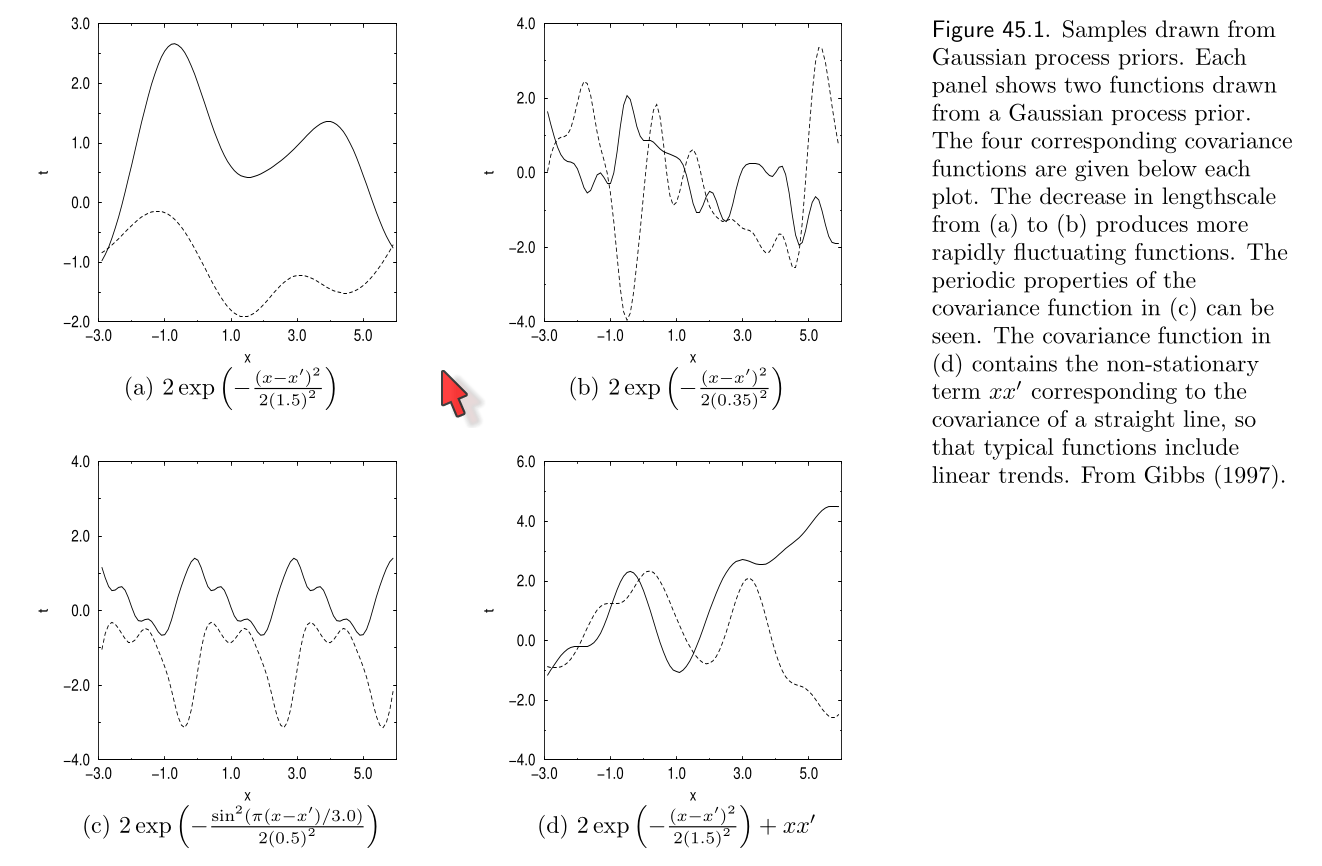
../../_images/kernels_mackay.png

  • The top plots are Gaussian kernels with different lengthscales

  • The bottom left plot is a periodic kernel

  • The bottom right plot is a Gaussian kernel plus a linear kernel

Note

Sums of products of valid kernels are also valid kernels

“Training” the GP

Fitting a GP to a dataset corresponds to finding the best combination of kernel hyperparameters which can be done by maximizing the marginal likelihood

For regression with iid Gaussian noise the marginal likelihood \(y\) is also Gaussian

\[ p(\textbf{y}|\textbf{x}) = \int p(\textbf{y}|f) p(f) \,df = \mathcal{N}(0, K + \sigma_\epsilon^2 I ) \]

where the hyperparameter \(\sigma_\epsilon^2\) is the variance of the noise

Note

It is equivalent and much easier to maximize the log marginal likelihood:

\[ \log p(\textbf{y}|\textbf{x}) = -\frac{1}{2} \textbf{y}^T (K + \sigma_\epsilon^2I)^{-1} \textbf{y} - \frac{1}{2} \log | 2\pi (K + \sigma_\epsilon^2I) | \]

from which we compute derivatives to update the hyperparameters through gradient descent

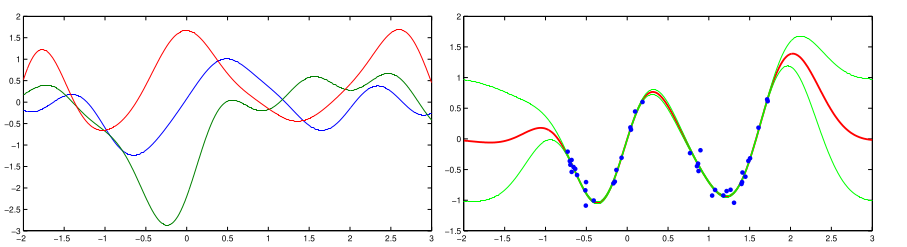
The following picture from Barber’s book shows three examples drawn from the GP prior (gaussian kernel) on the left and the mean/variance of the GP posterior after training on the right

../../_images/gp_fitted.png

Relation between GPs and Neural Networks

(Neil 1994) showed that a fully connected neural network with one hidden layer tends to a Gaussian process in the limit of infinite hidden units as a consequence of the central limit theorem. The following shows a mumary of the proof

More recently, several works have explored the relationship between GPs and Deep Neural Networks:

See also

For more on GP please see

previous

Linear Latent Variable Models

next

Approximate Inference