Caminatas aleatorias
Contenido
import holoviews as hv
hv.extension('bokeh')
hv.opts.defaults(hv.opts.Curve(width=500),
hv.opts.HLine(alpha=0.5, color='r', line_dash='dashed'))
import random
import numpy as np
import scipy.stats
4. Caminatas aleatorias¶
La caminata aleatoria es un modelo ampliamente utilizando con aplicaciones en ecología, física, economía, entre otros. A continuación algunos ejemplos
El precio de las acciones de una firma
En la actividad asociada a esta lección veremos como podemos aplicarlo en un contexto económico.
4.1. Definición¶
Una caminata aleatoria es una secuencia de pasos o movimientos que se escogen aleatoriamente dentro de un cierto espacio.
Considere por ejemplo el espacio de los enteros en una dimensión
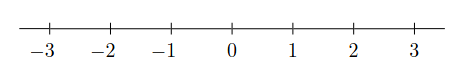
Digamos que inicialmente estamos en la posición \(0\) y que en cada paso lanzamos una moneda. Si sale cara nos movemos a la derecha (\(+1\)), si sale sello nos movemos a la izquierda (\(-1\)). Dadas estas reglas
¿Dónde estoy luego de lanzar \(r\) veces la moneda?
Podemos definir la posición luego de lanzar \(i+1\) veces la moneda como
donde \(m \in \{0, 1\}\) es una variable aleatoria que se distribuye Bernoulli
y donde estamos asumiendo una moneda “justa”, es decir con probabilidad \(0.5\).
Importante
Esta distribución define las “transiciones” o pasos de la caminata
Más adelante veremos como responder una pregunta como la planteada utilizando una simulación de Monte Carlo sobre el modelo de caminata aleatoria.
4.2. Proceso estocástico y propiedad de Markov¶
Una caminata aleatoria es un tipo particular de proceso estocástico. Llamamos proceso estocástico a una colección de variables aleatorias ordenadas como una secuencia
Por ejemplo
es una secuencia de variables aleatorias indexadas en el tiempo o
es una secuencia de variables aleatorias con un índice discreto
Una caminata aleatoria es además un caso particular de proceso Markoviano. La propiedad de Markov dice que el lugar donde estaré en el futuro sólo depende de donde estoy en el presente. No hay dependencia del pasado. Esto se resume matematicamente como:
En una próxima lección estudiaremos en detalle las cadenas de Markov
4.3. Ejemplo: Caminata en dos dimensiones¶
Sea un espacio discreto en dos dimensiones y un personaje que parte en la posición \((0, 0)\).
El personaje puede moverse hacia el Norte, Sur, Este o Oeste.
La probabilidad de escoger cada una de estas direcciones es \(1/4\)
En promedio
¿A qué distancia del centro estará el personaje luego de \(10\), \(100\) y \(1000\) pasos?
Respondamos esta pregunta usando una simulación de Monte Carlo.
Primero escribimos una función que recibe una cantidad de pasos y retorna una arreglo con las posiciones del personaje en cada instante. La decisión aleatoria de la dirección la tomaremos en usando la función np.random.choice
def caminata_bidimensional(pasos):
probs = np.array([1/4, 1/4, 1/4, 1/4])
direcciones = np.array([[0, 1], [1, 0], [-1, 0], [0, -1]])
posicion = np.zeros(shape=(pasos+1, 2))
decisiones = np.random.choice(len(probs), size=pasos, p=probs)
desplazamientos = direcciones[decisiones, :]
posicion[1:, :] = np.cumsum(desplazamientos, axis=0)
return posicion
La siguiente gráfica muestra el recorrido y destino final del personaje
np.random.seed(0)
pos = caminata_bidimensional(100)
p_recorrido = hv.Curve((pos[:, 0], pos[:, 1])).opts(xlim=(-15, 15), ylim=(-15, 15))
p_destino = hv.Points((pos[-1, 0], pos[-1, 1])).opts(size=10)
hv.Overlay([p_recorrido, p_destino])
Respondamos ahora la pregunta usando Montecarlo. Utilizaremos la distancia de Manhattan para medir la distancia al centro del mapa
def distancia_manhattan(posicion):
return np.sum(np.absolute(posicion[-1, :]))
repeticiones = 1000
print("En promedio...")
for pasos in [10, 100, 1000]:
distancias = np.empty(shape=(repeticiones,))
for i in range(repeticiones):
distancias[i] = distancia_manhattan(caminata_bidimensional(pasos))
print(f"...luego de {pasos} pasos, el personaje está a {np.mean(distancias)} del centro del mapa")
En promedio...
...luego de 10 pasos, el personaje está a 3.504 del centro del mapa
...luego de 100 pasos, el personaje está a 11.334 del centro del mapa
...luego de 1000 pasos, el personaje está a 35.194 del centro del mapa
¿Cómo cambia el resultado con el número de repeticiones para el caso de 100 pasos?
Ns = np.logspace(0, 4, 10)
stats = np.zeros(shape=(len(Ns), 3))
pasos = 100
for k, repeticiones in enumerate(Ns):
repeticiones = int(repeticiones)
distancias = np.empty(shape=(repeticiones,))
for i in range(repeticiones):
distancias[i] = distancia_manhattan(caminata_bidimensional(pasos))
stats[k, :] = np.percentile(distancias, (25, 50, 75))
La siguiente gráfica muestra la mediana y el rango intercuartial de las simulaciones a medida que aumentan las repeticiones. La linea roja puntada corresponde a la raíz cuadrada del número de pasos
p_med = hv.Curve((Ns, stats[:, 1]), 'Repeticiones', 'Distancia al centro', label='Mediana').opts(logx=True)
p_iqr = hv.Area((Ns, stats[:, 0], stats[:, 2]), vdims=['y', 'y2'], label='IQR').opts(alpha=0.25)
hv.Overlay([p_med, p_iqr, hv.HLine(np.sqrt(pasos))])
4.4. Actividad formativa: Jugando a la ruleta¶

(Moraleja: la casa siempre gana)
Sea un casino con una ruleta con 36 casilleros numerados del 1 al 36
Una persona llega al casino y comienza a jugar ruleta. Su estrategia de juego es siempre
Jugar la primera apuesta a los pares
Luego apostarle \(1.000\) pesos a los números pares si el resultado anterior fue impar
O apostarle \(1.000\) pesos a los números impares si el resultado anterior fue par
En promedio:
¿Cuánto podría ganar/perder esta persona con su particular estrategia?
Utilizemos una simulación de Monte Carlo para resolverlo. En primer lugar escribiremos una clase Ruleta con los métodos girar y apostar. Para seleccionar un casillero de forma aleatoria utilizaremos la función choice de la librería random de Python
class Ruleta():
def __init__(self):
self.casilleros = []
for i in range(1, 36+1):
self.casilleros.append(i)
def _girar(self):
return random.choice(self.casilleros)
def apostar(self, apuestas, cantidad):
bola = self._girar()
if bola in apuestas:
ganancia = 36/len(apuestas)
else:
ganancia = 0
return cantidad*(ganancia - 1), bola
Simulemos 10 sesiones de juego bajo las condiciones anteriores. En el gráfico:
Las lineas de colores correspondan a la ganancia en cada una de las sesiones.
La linea negra corresponda al promedio de las sesiones.
random.seed(12345)
casino_dreams = Ruleta()
simulaciones = []
giros = 1000
dinero_apuesta = 1_000
pares = [x for x in range(2, 37, 2)]
impares = [x for x in range(1, 37, 2)]
for k in range(10):
retornos = np.zeros(shape=(giros,))
# La primera apuesta es a par
retornos[0], bola = casino_dreams.apostar(pares, dinero_apuesta)
# Las apuestas siguientes dependen del resultado anterior de la ruleta
for i in range(1, giros):
if bola in pares:
retornos[i], bola = casino_dreams.apostar(impares, dinero_apuesta)
elif bola in impares:
retornos[i], bola = casino_dreams.apostar(pares, dinero_apuesta)
simulaciones.append(np.cumsum(retornos))
simulaciones = np.vstack(simulaciones)
p = []
for retornos_acumulados in simulaciones:
p.append(hv.Curve((retornos_acumulados), 'Apuestas', 'Retorno acumulado [$]'))
hv.Overlay(p) * hv.HLine(0) * hv.Curve((np.mean(simulaciones, axis=0))).opts(color='k')
Nota
En promedio el retorno está en torno a cero. Al parecer la estrategia no es muy efectiva.
Una ruleta de casino tiene además dos casilleros de color verde denominados “0” y “00”. Si la bola cae en uno de estos casilleros la casa se lleva todo. ¿Cómo cambia el resultado anterior si agregamos estos casilleros?
Regla adicional para la estrategia del jugador:
En caso de observar ‘0’ o ‘00’ entonces el jugador mantiene su apuesta anterior
class RuletaRealista(Ruleta):
def __init__(self):
super().__init__()
self.casilleros.append(0) # Representa el cero
self.casilleros.append(-1) # Represeta el doble cero
random.seed(12345)
casino_dreams = RuletaRealista()
simulaciones = []
giros = 1000
dinero_apuesta = 1_000
pares = [x for x in range(2, 37, 2)]
impares = [x for x in range(1, 37, 2)]
for k in range(10):
retornos = np.zeros(shape=(giros,))
# La primera apuesta es a par
retornos[0], bola = casino_dreams.apostar(pares, dinero_apuesta)
last_bet = pares
# Las apuestas siguientes dependen del resultado anterior de la ruleta
for i in range(1, giros):
if bola in pares:
last_bet = impares
elif bola in impares:
last_bet = pares
retornos[i], bola = casino_dreams.apostar(last_bet, dinero_apuesta)
simulaciones.append(np.cumsum(retornos))
simulaciones = np.vstack(simulaciones)
p = []
for retornos_acumulados in simulaciones:
p.append(hv.Curve((retornos_acumulados), 'Apuestas', 'Retorno acumulado [$]'))
hv.Overlay(p) * hv.HLine(0) * hv.Curve((np.mean(simulaciones, axis=0))).opts(color='k')
Nota
El promedio es claramente inferior a cero, con estos nuevos casilleros en promedio “la casa gana”
Reflexione acerca de la estrategia que utilizó el jugador. Luego revise la muy famosa falacia del apostador