5. Cadenas de Markov¶

En la lección anterior vimos caminatas aleatorias y definimos lo que es un proceso estocástico. En lo que sigue nos restringiremos a procesos estocásticos que sólo puede tomar valores de un conjunto discreto \(\mathcal{S}\) en tiempos \(n>0\) que también son discretos.

Llamaremos a \(\mathcal{S}=\{1, 2, \ldots, M\}\) el conjunto de estados del proceso. Cada estado en particular se suele denotar por un número natural.

Recordemos que para que un proceso estocástico sea considerado una cadena de Markov se debe cumplir

\[ P(X_{n+1}|X_{n}, X_{n-1}, \ldots, X_{1}) = P(X_{n+1}|X_{n}) \]

que se conoce como la propiedad de Markov o propiedad markoviana.

Importante

En una cadena de markov el estado futuro es independiente del pasado cuando conozco el presente

5.1. Matriz de transición de una cadena de Markov¶

Si la cadena de Markov tiene estados discretos y es homogenea, podemos escribir

\[ P(X_{n+1}=j|X_{n}=i) = P_{ij}, \]

donde homogeneo quiere decir que la probabilidad de transicionar de un estado a otro no cambia con el tiempo. La probabilidad \(P_{ij}\) se suele llamar probabilidad de transición “a un paso”.

El conjunto con todas las posibles combinaciones \(P_{ij}\) para \(i,j \in \mathcal{S}\) forma una matriz cuadrada de \(M \times M\) que se conoce como matriz de transición

\[\begin{split} P = \begin{pmatrix} P_{11} & P_{12} & \ldots & P_{1M} \\ P_{21} & P_{22} & \ldots & P_{2M} \\ \vdots & \vdots & \ddots & \vdots \\ P_{M1} & P_{M2} & \ldots & P_{MM}\end{pmatrix} \end{split}\]

donde siempre se debe cumplir que las filas sumen 1

\[ \sum_{j \in \mathcal{S}} P_{ij} = 1, \quad \forall i \]

y además todos los \(P_{ij} \geq 0\) y \(P_{ij} \in [0, 1]\).

Una matriz de transición puede representarse como un grafo dirigido donde los vertices son los estados y las aristas las probabilidades de transición o pesos.

El siguiente es un ejemplo de grafo para un sistema de cuatro estados con todas sus transiciones equivalentes e iguales a \(1/2\). Las transiciones con probabilidad \(0\) no se muestran.

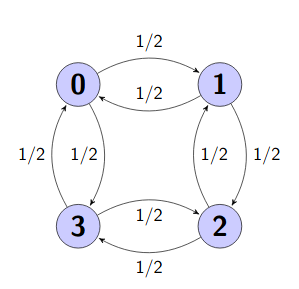
Considere ahora el siguiente ejemplo

Nota

Si entramos a los estados 0 o 3, ya no podemos retornar a los estados 1 y 2. Este es un ejemplo de cadena reducible.

Definiciones:

Estados transitorios o transientes: Estados a los cuales podríamos no retornar eventualmente.
Estados recurrentes: Estados a los que siempre podríamos retornar.
Cadena reducible: Cadena que tiene al menos un estado transitorio.
Cadena irreducible: Cadena donde todos sus estados son recurrentes.

Nota

Una cadena reducible puede “dividirse” para crear cadenas irreducibles.

En el ejemplo de arriba podemos separar \(\{0\}\), \(\{1,2\}\) y \(\{3\}\) en tres cadenas irreducibles 1

5.1.1. Ejemplo: Predicción de clima con cadena de dos estados¶

Digamos que queremos predecir el clima de Valdivia utilizando una cadena de Markov. Por lo tanto asumiremos que el clima de mañana es perfectamente predecible a partir del clima de hoy. Sean dos estados

\(s_A\) Lluvioso
\(s_B\) Soleado

Con probabilidades condicionales \(P(s_A|s_A) = 0.7\), \(P(s_B|s_A) = 0.3\), \(P(s_A|s_B) = 0.45\) y \(P(s_B|s_B) = 0.55\). En este caso la matriz de transición es

\[\begin{split} P = \begin{pmatrix} P(s_A|s_A) & P(s_B|s_A) \\ P(s_A|s_B) & P(s_B|s_B) \end{pmatrix} = \begin{pmatrix} 0.7 & 0.3 \\ 0.45 & 0.55 \end{pmatrix} \end{split}\]

que también se puede visualizar como un mapa de transición

Luego

Si está soleado hoy, ¿Cuál es la probabilidad de que llueva mañana, en tres dias más y en una semana más?

Utilicemos Python y la matriz de transición para responder esta pregunta. Primero escribimos la matriz de transición como un ndarray de Numpy

P = np.array([[0.70, 0.30],
              [0.45, 0.55]])

En segunda lugar vamos a crear un vector de estado inicial

s0 = np.array([0, 1]) # Estado soleado

Luego, las probabilidades para mañana dado que hoy esta soleado pueden calcularse como

\[ s_1 = s_0 P \]

que se conoce como transición a un paso

np.dot(s0, P)

array([0.45, 0.55])

La probabilidad para tres días más puede calcularse como

\[ s_3 = s_2 P = s_1 P^2 = s_0 P^3 \]

que se conoce como transición a 3 pasos. Sólo necesitamos elevar la matriz al cubo y multiplicar por el estado inicial

np.dot(s0, np.linalg.matrix_power(P, 3))

array([0.590625, 0.409375])

El pronóstico para una semana sería entonces la transición a 7 pasos

np.dot(s0, np.linalg.matrix_power(P, 7))

array([0.59996338, 0.40003662])

Notamos que el estado de nuestro sistema comienza a converger

np.dot(s0, np.linalg.matrix_power(P, 1000))

array([0.6, 0.4])

Nota

Esto se conoce como el estado estacionario de la cadena.

5.2. Estado estacionario de la cadena de Markov¶

Si la cadena de Markov converge a un estado, ese estado se llama estado estacionario. Por definición en un estado estacionario se cumple que

\[ s P = s \]

Que corresponde al problema de valores y vectores propios.

Nota

Los estados estacionarios son los vectores propios del sistema

Para el ejemplo anterior teniamos que

\[ \begin{pmatrix} s_1 & s_2 \end{pmatrix} P = \begin{pmatrix} s_1 & s_2 \end{pmatrix} \]

Que resulta en las siguientes ecuaciones

\[ 0.7 s_1 + 0.45 s_2 = s_1 \]

\[ 0.3 s_1 + 0.55 s_2 = s_2 \]

Ambas nos dicen que \(s_2 = \frac{2}{3} s_1\). Si además consideramos que \(s_1 + s_2 = 1\) podemos despejar y obtener

\(s_1 = 3/5 = 0.6\)
\(s_2 = 0.4\)

Que es lo que vimos antes. Esto nos dice que el largo plazo en un 60% de los días lloverá y en el restante 40% estará soleado

5.2.1. Generalizando el ejemplo anterior¶

Una pregunta interesante a responder con una cadena de Markov es

¿Cuál es la probabilidad de llegar al estado \(j\) dado que estoy en el estado \(i\) si doy exactamente \(n\) pasos?

Consideremos ahora la cadena de Markov homogenea del siguiente diagrama:

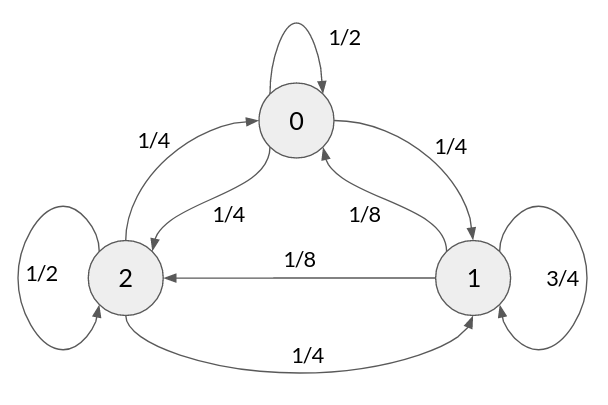
donde la matriz de transición es claramente:

\[\begin{split} P = \begin{pmatrix} 1/2 & 1/4 & 1/4 \\ 1/8 & 3/4 & 1/8 \\ 1/4 & 1/4 & 1/2\end{pmatrix} \end{split}\]

Para este ejemplo particular

¿Cúal es la probabilidad de llegar al estado \(2\) desde el estado \(0\) en 2 pasos?

Podemos resolver esto matemáticamente como

\[\begin{split} \begin{pmatrix} P_{00} & P_{01} & P_{02} \end{pmatrix} \begin{pmatrix} P_{02} \\ P_{12} \\ P_{22} \end{pmatrix} = P_{00}P_{02} + P_{01}P_{12} + P_{02}P_{22} = 0.28125 \end{split}\]

Que corresponde al elemento en la fila \(0\) y columna \(2\) de la matriz \(P^2\)

P = np.array([[1/2, 1/4, 1/4],
              [1/8, 3/4, 1/8],
              [1/4, 1/4, 1/2]])

np.dot(P, P)[0, 2]

0.28125

Importante

La probabilidad de llegar al estado \(j\) desde el estado \(i\) en \(n\) pasos es equivalente al elemento en la fila \(i\) y columna \(j\) de la matriz \(P^n\)

¿Qué ocurre cuando \(n\) tiene a infinito?

display(np.linalg.matrix_power(P, 3),
        np.linalg.matrix_power(P, 5),
        np.linalg.matrix_power(P, 100))

array([[0.2890625, 0.4375   , 0.2734375],
       [0.21875  , 0.5625   , 0.21875  ],
       [0.2734375, 0.4375   , 0.2890625]])

array([[0.25830078, 0.484375  , 0.25732422],
       [0.2421875 , 0.515625  , 0.2421875 ],
       [0.25732422, 0.484375  , 0.25830078]])

array([[0.25, 0.5 , 0.25],
       [0.25, 0.5 , 0.25],
       [0.25, 0.5 , 0.25]])

Todas las filas convergen a un mismo valor. Este conjunto de probabilidades se conoce como \(\pi\) la distribución estacionaria de la cadena de Markov. Notar que las filas de \(P^\infty\) convergen solo si la cadena es irreducible.

El elemento \(\pi_j\) (es decir \(P_{ij}^\infty\)) nos da la probabilidad de estar en \(j\) luego de infinitos pasos. Notar que el subíndice \(i\) ya no tiene importancia, es decir que el punto de partida ya no tiene relevancia.

5.3. Algoritmo general para simular una cadena de Markov discreta¶

Asumiendo que tenemos un sistema con un conjunto discreto de estados \(\mathcal{S}\) y que conocemos la matriz de probabilidades de transición \(P\) podemos simular su evolución con el siguiente algoritmo

Setear \(n=0\) y seleccionar un estado inicial \(X_n = i\)
Para \(n = 1,2,\ldots,T\)
1. Obtener la fila de \(P\) que corresponde al estado actual \(X_n\), es decir \(P[X_n, :]\)
2. Generar \(X_{n+1}\) muestreando de una distribución multinomial con vector de probabilidad igual a la fila seleccionada

En este caso \(T\) es el horizonte de la simulación. A continuación veremos como simular una cadena de Markov discreta usando Python

Digamos que tenemos una cadena con tres estados y que la fila de \(P\) asociada a \(X_n\) es \([0.7, 0.2, 0.1]\).

Podemos usar scipy.stats.multinomial para generar aleatoriamente una variable multinomial y luego aplicar el argumento máximo para obtener el índice del estado \(X_{n+1}\)

np.random.seed(12345)
for i in range(3):
    a = scipy.stats.multinomial.rvs(n=1, p=[0.7, 0.2, 0.1], size=1) 
    print(a, np.argmax(a, axis=1))

[[0 1 0]] [1]
[[1 0 0]] [0]
[[1 0 0]] [0]

Las muestras generadas por scipy.stats.multinomial.rvs son vectores en formato one-hot. Estos vectores tienen tantos componentes como estados. Tienen un sólo 1 en la posición del estado que fue seleccionado y las demás posiciones están rellenas con ceros
El argumento máximo (argmax) del vector one-hot retorna el índice del estado seleccionado

Si repetimos esto 1000 veces se obtiene la siguiente distribución para \(X_{n+1}\)

x = np.argmax(scipy.stats.multinomial.rvs(n=1, p=[0.7, 0.2, 0.1], size=1000), axis=1)
edges, bins = np.histogram(x, range=(np.amin(x)-0.5, np.amax(x)+0.5), 
                           bins=len(np.unique(x)), density=True)

hv.Histogram((edges, bins), kdims='x', vdims='Densidad').opts(xticks=[0, 1, 2])

Lo cual coincide con la fila de \(P\) que utilizamos

Ahora que sabemos como obtener el estado siguiente probemos algo un poco más complicado.

Consideremos el ejemplo de predicción de clima y simulemos 1000 cadenas a un horizonte de 10 pasos

P = np.array([[0.70, 0.30],
              [0.45, 0.55]])

n_chains = 1000
horizon = 10
states = np.zeros(shape=(n_chains, horizon+1), dtype='int')
states[:, 0] = 1 # El estado inicial para todas las cadenas es 1 (soleado: sb)

for i in range(n_chains):
    for j in range(1, horizon+1):
        states[i, j] = np.argmax(scipy.stats.multinomial.rvs(n=1, p=P[states[i, j-1], :], size=1), axis=1)[0]

A continuación se muestran las tres primeras simulaciones como series de tiempo

p =[]
for i in range(3):
    p.append(hv.Curve((states[i, :]), 'n', 'Estados', label=f'Cadena {i}').opts(yticks=[0, 1], 
                                                                                xticks=list(range(11)),
                                                                                alpha=0.75, line_width=3))
hv.Overlay(p).opts(hv.opts.Overlay(legend_position='top'))

A continuación se muestra la evolución de la probabilidad asociada a cada estado a lo largo de la cadena

n_states = len(np.unique(states))

hist = np.zeros(shape=(horizon+1, n_states))
for j in range(horizon+1):
    hist[j, :] = np.array([sum(states[:, j] == s) for s in range(n_states)])

p0 = hv.Curve((hist[:,0]/np.sum(hist,axis=1)), 'n', 'Probabilidad',label='Estado 0 (lluvioso)')
p1 = hv.Curve((hist[:,1]/np.sum(hist,axis=1)), 'n', 'Probabilidad',label='Estado 1 (soleado)')
hv.Overlay([p0, p1]).opts(legend_position='top', xticks=list(range(11)))

Las probabilidades convergen de cada estado convergen a los valores que vimos anteriormente.

5.4. Ley de los grandes números para variables no i.i.d.¶

Previamente vimos que el promedio de un conjunto de \(N\) variables independientes e idénticamente distribuidas (iid) converge a su valor esperado cuando \(N\) es grande.

Por ejemplo

\[ \lim_{N \to \infty} \frac{1}{N} \sum_{i=1}^N X_i = \mu \]

En esta lección vimos que la cadena de markov, un proceso estocástico donde no se cumple el supuesto iid, puede tener en ciertos casos una distribución estacionaria

Nota

La distribución estacionaria \(\pi\) de una cadena de Markov con matriz de transición \(P\) es tal que \(\pi P = \pi\)

Teorema de ergodicidad: Una cadena de Markov irreducible y aperiodica tiene una distribución estacionaria \(\pi\) única, independiente de valor del estado inicial y que cumple

\[ \lim_{n\to \infty} s_j(n) = \pi_j \]

donde los componentes de \(\pi\) representan la fracción de tiempo que la cadena estará en cada uno de los estados luego de observarla por un largo tiempo

Importante

El límite de observar la cadena por un tiempo largo es análogo al análisis de estadísticos estáticos sobre muestras grandes. Esto es el equivalente a la ley de los grandes números para el caso de la cadena de Markov

5.4.1. Breves notas históricas¶

La primera ley de los grandes números: Jacob Bernoulli mostró la primera versión de la Ley de los grandes números en su Ars Conjectandi en 1713. Esta primera versión parte del supuesto de que las VAs son iid. Bernoulli era un firme creyente del destino, se oponía al libre albedrío y abogaba por el determinismo en los fenómenos aleatorios.
La segunda ley de los grandes números: En 1913 el matemático ruso Andrei Markov celebró el bicentenario de la famosa prueba de Bernoulli organizando un simposio donde presentó su nueva versión de la Ley de los grandes números que aplica sobre la clase de procesos estocásticos que hoy llamamos procesos de Markov, de esta forma extendiendo el resultado de Bernoulli a un caso que no es iid.
La pugna de Markov y Nekrasov: En aquellos tiempos Markov estaba en pugna con otro matemático ruso: Pavel Nekrasov. Nekrasov había publicado previamente que “la independencia era una condición necesaria para que se cumpla la ley de los grandes números”. Nekrasov mantenia que el comportamiento humano al no ser iid no podía estar guiado por la ley de los grandes números, es decir que los humanos actuan voluntariamente y con libre albedrío. Markov reaccionó a esta afirmación desarrollando un contra-ejemplo que terminó siendo lo que hoy conocemos como los procesos de Markov

1: La cadena de Markov anterior modela un problema conocido como la ruina del apostador, puedes estudiar de que se trata aquí

Introducción al método de Monte Carlo y a MCMC

Cadenas de Markov

Contenido

5. Cadenas de Markov¶

5.1. Matriz de transición de una cadena de Markov¶

5.1.1. Ejemplo: Predicción de clima con cadena de dos estados¶

5.2. Estado estacionario de la cadena de Markov¶

5.2.1. Generalizando el ejemplo anterior¶

5.3. Algoritmo general para simular una cadena de Markov discreta¶

5.4. Ley de los grandes números para variables no i.i.d.¶

5.4.1. Breves notas históricas¶