6. Introducción a Markov Chain Monte Carlo¶

Las cadenas de Markov tienen dos usos principales. En primer lugar las cadenas de Markov se ocupan como modelo o aproximación de fenómenos que evolucionan en el tiempo. Esto es lo que vimos la lección anterior.

En estos casos corresponde hacer la pregunta de si acaso el fenómeno que estoy estudiando cumple con la propiedad de Markov. Por ejemplo ¿Es la evolución del clima un proceso de Markov?

En segundo lugar las cadenas de Markov son un componente fundamental de una clase de algoritmos conocidos como Markov Chain Monte Carlo (MCMC). El objetivo de MCMC es crear sintéticamente una cadena de Markov que converge a una distribución en la cual estamos interesados y que no podemos simular de forma analítica y/o explícita. MCMC es considerado una revolución en computación científica y tiene aplicaciones en prácticamente todos las disciplinas.

En esta lección estudiaremos el algoritmos de Metropolis, una de las formulaciones originales de MCMC y también uno de los diez algoritmos más importantes del Siglo XX.

6.1. Monte Carlo y muestreo por importancia (IS)¶

MCMC es una poderosa herramienta para muestrear y calcular valores esperados a partir de distribuciones complejas. En este sentido es una extensión de la idea básica de Monte Carlo que vimos en las primeras lecciones.

Recordemos, con Monte Carlo podemos estimar el valor esperado de una función \(f(x)\) en base a muestras usando

\[ \mathbb{E}_{x\sim p(x)}[f(X)] \approx \frac{1}{N} \sum_{i=1}^N f(x_i) \quad x_i \sim p(x) \]

Advertencia

El estimador anterior sólo se puede usar si es posible muestrear directamente de \(p(x)\)

Si no puedo muestrear de \(p(x)\) pero si puedo evaluarla, se puede recurrir a la técnica de muestreo por importancia (IS) que se define a continuación.

Sea una distribución de propuestas o distribución de importancia \(q(x)\) de la cual es posible evaluar y además muestrear. En ese caso se puede reescribir la ecuación anterior como sigue

\[\begin{split} \begin{align} \mathbb{E}_{x\sim p(x)}[f(X)] &= \int p(x) f(x) \,dx = \int q(x) \frac{p(x)}{q(x)} f(x) \,dx \nonumber \\ &= \mathbb{E}_{x\sim q(x)}\left[ \frac{p(x)}{q(x)} f(X)\right] \nonumber \\ &\approx \frac{1}{N} \sum_{i=1}^N w_i f(x_i) \quad x_i \sim q(x) \nonumber \end{align} \end{split}\]

donde \(w_i = \frac{p(x)}{q(x)}\) se llama la ponderación de importancia.

Una distribución de importancia adecuada no sólo nos permite resolver el problema sino que tiende a presentar una varianza más baja que el estimador original de Monte Carlo. Notar que no es necesario escoger una distribución de importancia que sea igual a la distribución original, pero se debe tener en cuanta que que \(q(x)\) debe ser tal que \(p(x)=0\) cuando \(q(x)=0\)

Ejercicio

Sea una linea de teléfono de soporte tecnológico que recibe en promedio 2 llamadas por minuto ¿Cuál es la probabilidad de que ellos tengan que esperar por lo menos 10 minutos para recibir 9 llamadas?

Responda utilizando una simulación de Monte Carlo y muestreo por importancia. Utilice una distribución gamma para modelar los tiempos de espera.

Solución: Primero definimos la distribución de los tiempo de espera como se indica

b = 2. # Eventos promedio por minuto
a = 9 # Cantidad de eventos
p = scipy.stats.gamma(a, scale=1/b) 

Luego implementamos la función que queremos estimar

f = lambda x: x > 10

Para IS utilizaremos la siguiente función de propuesta

q = scipy.stats.norm(scale=10)

A continuación simulamos para Monte Carlo e IS usando número de muestras cada vez más grandes e inspeccionamos como evoluciona nuestro estimador del valor esperado de \(f(x)\)

# Simulación
mc_result, is_result = {}, {}
true_result = 1 - p.cdf(10)
for N in np.logspace(1, 4, num=100):
    # Monte carlo clasico
    x = p.rvs(size=int(N))
    mc_result[N] = np.mean(f(x))
    # Muestreo por importancia
    x = q.rvs(size=int(N))
    w = p.pdf(x)/q.pdf(x)
    is_result[N] = np.mean(w*f(x))

mc_plot = hv.Curve((list(mc_result.keys()), list(mc_result.values())), 
                   'Cantidad de muestras', 
                   'Probabilidad de recibir 10\n llamadas en 9 minutos', 
                   label='Monte Carlo').opts(logx=True)
is_plot = hv.Curve((list(is_result.keys()), list(is_result.values())), label='Importance Sampling')
true_plot = hv.HLine(true_result)
hv.Overlay([mc_plot, is_plot, true_plot])

Nota

En este caso el problema tiene solución teórica conocida (linea punteada). El estimador basado en IS converge más rápido y con menos varianza que el estimador basado en Monte Carlo convencional

6.1.1. Limitaciones de IS¶

Las técnicas de muestreo por importancia (y muestreo por rechazo) permiten calcular valores esperados de distribuciones que puedo evaluar pero no muestrear. También vimos que favorece en la disminución de la varianza del estimador.

Pero existen casos más complicados donde no es fácil utilizar IS

Casos en que no es posible muestrear y tampoco evaluar la distribución de interés
Casos en que el espacio tiene una dimensionalidad demasiado alta

Digamos que estamos interesados en la distribución de una variable \(\theta\) condicionada a un conjunto de observaciones \(D\), esto corresponde al posterior \(p(\theta|D)\). Sólo en contadas ocasiones este posterior corresponderá a una distribución teórica conocida.

Más en general tendremos

\[ p(\theta|D) = \frac{p(D|\theta) p(\theta)}{p(D)} \]

donde \(p(D|\theta)\) es la verosimilitud, \(p(\theta)\) es el prior y

\[ p(D) = \int_\theta p(D, \theta) \,d\theta \]

es la evidencia o verosimilitud marginal que no depende de \(\theta\).

Advertencia

Si la dimensionalidad de \(\theta\) es grande la integral será muy difícil o derechamente imposible de calcular analíticamente. Si no podemos al menos evaluar \(p(\theta|D)\) no podemos usar IS

Otro problema de los espacios de alta dimensionalidad es que recorrer ese espacio completo de forma independiente puede ser muy lento o de plano infactible

Consejo

MCMC puede usarse aun cuando existan las dos dificultades anteriormente mencionadas

6.2. Intuición de MCMC¶

En MCMC en lugar de muestrear de manera i.i.d., utilizamos una cadena de Markov que corresponde a la secuencia de pasos que damos en el espacio de alta dimensionalidad.

En la siguiente figura la distribución de interés se muestra de color rojo. En la subfigura de la izquierda usamos una distribución de importancia simple (contorno verde). Muchos de los puntos tendrán un ponderador de importancia cercano a cero.

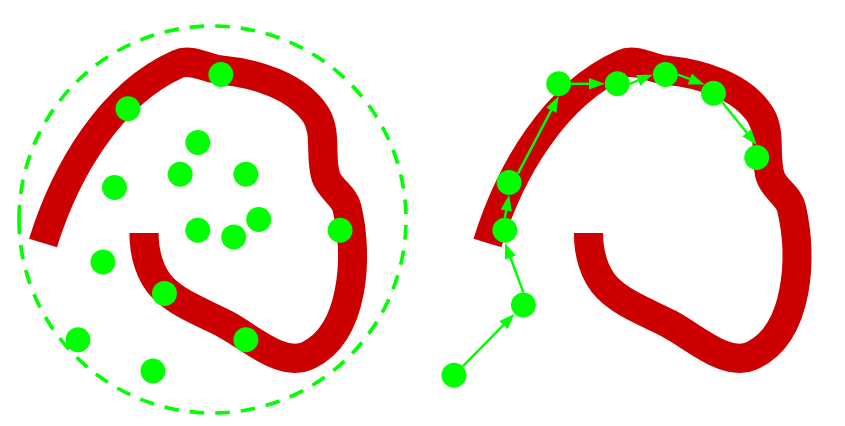
Los métodos de MCMC se basan en “diseñar” una cadena de Markov tal que converja a la distribución complicada que nos interesa, como muestra la subfigura de la derecha.

Luego sólo tenemos que dejar que la cadena corra “por un tiempo largo” para que la convergencia se cumpla y finalmente usar los valores de los estados de la cadena como una representación de la distribución a la cual no tenemos acceso.

Glosario MCMC:

La secuencia de valores de los estados de la cadena se llama trace (traza)
El tiempo que demora en converger la cadena se llama mixing time (tiempo de mezcla)
Es común eliminar de la trasa los primeros estados de la cadena pues no están cerca de la distribución de interés. Esto se denomina burn-in (quema).

¿Qué es diseñar una cadena de Markov?

Extendiendo al caso de un estado continuo en lugar de discreto, la distribución estacionaria \(\pi\) debe cumplir

\[ \int \pi(\theta_t) q(\theta_{t+1}|\theta_t) \,d\theta_t = \pi (\theta_{t+1}) \]

Luego diseñar la cadena de Markov consiste en encontrar las probabilidades de transición \(q(\theta_{t+1}|\theta_t)\) dado que conozco \(\pi\).

Nota

Esto es “al reves” de lo que hicimos en la lección pasada, que era encontrar \(\pi\) dado que conozco la matriz de transición

A continuación veremos veremos que no necesitamos conocer “completamente” \(\pi\) para lograr esto, basta conocerlo hasta una constante.

6.3. Algoritmo de Metropolis¶

El algoritmo de Metropolis fue el primer algoritmo de tipo MCMC. Fue propuesto por Nicholas Metropolis, colega de Ulam y Von Neumann, en el año 1953 para entender la transición de fase que experimetan los materiales. El paper original sentó las bases de lo que hoy conocemos como el algoritmo de Metropolis y el algoritmo de Simulated Annealing (SA)

El algoritmo de Metropolis utiliza un random walk para definir las probabilidades de transición de la cadena. Sea

\[ \theta_{t+1} = \theta_{t} + \epsilon \]

donde \(\epsilon\) tiene una distribución centrada en cero y simétrica, típicamente una gaussiana

\[ \epsilon \sim \mathcal{N}(0, I\sigma_\epsilon^2), \]

donde \(\sigma_\epsilon\) es hiper parámetro del algoritmo. Por definición tenemos entonces que

\[ \theta^* \sim q(\theta_{t+1}|\theta_{t}) = \mathcal{N}(\theta_{t}, I \sigma_\epsilon^2) \]

donde \(q\) se denomina distribución de propuestas y su objetivo es proponer un valor para \(\theta_{t+1}\).

Luego el nuevo valor de \(\theta\) se acepta con una tasa definida como

\[ \alpha(\theta^*|\theta_{t}) = \min(1, r) \]

donde

\[ r = \frac{ p(\theta^*)q(\theta_{t}|\theta^*) }{ p(\theta_t)q(\theta^*|\theta_{t})} = \frac{p(\theta^*)}{p(\theta_t)} \]

donde la última equivalencia se tiene por la simetría

Entonces

Si \(\theta^*\) es mucho mejor que \(\theta_t\) entonces se acepta
Si \(\theta^*\) es mucho peor que \(\theta_t\) entonces se rechaza
En caso de duda se deja al azar

Respecto de \(\sigma_\epsilon\)

Si su valor es grande tendremos muchos rechazos
Si su valor es pequeño la difusión será lenta y podrían requerirse muchas iteraciones

Juntando lo anterior se tiene que el algoritmo completo es

Algorithm (Algoritmo de Metropolis)

Entradas Dado el largo de la cadena \(N\) y una distribución de propuestas \(q()\)

Salidas Una traza \(\theta_t\) con \(t=0,\ldots, N\)

Escoger un valor inicial \(\theta_0\)
Para \(n=1,2,\ldots, N\)
1. Muestrear \(\theta^* \sim q(\theta_{t+1}|\theta_{t})\)
2. Muestrear \(u \sim U[0, 1]\)
3. Si
\[ u < \alpha(\theta^*|\theta_{t}) \]

entonces

\[ \theta_{t+1} = \theta^* \]

de lo contrario

\[ \theta_{t+1} = \theta_{t} \]

A continuación se muestra una implementación en Python de este algoritmo.

Se utiliza una normal como distribución de propuestas
Se precalculan los valores de la distribución de propuesta de la variable U para mayor eficiencia
El argumento p es una función de Python con una variable (theta)
El argumento mix_time define el largo de la traza resultante
El argumento sigma_eps es la desviación estándar de la distribución de propuestas

def metropolis(p, mix_time, sigma_eps=1.): 
    trace_theta = np.zeros(shape=(mix_time, )) # Retorna la traza de theta
    trace_theta[0] = np.random.randn() # Theta inicial
    qs = scipy.stats.norm(loc=0, scale=sigma_eps).rvs(size=mix_time)
    us = scipy.stats.uniform.rvs(size=mix_time)
    for n in range(1, mix_time):
        theta_star = trace_theta[n-1] + qs[n] # Theta propuesto
        r = p(theta_star)/p(trace_theta[n-1])
        alpha = np.amin([1., r])
        if us[n] < alpha: 
            trace_theta[n] = theta_star
        else:
            trace_theta[n] = trace_theta[n-1]
    return trace_theta

6.3.1. Algoritmo de Metropolis-Hastings¶

El algoritmo de Metropolis-Hastings es una generalización del algoritmo de Metropolis para el caso donde la distribución de propuestas ya no es simétrica por lo que \(r\) es ahora

\[ r = \frac{ p(\theta^*)q(\theta_{t}|\theta^*) }{ p(\theta_t)q(\theta^*|\theta_{t})} \]

El algoritmo procede de forma idéntica al caso anterior

6.4. MCMC para estimar posteriors¶

Si estamos interesados en un posterior \(p(\theta_t|\mathcal{D})\) cuya evidencia \(p(\mathcal{D})\) es difícil o imposible de calcular, podemos usar el algoritmo de Metropolis sin problema pues

\[ r = \frac{p(\theta^*|\mathcal{D})}{p(\theta_t|\mathcal{D})} = \frac{p(\mathcal{D}|\theta^*)p(\theta^*)}{p(\mathcal{D}|\theta_t)p(\theta_t)} \frac{p(\mathcal{D})}{p(\mathcal{D})} = \frac{p(\mathcal{D}|\theta^*)p(\theta^*)}{p(\mathcal{D}|\theta_t)p(\theta_t)} \]

Es decir que basta con conocer la verosimilitud y el prior. Pongamos en práctica esto con un ejemplo

Ejercicio

Sea un conjunto de muestras con \(N=5\)

\[ \mathcal{D} = \{ 9.37, 10.18, 9.16, 11.60, 10.33 \} \]

que corresponden a realizaciones i.i.d

\[ X_1, X_2, \ldots, X_5|\theta \sim \mathcal{N}(\theta, \sigma^2=1) \]

donde

\[ \theta \sim \mathcal{N}(\mu=5, \tau^2=10) \]

Dada la verosimilitud y el prior anteriores simule el posterior \(p(\theta|\mathcal{D})\) utilizando el algoritmo de Metropolis.

Solución: Primero implementamos la verosimilitud y el prior

prior = lambda theta : scipy.stats.norm(loc=5, scale=np.sqrt(10)).pdf(theta)
likelihood = lambda theta, data : np.prod([scipy.stats.norm(loc=theta, scale=1).pdf(x) for x in data])
p = lambda theta, data: likelihood(theta, data)*prior(theta)

Luego obtenemos una traza entregandole p a la función metropolis que implementamos anteriormente. Se queman (descartan) las primeras 100 muestras de la traza

from functools import partial

D = np.array([9.37, 10.18, 9.16, 11.60, 10.33])
burn_in = 100
theta_trace = metropolis(partial(p, data=D), mix_time=5000)[burn_in:]
edges, bins = np.histogram(theta_trace, bins=20, density=True)

La siguiente figura muestra la evolución de la traza (izquierda) y la densidad estimada a partir de la traza (derecha).

tn2 = (len(D)/1. + 1./10)**(-1)
wn = tn2/10.
theta_plot = np.linspace(np.amin(theta_trace), np.amax(theta_trace), num=100)
theorical_dist = scipy.stats.norm(loc=np.mean(D)*(1-wn)+5*wn, 
                                  scale=np.sqrt(tn2)).pdf(theta_plot)

p_trace = hv.Curve((theta_trace), 'Step', 'Theta')
p_true = hv.HLine(np.mean(D)*(1-wn) + 5*wn)
p_dist = hv.Histogram((edges, bins), kdims='Theta', label='MCMC').opts(xlim=(8, 12), alpha=0.75, width=250)
p_dist_true = hv.Curve((theta_plot, theorical_dist), 
                       label='Teórica').opts(color='k', line_dash='dashed')
((p_trace * p_true) << (p_dist * p_dist_true)).opts(hv.opts.Overlay(legend_position='top'))

Nota

En este caso (muy particular) el posterior se puede calcular analíticamente como

\[ p(\theta|\mathcal{D}) = \mathcal{N}\left ( \bar x (1- w_N) + \mu w_N , \tau_N^2 \right) \]

donde \(w_N = \tau_N^2/\tau^2\) y \(\tau_N^2 = (N/\sigma^2 + 1/\tau^2)^{-1}\)

El posterior analítico se muestra con linea negra punteada en la figura anterior. La solución de MCMC estima con bastante fidelidad la distribución teórica.

Advertencia

Pero, ¿Qué pasa en el caso general donde hay un posterior análitco para comparar? ¿Cómo puedo comprobar si la cadena convergió a su estado estacionario y que el posterior obtenido es válido?

En la próxima lección veremos algunas técnicas para diagnosticar la convergencia de la cadena y también veremos en mayor detalle la influencia de los hiperparámetros del algoritmo de metrópolis

Introducción al método de Monte Carlo y a MCMC

Introducción a Markov Chain Monte Carlo

Contenido

6. Introducción a Markov Chain Monte Carlo¶

6.1. Monte Carlo y muestreo por importancia (IS)¶

6.1.1. Limitaciones de IS¶

6.2. Intuición de MCMC¶

6.3. Algoritmo de Metropolis¶

6.3.1. Algoritmo de Metropolis-Hastings¶

6.4. MCMC para estimar posteriors¶