Programación probabilística
Contenido
8. Programación probabilística¶
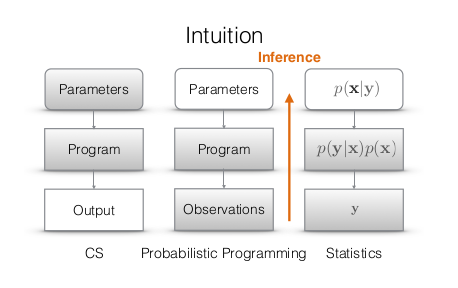
La programación probabilística (PP) es un nuevo paradigma que busca combinar los lenguajes de programación de propósito general con el modelamiento probabilístico.
El objetivo es hacer estadística y en particular inferencia Bayesiana usando las herramientas de ciencias de la computación. Como muestra el siguiente diagrama la PP corre en dos direcciones:
El lenguaje Python tiene un ecosistema rico en frameworks y librerías de PP:
En este tutorial aprenderemos a usar la librería NumPyro para:
Definir un modelo bayesiano en base a una verosimilitud y a un prior
Aplicar distintos algoritmos de MCMC sobre el modelo
Verificar la convergencia y analizar los posteriors
A grandes rasgos NumPyro opera como una especie de interfaz entre la librería NumPy de computo numérico y el backed pyro de programación probabilística. Entre sus ventajas se encuentra el uso de JAX para hacer compilación just in time en CPU/GPU, lo cual la hace muy eficiente.
Como ejemplo para aprender a usar esta librería utilizaremos un modelo de regresión lineal Bayesiana.
import numpy as np
from jax import random
from jax import numpy as jnp
import numpyro
import numpyro.distributions as dists
import holoviews as hv
hv.extension('bokeh')
hv.opts.defaults(hv.opts.Curve(width=500),
hv.opts.Scatter(width=500, size=10),
hv.opts.HLine(alpha=0.5, color='k', line_dash='dashed'),
hv.opts.VLine(alpha=0.5, color='k', line_dash='dashed'))
numpyro.set_host_device_count(2)
print(f"Numpyro version: {numpyro.__version__}")
Numpyro version: 0.10.1
8.1. Formulación bayesiana de la regresión lineal¶
Consideramos que tenemos \(N\) tuplas \((x_i, y_i)\) donde \(X\) es la variable independiente e \(Y\) la dependiente.
En una regresión queremos estimar \(\mathbb{E}[Y|X]\) en base a un modelo paramétrico \(Y = f_\theta(X)\). En este caso asumiremos un modelo lineal:
donde queremos aprender los parámetros \(\theta=(w, b)\) bajo el supuesto de que \(p(\epsilon) = \mathcal{N}(0, \sigma_\epsilon^2)\), luego
y por lo tanto la verosimilitud sería:
A diferencia de una regresión “convencional” asumiremos que \(w\), \(b\) y \(\sigma_\epsilon\) no son variables determinísticas sino aleatorias y por ende tienen distribuciones. Llamamos prior a la distribución de los parámetros previo a observar nuestros datos.
En este caso particular asumiremos una distribución normal para los priors de \(w\) y \(b\):
Lo que buscamos es el posterior de los parámetros \(\theta\), es decir su distribución condicionado a nuestras observaciones \(D\) que se obtiene con el teorema de Bayes como:
y que en este caso particular es:
donde por simplicidad se asume que \(p(w,b,\sigma_\epsilon) = p(w)p(b)p(\sigma_\epsilon)\), es decir que el prior no tiene correlaciones entre los parámetros.
Importante
Estimaremos este posterior en base a muestras utilizando MCMC.
A continuación se generan los datos que utilizaremos a lo largo de este tutorial
np.random.seed(1234)
b_star, w_star, s_eps_star, N = 10, 2.5, 1., 10
x = np.random.randn(N)
y = b_star + w_star*x + np.random.randn(N)*s_eps_star
x_test = np.linspace(-3, 3, 100)
hv.Scatter((x, y)).opts(color='k')
8.2. Especificación del modelo generativo¶
El modelo generativo es aquel que “produjo” los datos. Usualmente comienza con los hiperparámetros, continua en las variables latentes (priors) y termina en las variables observadas (verosimilitud). A continuación se muestra el diagrama de placas de la regresión lineal bayesiana con todas sus variables, parámetros e hiperparámetros:
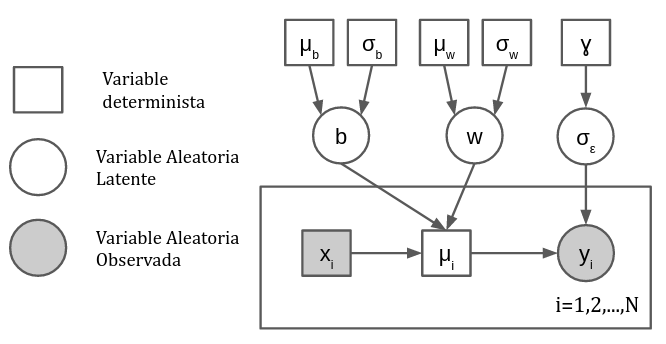
En NumPyro un modelo generativo es simplemente una función que define y relaciona las variables determinísticas y aleatorias que utilizaremos. Para crear una variable aleatoria se utiliza la primitiva:
numpyro.sample(name, # El nombre de la variable (string)
fn, # La distribución de la variable
obs, # (Opcional) Los datos observados asociados a esta variable
rng_key, # Una semilla aleatoria
...
)
Los priors son variables aleatorias que no usan el argumento obs. En cambio, para escribir la verosimilitud, utilizamos el argumento obs para proporcionar los datos. Las distribuciones conocidas se pueden importar desde numpyro.distributions.
Para definir una variable determínistica se utiliza la primitiva:
numpyro.deterministic(name, # El nombre de la variable (string)
value, # Transformación sobre otras variables del modelo
)
A continuación se muestra la implementación del modelo de regresión lineal en pyro. Utilizaremos:
una distribución normal con \(\mu_w = \mu_b = 0\) y \(\sigma_w = \sigma_b = 5.0\) para \(w\) y \(b\).
una distribución “Media”-Cauchy con \(\gamma = 5.0\) para \(\sigma_\epsilon\).
Una verosimiliud normal.
def model(x, y=None):
prior_dist = dists.Normal(loc=jnp.zeros(2), scale=5*jnp.ones(2))
theta = numpyro.sample("theta", prior_dist.to_event(1))
s_eps = numpyro.sample("s", dists.HalfCauchy(scale=5.0))
with numpyro.plate('datos', size=len(x)):
f = numpyro.deterministic('f', value=x*theta[1] + theta[0])
numpyro.sample("y", dists.Normal(loc=f, scale=s_eps), obs=y)
return f
Durante la definición del modelo también utilizamos la primitiva
numpyro.plate(name, # El nombre del contexto (string)
size=None, # El tamaño del dataset (int)
subsample_size=None, # El tamaño del minibatch (opcional)
...
)
para crear una variable y que está condicionada al conjunto de variables x. Internamente numpyro.plate también se hace cargo de paralelizar operaciones.
Si quisieramos utilizar el modelo generativo, es decir evaluarlo, debemos proporcionar una semilla aleatoria. Podemos hacer esto con numpyro.handlers.seed como se muestra a continuación
for i in range(3): # Tres semillas
seeded_model = numpyro.handlers.seed(model, random.PRNGKey(i))
print(i, seeded_model(x))
WARNING:jax._src.lib.xla_bridge:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
0 [-0.27633387 4.1023145 -2.8082418 1.7888845 2.8633554 -1.3713253
-1.2986963 2.6419346 0.9240432 6.8724265 ]
1 [-4.6081133 -2.5978503 -5.7705274 -3.6599596 -3.1666636 -5.1108303
-5.077486 -3.2683191 -4.0570135 -1.3260756]
2 [-1.6500422 0.9005755 -3.1249104 -0.4470265 0.17886627 -2.2878885
-2.2455812 0.04988593 -0.95080745 2.5142007 ]
Con seeded_model podemos inspeccionar la especificación del modelo con numpyro.handlers.trace como se muestra a continuación. También podemos obtener un diagrama de placas con numpyro.render_model.
exec_trace = numpyro.handlers.trace(seeded_model).get_trace(x)
print(numpyro.util.format_shapes(exec_trace))
#numpyro.render_model(model, (x, y)) # Requiere instalar graphviz
Trace Shapes:
Param Sites:
Sample Sites:
theta dist | 2
value | 2
s dist |
value |
datos plate 10 |
y dist 10 |
value 10 |
Una forma más completa para obtener las muestras generadas por el modelo es utilizando:
numpyro.infer.Predictive(model, # El modelo que definimos anteriormente
num_samples=None, # El número de muestras que deseamos generar
return_sites=(), # Las variables de las cuales deseamos muestrear
posterior_samples=None, # Opcional: Lo veremos más adelante
...
)
lo cual crea un objeto que podemos utilizar para evaluar nuestro modelo y recuperar las muestras de todas sus variables aleatorias y determinísticas. Más adelante veremos como utilizar este objeto para obtener muestras del posterior de nuestro modelo.
# Creamos el objetivo Predictive
predictive = numpyro.infer.Predictive(model,
num_samples=2000)
# Para muestrear el objeto predictive requiere una semilla aleatoria y las variables de entrada del modelo
rng_key = random.PRNGKey(12345)
rng_key, rng_key_ = random.split(rng_key)
prior_samples = predictive(rng_key_, x_test)
prior_samples.keys()
dict_keys(['f', 's', 'theta', 'y'])
En base a las muestras podemos construir histogramas o gráficos de densidad como se muestra a continuación.
joint = hv.Bivariate((prior_samples['theta'][:, 1], prior_samples['theta'][:, 0]),
kdims=['w', 'b']).opts(cmap='Blues', line_width=0, filled=True)
wmarginal, bmarginal = ((hv.Distribution(joint, kdims=[dim])) for dim in 'wb')
(joint) << bmarginal.opts(width=125) << wmarginal.opts(height=125)
La distribuciones estimadas a partir de las muestras son consistentes con los priors que escogimos.
Adicionalmente podemos estudiar el espacio de posibles modelos:
p5, p50, p95 = np.quantile(prior_samples['f'], (0.05, 0.5, 0.95), axis=0)
data = hv.Scatter((x, y), label='datos').opts(color='k')
p = []
for curve in prior_samples['f'][:100, :]:
p.append(hv.Curve((x_test, curve)).opts(color='#30a2da', alpha=0.1))
line = hv.Curve((x_test, p50), label='mediana')
shade = hv.Spread((x_test, p50, p95-p5), label='95% CI').opts(color='#30a2da', alpha=0.5)
hv.Layout([hv.Overlay(p) * data,
hv.Overlay([line, shade, data]).opts(legend_position='bottom_right')]).opts(hv.opts.Curve(width=350))
Esto se conoce como distribución prior predictiva.
Importante
Estudiar las muestras nos permite detectar tempranamente si cometimos un error en la definición del modelo.
8.3. Obteniendo muestras del posterior con MCMC¶
La maquinaria de MCMC en numpyro se accede usando la función
numpyro.infer.MCMC(sampler, # Un algoritmo muestreador, por ejemplo Metropolis
num_warmup, # Cantidad de muestras iniciales a descartar
num_samples, # Largo de la traza (sin contar burn-in)
num_chains=1, # Número de cadenas
thinning=1, # Cuantas muestras por medio de la traza se preservan
...
)
Los principales métodos de infer.MCMC son
run(): Realiza los cálculos para poblar las cadenas, espera una semilla aleatoria y los mismos argumentos que la funciónmodelprint_summary(): Retorna una tabla con los momentos estadísticos de los parámetros y algunos diagnósticosget_sample(): Retorna la traza, es decir las muestras del posterior
El argumento más importante de infer.MCMC es el sampler. Entre los algoritmos disponibles se encuentran: HMC (Hamiltonian Monte Carlo) y NUTS (No-U turn sampler). Ambos son muestreadores para parámetros continuos que utilizan información del gradiente para proponer transiciones.
Cada iteración de HMC/NUTS es más costosa con respecto a Metropolis-Hastings, pero en general se requieren menos iteraciones ya que converge más rápido al estado estacionario.
Ver también
Recomiendo revisar los siguientes ejemplos animados para tener una idea conceptual de la diferencia entre Metropolis y HMC.
NUTS es ampliamente considerado como el estado del arte en algoritmos de propuestas para paramétros continuos. Veamos a continuación como se muestrea usando MCMC y NUTS con numpyro.
rng_key, rng_key_ = random.split(rng_key)
sampler = numpyro.infer.MCMC(sampler=numpyro.infer.NUTS(model),
num_samples=1000, num_warmup=100, thinning=1,
num_chains=2, jit_model_args=True)
sampler.run(rng_key_, x, y)
Antes de usar el posterior es muy recomendable diagnosticar la adecuada convergencia de las cadenas. En primer lugar podemos utilizar:
sampler.print_summary(prob=0.9)
mean std median 5.0% 95.0% n_eff r_hat
s 1.24 0.37 1.17 0.71 1.76 484.24 1.00
theta[0] 10.14 0.40 10.14 9.52 10.79 2334.20 1.00
theta[1] 2.97 0.38 2.97 2.37 3.59 806.48 1.00
Number of divergences: 0
De donde podemos resaltar que
El estadísitco de Gelman Rubin es cercano a 1 para todos los parámetros
El número de muestras efectivo es alto
No hubieron divergencias durante el muestro
Todo indicativos de una buena convergencia. También podemos obtener las trazas utilizando:
posterior_samples = sampler.get_samples()
posterior_samples.keys()
dict_keys(['f', 's', 'theta'])
A continuación se visualizan las trazas de w, b y s:
p1 = hv.Curve((posterior_samples['theta'][:, 1]), 'Iteraciones', 'Traza', label='w')
p2 = hv.Curve((posterior_samples['theta'][:, 0]), 'Iteraciones', 'Traza', label='b')
p3 = hv.Curve((posterior_samples['s']), 'Iteraciones', 'Traza', label='s')
hv.Overlay([p1, p2, p3]).opts(legend_position='top')
La autocorrelación de la traza es una excelente herramienta para diagnosticar la correcta operación del algoritmo.
def autocorrelation(theta_trace):
thetas_norm = (theta_trace-np.mean(theta_trace))/np.std(theta_trace)
rho = np.correlate(thetas_norm,
thetas_norm, mode='full')
return rho[len(rho) // 2:]/len(theta_trace)
rho = {}
rho['s'] = autocorrelation(posterior_samples['s'])
rho['w'] = autocorrelation(posterior_samples['theta'][:, 1])
rho['b'] = autocorrelation(posterior_samples['theta'][:, 0])
En este caso la autocorrelación de las trazas es:
p = []
for key, value in rho.items():
p.append(hv.Curve((value), 'Retardo', 'Traza', label=key).opts(alpha=0.5))
hv.Overlay(p)
Nota
Para todos los parametros la autocorrelación decrece rápidamente y se mantiene en torno a cero.
Las métricas y diagnósticos nos indican que el algoritmo MCMC convergió al estado estacionario. Por lo tanto podemos inspeccionar y utilizar el posterior para nuestro modelo de regresión lineal sin preocupaciones.
A continuación se muestran los posterior de w y b en base a estimadores de densidad construidos con las muestras de la traza:
w_posterior = posterior_samples['theta'][:, 1]
b_posterior = posterior_samples['theta'][:, 0]
joint = hv.Bivariate((w_posterior, b_posterior), kdims=['w', 'b']).opts(cmap='Blues', line_width=0, filled=True)
wmarginal, bmarginal = ((hv.Distribution(joint, kdims=[dim])) for dim in 'wb')
(joint) << bmarginal.opts(width=125) * hv.VLine(b_star) << wmarginal.opts(height=125) * hv.VLine(w_star)
Nota
Claramente el posterior \(p(\theta| \mathcal{D})\) se ha desplazado con respecto al prior \(p(\theta)\) que vimos anteriormente. Además está muy cercano a los valores “reales” que generaron los datos (linea punteada negra).
8.4. Realizando predicciones con el posterior¶
Ahora que tenemos el posterior de los parámetros podemos usarlo para calcular la distribución posterior predictiva en función de nuevos datos \(\textbf{x}\):
donde en este caso \(\theta = (w, b, \sigma)\) y se asume que \(y\) es condicionalmente independiente de \(\mathcal{D}\) dado que conozco \(\theta\).
La parte más difícil era estimar \(p(\theta| \mathcal{D})\) el cual ya tenemos gracias a MCMC. Para obtener muestras del posterior predictivo podemos nuevamente usar la clase predictive pero ahora le entregramos las muestras del posterior como argumento.
predictive = numpyro.infer.Predictive(model,
return_sites=(["f"]),
posterior_samples=posterior_samples)
posterior_predictive_samples = predictive(random.PRNGKey(1), x_test)
En la siguiente figura aparecen los datos como puntos negros y 100 muestras del posterior predictivo (lineas azules)
p5, p50, p95 = np.quantile(posterior_predictive_samples['f'], (0.05, 0.5, 0.95), axis=0)
data = hv.Scatter((x, y), label='datos').opts(color='k')
p = []
for curve in posterior_predictive_samples['f'][:100, :]:
p.append(hv.Curve((x_test, curve)).opts(color='#30a2da', alpha=0.1))
line = hv.Curve((x_test, p50), label='mediana')
shade = hv.Spread((x_test, p50, p95-p5), label='95% CI').opts(color='#30a2da', alpha=0.5)
hv.Layout([hv.Overlay(p) * data,
hv.Overlay([line, shade, data]).opts(legend_position='bottom_right')]).opts(hv.opts.Curve(width=350))
Importante
Nuestro modelo bayesiano nos retorna una distribución de soluciones.
Con el posterior podemos estudiar no sólo la solución más probable sino también el rango de las soluciones. El rango o ancho de la distribución está relacionado a la incertidumbre de nuestro modelo y observaciones (ruido).
Ver también
Puedes estudiar ejemplos con otros modelos probabilísticos en: https://magister-informatica-uach.github.io/INFO337/lectures/11_MCMC/lecture2.html