7. Calibración y diagnóstico en MCMC¶

En esta lección nos enfocaremos en como diagnósticar un correcto resultado de un algoritmo de tipo MCMC. Para esto revisaremos algunas métricas y criterios ampliamente usados y utilizaremos para calibrar el algoritmo de Metropolis que vimos la lección anterior.

7.1. Tiempo de mezcla (mixing time)¶

Previamente hemos visto como diseñar una cadena de Markov finita tal que converja a una distribución estacionaria \(\pi\) de nuestro interés. Pero, ¿Cuánto debemos esperar para que ocurra la convergencia?

El tiempo de mezcla para una cadena de Markov irreducible y aperiódica se define como

\[ t_{mix}(\epsilon) = \min \left(n > 0: \|s(n) - \pi\|_{TV} < \epsilon \right) \]

es decir el mínimo tiempo (número de pasos) tal que estemos a una distancia \(\epsilon\) de la distribución estacionaria \(\pi\).

De la ecuación anterior el operador

\[ \|p - q\|_{TV} = \max_{x\in\mathcal{\Omega}} \|p(x) - q(x)\| \]

se conoce como la distancia de variación total entre dos distribuciones.

Se tienen algunas garantías teóricas con respecto al tiempo de mezcla, en particular la siguiente cota superior

\[ t_{mix}(\epsilon) < \log \left(\frac{1}{\epsilon \sqrt{\min_j \pi_j}} \right) \frac{1}{1-\lambda_*} \]

donde \(\lambda_*\) es el segundo valor propio más grande de la matriz de transición \(P\) de la cadena.

La descomposición en valores propios de la matriz de transición de una cadena irreducible y de \(\mathcal{S}\) estados se puede escribir como

\[ P^n = \sum_{i=1}^\mathcal{S} \alpha_i \lambda_i^n = \pi + \sum_{i=2}^\mathcal{S} \alpha_i \lambda_i^n \]

La última igualdad corresponda a una propiedad de la cadena de Markov irreducible: Su valor propio más grande siempre es igual a uno y su vector propio asociado es la distribución estacionaria.

Importante

Todos los demás valores propios se harán eventualmente cero cuando \(n \to \infty\), siendo el segundo valor propio más grande y distinto de uno el que más se demore

7.2. Autocorrelación en la cadena y número de muestras efectivo¶

Como vimos en la lección anterior el algoritmo MCMC converge asintóticamente a la distribución estacionaria. Pero en la práctica no podemos esperar hasta \(n\to \infty\)

¿Cómo podemos confirmar si nuestro algoritmo MCMC ha convergido?

Por construcción, las muestras de nuestra traza son dependientes, pues \(\theta_{t+1}\) se calcula a partir de \(\theta_t\).

Sin embargo, luego de un periódo de burn-in, las probabilidades de transición de la cadena debería converger a la distribución estacionaria y volverse independientes del tiempo

Es decir que podemos confirmar la convergencia estudiando la autocorrelación de la traza

\[ \rho(\tau) = \mathbb{E}\left[(\theta_t - \bar \theta)(\theta_{t+\tau} - \bar \theta)\right] \]

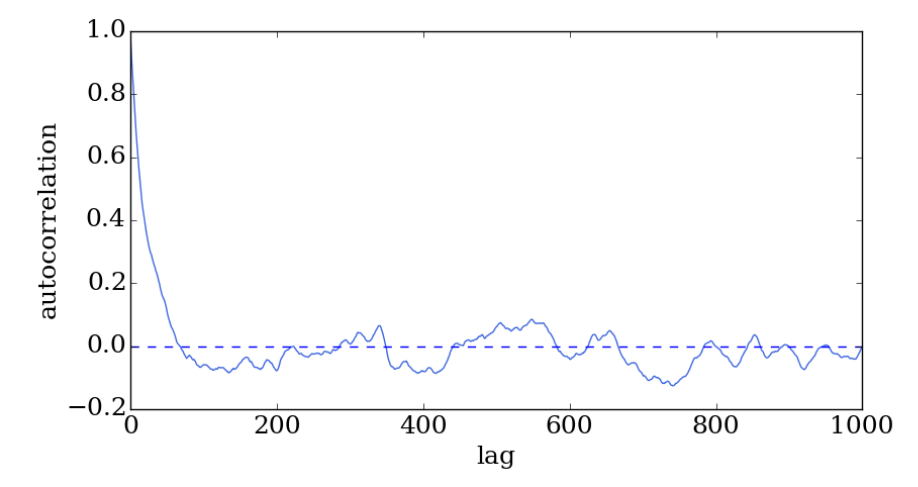
La autocorrelación nos indica que tanto las muestras de una serie de tiempo dependen de muestras pasadas.

En este caso, al graficar \(\rho\) en función de \(\tau\) buscamos una autocorrelación que converja rapidamente y que luego fluctue en torno a cero

7.3. Calibrando MCMC en base a la autocorrelación de la traza¶

En la lección pasada vimos que el algoritmo de Metropolis tiene un hiperparámetro \(\sigma_\epsilon\) que corresponde a la desviación estándar de la distribución de propuestas.

Nota

Este hiperparámetro repercute fuertemente en la convergencia del algoritmo de Metropolis.

Para estudiar la convergencia utilizaremos la función de autocorrelación. A continuación se muestra una implementación de la función de autocorrelación en base a np.correlate

def autocorrelation(theta_trace):
    thetas_norm = (theta_trace-np.mean(theta_trace))/np.std(theta_trace)
    rho = np.correlate(thetas_norm, 
                       thetas_norm, mode='full')
    return rho[len(rho) // 2:]/len(theta_trace)

Consideremos el ejemplo mostrado en la lección anterior y estudiamos como cambia la autocorrelación de las trazas para distintos valores de sigma_eps

def metropolis(p, mix_time, sigma_eps=1., random_seed=None):
    if random_seed is not None:
        np.random.seed(random_seed)
    trace_theta = np.zeros(shape=(mix_time, )) # Retorna la traza de theta
    trace_theta[0] = np.random.randn() # Theta inicial
    qs = scipy.stats.norm(loc=0, scale=sigma_eps).rvs(size=mix_time)
    us = scipy.stats.uniform.rvs(size=mix_time)
    ar = 0
    for n in range(1, mix_time):
        theta_star = trace_theta[n-1] + qs[n] # Theta propuesto
        r = p(theta_star)/p(trace_theta[n-1])
        alpha = np.amin([1., r])
        if us[n] < alpha: 
            trace_theta[n] = theta_star
            ar += 1
        else:
            trace_theta[n] = trace_theta[n-1]
    return trace_theta, float(ar)/mix_time

D = np.array([9.37, 10.18, 9.16, 11.60, 10.33])
prior = lambda theta : scipy.stats.norm(loc=5, scale=np.sqrt(10)).pdf(theta)
likelihood = lambda theta, data : np.prod([scipy.stats.norm(loc=theta, scale=1).pdf(x) for x in data])
p = lambda theta, data: likelihood(theta, data)*prior(theta)

from functools import partial

np.random.seed(12345)

traces = {}
for sigma in [0.1, 1., 2., 10.]:
    trace, ar = metropolis(partial(p, data=D), mix_time=2000, sigma_eps=sigma)
    traces[sigma] = (trace, autocorrelation(trace))
    print(f"Fracción de aceptación: {ar:0.4f}")

Fracción de aceptación: 0.8985
Fracción de aceptación: 0.4630
Fracción de aceptación: 0.2610
Fracción de aceptación: 0.0575

trace_plots = []
for sigma, (trace, rho) in traces.items():
    trace_plots.append(hv.Curve((trace), 'Pasos', 'Traza', label=f'sigma_eps={sigma}'))
    trace_plots.append(hv.Curve((rho), 'Pasos', 'Autocorrelación', label=f'sigma_eps={sigma}'))
hv.Layout(trace_plots).cols(2).opts(hv.opts.Curve(width=300, height=200))

De la figura podemos ver que

Si sigma_eps es pequeño todos las propuestas son aceptadas, pero la correlación entre ellas es alta porque son poco diversas
Si sigma_eps es grande ocurren demasiadas propuestas malas que terminan siendo rechazadas. Esto hace que las propuestas buenas se mantengan inalteradas por largos periódos lo que se traduce en un incremento en la correlación

Una figura de mérito muy utilizada que se basa en la función de autocorrelación es el número de muestras efectivas o effective sample size (ESS)

\[ n_{eff} = \frac{N}{1 + 2 \sum_{\tau=1}^T \rho(\tau)} \]

donde \(N\) es la cantidad de muestras de la cadena y \(T\) es el instante en que la autocorrelación se vuelve por primera vez negativa

Idealmente quisieramos que \(n_{eff} = N\), pero debido a que las muestras no son independientes en realidad tendremos \(n_{eff} < N\)

Podemos calibrar nuestro algoritmo MCMC tal que maximicemos \(n_{eff}\)

def neff(rho):
    T = np.where(rho < 0.)[0][0]
    return len(rho)/(1 + 2*np.sum(rho[:T]))

for sigma, (trace, rho) in traces.items():
    print(f"Para {sigma}, el número de muestras efectivo es {neff(rho):0.4f}")

Para 0.1, el número de muestras efectivo es 8.7771
Para 1.0, el número de muestras efectivo es 105.8934
Para 2.0, el número de muestras efectivo es 291.6672
Para 10.0, el número de muestras efectivo es 89.4863

En este caso sigma_eps=2.0 alcanza el número máximo de muestras.

Otra figura de mérito muy similar a n_eff es la fracción de aceptación. La fracción de aceptación es la cantidad de propuestas aceptadas dividido las propuestas totales. La sugerencia de los expertos es calibrar el algoritmo de Metropolis tal que alcance una fracción de aceptación cercana a 23.4%

Si observamos la función metropolis veremos que la variable ar se utiliza para calcular la fracción de aceptación. Nuevamente es sigma_eps=2.0 el que está más cercano a la fracción de aceptación óptima.

7.4. Estadístico Gelman-Rubin¶

Otra forma de estudiar la convergencia es utilizando el estadístico Gelman Rubin, también conocido como \(\hat r\). Para ocuparlo se deben entrenar al menos dos cadenas (de igual largo) para cada configuración de hiperparámetros.

El estadístico

\[ \hat r = \frac{N-1}{N} + \frac{1}{N} \frac{B}{W} \]

donde \(N\) es el largo de las cadenas, \(B\) es la varianza entre las distintas cadenas y \(W\) es el promedio de las varianzas de cada cadena.

Notar que el estadístico converge al valor \(1\) si \(N\to \infty\) o \(B\to 0\), es decir si las cadenas son lo suficientemente largas o si las cadenas llegan todos al mismo valor (varianza baja entre ellas)

A continuación se muestra una implementación en Python de este estadístico

def gelman_rubin(traces):
    J = len(traces) # Cantidad de trazas
    N = len(traces[0]) # Largo de las trazas
    chain_mean = np.zeros(shape=(J, ))
    chain_var = np.zeros(shape=(J, ))
    for i, trace in enumerate(traces):
        chain_mean[i] = np.mean(trace)
        chain_var[i] = np.sum((trace - chain_mean[i])**2)/(N-1)
    total_mean = np.mean(np.concatenate(traces))    
    B = np.sum((chain_mean - total_mean)**2)*N/(J-1)
    W = np.mean(chain_var)
    return (N-1)/N + B/(W*N)

Podemos usar este estadístico para monitorear la convergencia de las cadenas. La gráfica siguiente muestra la evolución del estadístico para tres cadenas

traces = []
for i in range(3):
    trace, ar = metropolis(partial(p, data=D), mix_time=100, sigma_eps=2.0)
    traces.append(trace)

rhat = []
for i in range(2, 100):
    short_traces = [trace[:i] for trace in traces]
    rhat.append(gelman_rubin(short_traces))

trace_plot = []
for k, trace in enumerate(traces):
    trace_plot.append(hv.Curve((trace), 'Pasos', 'Traza', label=f'Traza {k+1}'))
              
gr_plot = hv.Curve((range(2,100), rhat), 'Pasos', 'Gelman Rubin')
hv.Layout([hv.Overlay(trace_plot), 
           gr_plot * hv.HLine(1)]).cols(2).opts(hv.opts.Curve(width=330, height=300), 
                                                hv.opts.Overlay(legend_position='top'))

7.5. Thinning (adelgazamiento)¶

El “adelgazamiento” es una técnica para disminuir la autocorrelación de la traza. Consiste en submuestrear la traza, reteniendo sólo cada \(t\) muestras, donde \(t\) es el “intervalo de adelgazamiento”. La idea es escoger este intervalo estudiando la función de autocorrelación

Debido a la gran cantidad de muestras que se podrían descartar es preferible ajustar adecuadamente el paso de las propuestas por sobre esta técnica

7.6. Material extra¶

La siguiente es una lista de artículos complementarios si desean profundizar en algunos de los tópicos de esta lección

Introducción al método de Monte Carlo y a MCMC

Calibración y diagnóstico en MCMC

Contenido