Introducción al Método de Monte Carlo
Contenido
import holoviews as hv
hv.extension('bokeh')
import numpy as np
import scipy.stats
3. Introducción al Método de Monte Carlo¶
Los métodos de Monte Carlo son una clase de métodos para resolver problemas matemáticos usando muestras aleatorias (o más bien pseudoaleatorias)
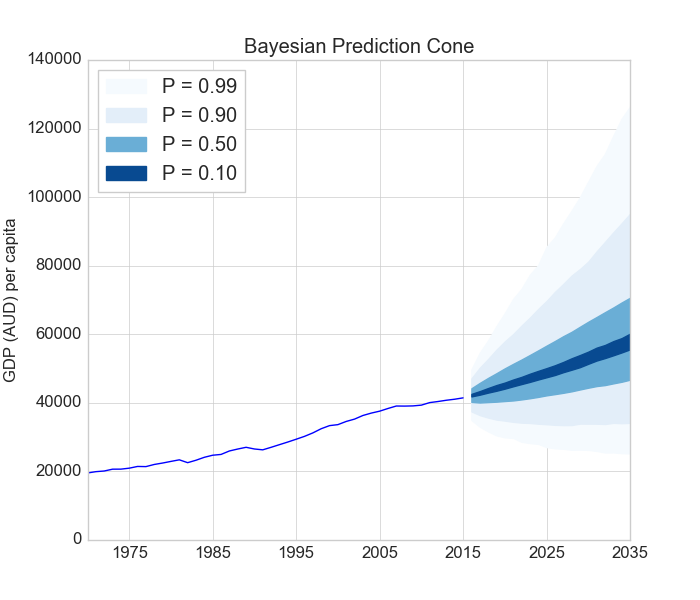
Los métodos de Monte Carlo se usan para predecir el comportamiento de un sistema en un escenario incierto (aleatorio). Por ejemplo en la siguiente figura se predice el valor esperado del Producto Interno Bruto (PIB, GDP en inglés) per capita a un cierto horizonte de tiempo.
Nota
El método de Monte Carlo retorna una distribución de futuros posibles
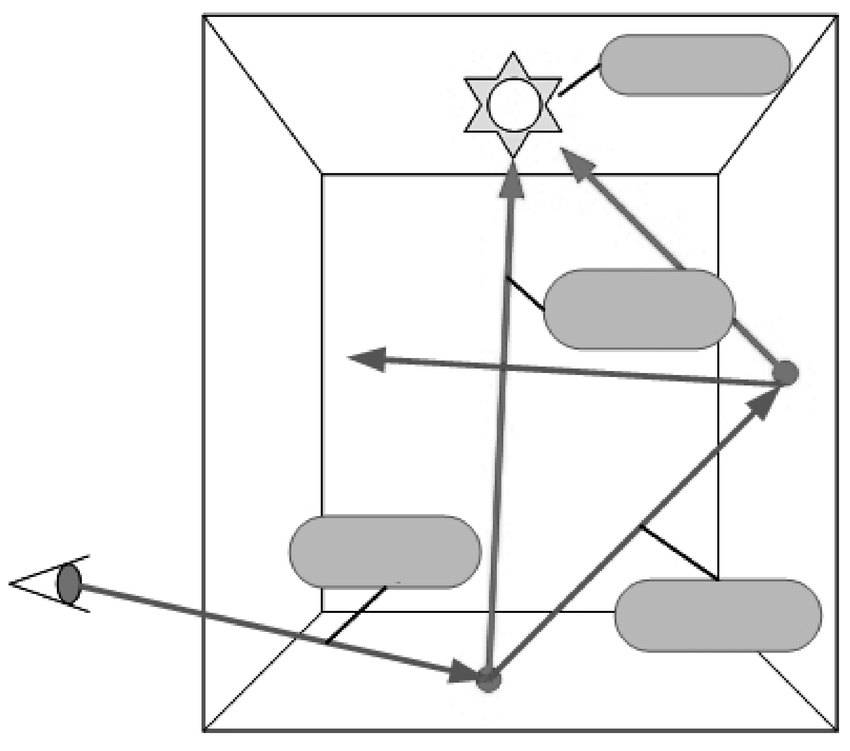
Los métodos de Monte Carlo también pueden usarse en casos completamente determinísticos. Por ejemplo en el problema de estimación de iluminación, la solución analítica puede resultar infactible de calcular.
En lugar de eso se puede aproximar usando una muestra aleatoria de rayos lanzados desde la fuente de iluminación como muestre la siguiente figura. Si lanzamos “suficientes” rayos al azar entonces podemos modelar con bastante exactitud la iluminación real
3.1. Breve nota histórica¶
En los años 40s Stanislaw Ulam, matemático polaco-américano, estaba en cama recuperandose de una enfermedad y pasaba el tiempo jugando solitario. Empezó a interesarse en calcular la probabilidad de ganar el juego de solitario. Trató de desarrollar las combinatorias sin éxito, pues era demasiado complicado.
Luego pensó
Supongamos que juego muchas manos, cuento las veces que gano y divido por la cantidad de manos jugadas
Sin embargo el había jugado muchas manos sin ganar. Posiblemente le tomaría años hacer este conteo.
Ulam pensó entonces en simular el juego usando un computador, por lo que recurrió a John von Neumann, quien implementó el algoritmo propuesto por Ulam en el ENIAC.
Más adelante este algoritmo fue central en las simulaciones realizadas en el proyecto Manhattan. En aquel entonces Nicholas Metropolis, colega de von Neumann y Ulam sugirió el nombre de Monte Carlo, haciendo alusión al famoso casino de Monte Carlo que se encuentra en principado de Monaco en Europa.
3.2. Esquema general de un método de Monte Carlo¶
El método de Monte Carlo es bastante sencillo y puede resumirse en los tres pasos siguientes.
Sea una variable aleatoria \(X\) con distribución \(f(x)\) y una función \(g(x)\)
Se muestrean \(N\) valores de la distribución de \(X\): \(x_i \sim f(x), i=1,\ldots, N\)
Se calcula una “cantidad de interés” en base a los valores muestreados: \(y_i = g(x_i), i=1,\ldots,N\)
Se reduce el resultando usando estadísticos, por ejemplo el promedio de la variable de salida \(\bar y\) o la desviación estándar de la variable de salida \(\sigma_y\)
La cantidad de interés (variable de salida) es también una variable aleatoria. Es conveniente que las variables de entrada sigan una distribución sencilla (e.g. uniforme o normal estándar)
A continuación veremos una aplicación particular del método de Monte Carlo
3.3. Integración por Monte Carlo¶
El valor esperado de una función \(g\) sobre una variable aleatoria \(X\) se define como
donde \(f_X(x)\) es la densidad de probabilidad de \(X\).
Si la función y/o la integral son muy complicadas de calcular analíticamente podemos, en lugar de eso, realizar una “Integración por Monte Carlo”
El algoritmo en este caso es
Muestrar aleatoriamente \(N\) valores \(x_i \sim f_X(x)\)
Evaluar \(y_i = g(x_i)\)
aproximar el valor esperado como
donde \(V = \int f_X(x) \,dx\) es el volumen de integración.
A continuación veremos en acción este método con un ejemplo
3.3.1. Ejemplo: Calculando el valor de \(\pi\)¶
El área es la integral de la función en su dominio
La fórmula analítica del área de un cuadrado de lado \(a\) es \(A_{cuadrado}=a^2\)
La fórmula analítica del área de un circulo de radio \(a\) es \(A_{circulo}=\pi a^2\)
Por lo tanto podemos estimar el valor de \(\pi\) como el cociente entre las dos áreas
En este ejemplo estimaremos el área del circulo utilizando integración por Monte Carlo. Para esto generaremos \(N\) muestras aleatorias en un cuadrado unitario y luego dividiremos las que están “adentro del circulo” por el total.
np.random.seed(12345)
def g(x: np.ndarray) -> bool:
"""
Verificar si la coordenada pertenece o no al círculo
"""
return (x[:, 0] - 0)**2 + (x[:, 1] - 0)**2 - 1. <= 0.
N = 100_000
x = np.random.rand(N, 2) # Nota: El volumen de integración es 1
print(4*np.sum(g(x))/N)
# La multiplicación por cuatro se debe a que estamos considerando un cuarto del circulo.
3.14124
Si bien el resultado no es exactamente \(\pi\) si se aproxima bastante
La siguiente figura muestra graficamente el área de simulación (cuadrado) y las muestras simuladas (puntos negros).
x_plot = np.linspace(0, 1, num=1000)
X1, X2 = np.meshgrid(x_plot, x_plot)
X = np.stack((X1.ravel(), X2.ravel())).T
circle = hv.Image((x_plot, x_plot, g(X).reshape(len(x_plot), len(x_plot))),
kdims=['x[:, 0]', 'x[:, 1]']).opts(cmap='Set1', width=320, height=300)
dots = hv.Points((x[:, 0], x[:, 1])).opts(color='k', size=0.1)
hv.Overlay([circle, dots])
En este momento es interesante preguntar
¿Cómo cambia el resultado si utilizo más o menos muestras aleatorias?
El siguiente gráfico muestra la estimación por Monte Carlo de \(\pi\) en función de \(N\) (línea azul). La línea roja tenue marca el valor real de \(\pi\).
np.random.seed(12345)
logN = np.arange(0, 7, step=0.1)
pi = np.zeros_like(logN)
for i, logn in enumerate(logN):
x = np.random.rand(int(10**logn), 2)
pi[i] = 4.*np.mean(g(x))
plot_estimation = hv.Curve((logN, pi), 'logaritmo de N', 'Estimación de PI').opts(width=500)
plot_real = hv.HLine(np.pi).opts(alpha=0.25, color='r', line_width=4)
(plot_estimation * plot_real)
El siguiente gráfica muestra el error absoluto en escala logarítmica en función de \(N\)
plot_error = hv.Curve((logN, np.abs(pi-np.pi)), 'logaritmo de N', 'Error absoluto').opts(width=500, logy=True)
plot_error
De las figuras podemos notar que
Importante
La estimación por Monte Carlo converge al valor real a medida que \(N\) aumenta
¿En qué crees que se sustenta este resultado? Lo revisaremos a continuación
3.3.2. Propiedades del estimador¶
La distribución asintótica del estimador
es
Importante
El estimador converge a su valor esperado a una tasa de \(\frac{1}{\sqrt{N}}\)
Lo anterior es consecuencia de la Ley Fuerte de los grandes números y del Teorema central del límite
Nota
El estimador converge sin importar cual sea la dimensionalidad de la integral. El método de Monte Carlo es entonces una alternativa interesante para resolver integrales complicadas. Volveremos a este punto más adelante.
3.4. Teoremas clave¶
Ley fuerte de los grandes números
Sean \(X_1, X_2, \ldots, X_N\) variables aleatorias (V.A.) independientes e idénticamente distribuidas (i.i.d.) con
Entonces se cumple que su promedio
cuando \(N \to \infty\). Es decir que el promedio converge al valor esperado con N grande.
Nota
La ley fuerte nos dice que podemos aproximar \(\mu\) con \(\bar X\) pero no nos da pistas sobre que tan cerca está \(\bar X\) de \(\mu\). Esto último es importante puesto que en la práctica \(N\) nunca será \(\infty\)
Teorema central del límite
Si \(X_1, X_2, \ldots, X_N\) son V.A i.i.d., entonces su promedio de distribuye como
cuando \(N \to \infty\). Es decir que cuando N es grande el promedio (suma) se distribuye como una normal centrada en \(\mu\) y con desviación estándar \(\frac{\sigma}{\sqrt{N}}\)
Nota
Lo anterior ocurre sin importar cual sea la distribución original de las V.A., siempre y cuando se cumpla el supuesto i.i.d.
Ejemplo: La distribución promedio de lanzar \(N\) dados
La siguiente gráfica interactiva ejemplifica como el promedio de VAs con distribución multinomial tiende a una distribución normal (y además se concentra) a medida que \(N\) crece
average_dice_histogram = {}
for number_of_dices in [1, 2, 3, 4, 5, 10, 20, 30, 40, 50, 100, 500]:
dist = scipy.stats.multinomial(n=number_of_dices, p=[1/6]*6)
repeats = dist.rvs(size=1000)
average_dice = np.sum(repeats*range(1, 7)/number_of_dices, axis=1)
average_dice_histogram[number_of_dices] = np.histogram(average_dice, bins=80, density=True, range=(1, 6))
hMap = hv.HoloMap(kdims='Número de dados')
for number_of_dices, (bins, edges) in average_dice_histogram.items():
hMap[number_of_dices] = hv.Histogram((edges, bins),
kdims='Promedio de los dados',
vdims='Densidad').opts(width=500)
hMap