8. Teoría de la Información - Parte 1¶

En esta lección veremos:

Cantidad de información y entropía
Codificación de fuente

8.1. Codificación de fuente¶

La codificación de fuente es el proceso que asigna un código a cada símbolo del diccionario

Ejemplo: Queremos codificar las letras del alfabeto (que son 27) usando código binario

Si usamos un código de largo fijo necesitariamos al menos 5 bits: \(2^5 = 32 > 27\)

import string

with open('../data/quijote.txt', 'r') as file:
    texto = file.read()

texto = texto.translate({ord(k): None for k in string.digits})
#texto = texto.lower().encode('ascii', 'ignore').decode("utf-8")
print(f"Largo del texto: {len(texto)} caracteres")
print(f"Cantidad de bits si uso 5 bits por símbolo: {len(texto)*5}")
print(texto[:101] + "...")

Largo del texto: 3029 caracteres
Cantidad de bits si uso 5 bits por símbolo: 15145
En un lugar de la Mancha, de cuyo nombre no quiero acordarme, no ha mucho tiempo que vivía un hidalgo...

Pero algunas letras se ocupan más que otras

El iterador Counter del módulo collections nos permite hacer un histograma de los caracteres

from collections import Counter
Counter(texto).most_common()

[(' ', 540),
 ('a', 316),
 ('e', 312),
 ('o', 201),
 ('s', 189),
 ('n', 160),
 ('l', 160),
 ('r', 151),
 ('d', 123),
 ('u', 112),
 ('i', 110),
 ('c', 99),
 ('t', 88),
 ('m', 60),
 ('b', 45),
 (',', 44),
 ('p', 41),
 ('q', 37),
 ('y', 34),
 ('g', 26),
 ('h', 23),
 ('v', 23),
 ('í', 21),
 ('ó', 16),
 ('z', 14),
 ('f', 13),
 ('j', 11),
 ('.', 9),
 (';', 9),
 ('á', 7),
 ('ñ', 5),
 ('Q', 4),
 ('E', 3),
 (':', 3),
 ('F', 2),
 ('(', 2),
 (')', 2),
 ('é', 2),
 ('\n', 2),
 ('M', 1),
 ('U', 1),
 ('ú', 1),
 ('T', 1),
 ('x', 1),
 ('S', 1),
 ('C', 1),
 ('A', 1),
 ('N', 1),
 ('B', 1)]

Intuición

Podríamos reducir la cantidad de bits si usamos códigos más cortos para las letras más frecuentes

8.2. Introducción a la Teoría de la información¶

La Teoría de la información TI es el estudio matemático sobre la cuantificación y transmisión de la información. Fue propuesto por Claude Shannon en 1948: A Mathematical Theory of Communication.

TI proporciona formas para describir la información de un proceso y tiene importantes aplicaciones en telecomunicaciones, computación y biología (genética). También ha tenido una fuerte influencia en la teoría de codificación y compresión.

Partamos con un ejemplo

Ejemplo: Las dos fuentes

Sean dos fuentes F1 y F2 que pueden emitir uno entre cuatro símbolos: \(A\), \(B\), \(C\) o \(D\)

F1 es completamente aleatoria, es decir: \(P(A) = P(B) = P(C) = P(D) = \frac{1}{4}\)

Si queremos predecir el próximo valor emitido por F1 ¿Cúal es el número mínimo de preguntas con respuesta si/no que debemos hacer?

La respuesta es 2 para cualquiera de los símbolos

F2 en cambio emite \(A\), \(B\), \(C\) y \(D\) con probabilidades \(P(A) =\frac{1}{2}\), \(P(B) =\frac{1}{4}\), \(P(C) = \frac{1}{8}\) y \(P(D) =\frac{1}{8}\), respectivamente

Si queremos predecir el próximo valor retornado por F2 ¿Cúal es el número mínimo de preguntas con respuesta si/no que debemos hacer?

La respuesta es 1 para \(A\), 2 para \(B\) y 3 para \(C\) y \(D\)

8.2.1. Cantidad de información (según Shannon)¶

La cantidad de información de un símbolo \(x\) es el logaritmo en base dos del recíproco de su probabilidad de aparición

\[ I(x) = \log_2 \left(\frac{1}{P(x)} \right) = \log_2 P(x)^{-1} = - \log_2 P(x), \]

que es equivalente a la mínima cantidad de preguntas si/no que debemos hacer para adivinar su valor

La cantidad de información se mide en bits

Un bit es la cantidad de información que se requiere para escoger entre dos alternativas equiprobables

La cantidad de información es también llamada sorpresa

Mientras más improbable es un símbolo, más nos sorprendemos cuando observamos que ocurre

8.2.2. Entropía¶

Sea una variable aleatoria \(X\) (fuente) con \(N\) resultados posibles (símbolos) \(\{x_1, x_2, \ldots, x_N\}\) donde cada símbolo \(x_i\) tiene una probabilidad \(p_i \in [0, 1]\) y \(\sum_{i=1}^N p_i = 1\)

Por ende cada símbolo tiene una cantidad de información \(I(x_i) = -\log_2 \left( p_i \right)\)

Definimos la cantidad de información promedio de \(X\) como

\[\begin{split} \begin{align} H (X) &= \mathbb{E}_{x\sim X} \left [ - \log P(X=x) \right ] \nonumber \\ &= - \sum_{i=1}^N P(X=x_i) \log_2 P(X=x_i) \nonumber \\ &= - \sum_{i=1}^N p_i \log_2 p_i \quad \text{[bits/símbolo]} \nonumber \end{align} \end{split}\]

que se conoce como Entropía de Shannon

Propiedades de la entropía

La entropía es siempre positiva \(H(X) \geq 0\). La igualdad se cumple si un \(x_i\) tiene \(p_i=1\) (caso más predecible)
La entropia está acotada \(H(X) \leq H_0\), donde \(H_0= \log_2(N)\) es la entropia si \(p_i = \frac{1}{N}~ \forall i\) (caso menos predecible)
La redundancia de \(X\) es \(1 - H(X)/H_0\)

Nota

Mientras más predecible es \(X\) menor es su entropía y mayor es su redundancia

Ejemplo: El retorno de las dos fuentes

En promedio, ¿Cuántas preguntas por símbolo hace la fuente F1?

\(1 \frac{1}{4} + 1 \frac{1}{4} + 1 \frac{1}{4} + 1 \frac{1}{4} = 2\) preguntas por símbolo. Su entropía es \(2\) [bits]

En promedio, ¿Cuántas preguntas por símbolo hace la fuente F2?

\(1 \frac{1}{2} + 2 \frac{1}{4} + 3 \frac{1}{8} + 3 \frac{1}{8} = 1.75\) preguntas por símbolo. Su entropía es \(1.75\) [bits]

Si cada fuente retorna un mensaje de 100 símbolos ¿Cúanta información produjo cada una?

F1 produce 200 bits mientras que F2 produce 175 bits

Mientras más predecible menos información se necesita

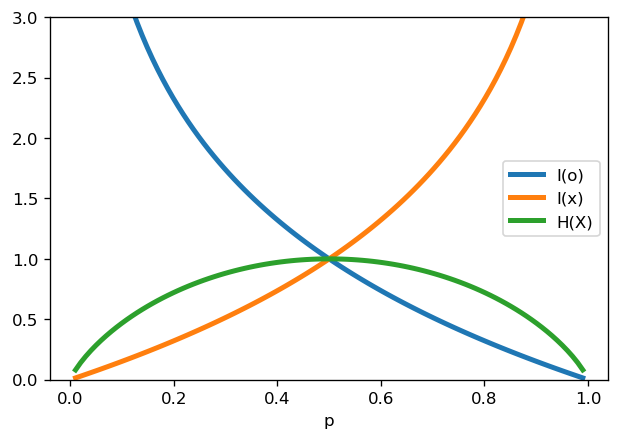
Ejemplo: Moneda con truco

Sea una variable aleatoria \(X\) que modela el resultado de lanzar una moneda y asumamos que el resultado puede tomar solo dos valores: Cara \(o\) o Cruz \(x\)

La probabilidad de que salga cara es \(p_o = p\)
La probabilidad de que salga cruz es \(p_x = 1- p\)

Luego la entropía es

\[\begin{split} \begin{align} H(X) &= -\sum_{i=1}^2 p_i \log_2 p_i \nonumber \\ &= -p_x \log (p_x) - p_o \log p_o \nonumber \\ &= - p \log(p) - (1-p) \log(1-p) \end{align} \end{split}\]

Reflexione:

¿En que casos la entropía es mínima? ¿En qué caso es máxima?
¿Puedes relacionar la entropía con la aleatoridad/sorpresa del resultado de lanzar la moneda?

Ojo: \(\lim_{z\to 0^+} z \log 1/z = 0\)

p = np.linspace(0.01, 0.99, num=100)
H = -p*np.log2(p) - (1-p)*np.log2(1-p)
fig, ax = plt.subplots(1, figsize=(6, 4), sharex=True)
ax.set_xlabel('p')
ax.plot(p, -np.log2(p), label='I(o)', lw=3)
ax.plot(p, -np.log2(1-p), label='I(x)', lw=3)
ax.plot(p, H, label='H(X)', lw=3)
ax.set_ylim([0, 3])
plt.legend();

../../_images/09_codificación_de_fuente_11_0.png

Ejercicio:

Sea una fuente que escupe un entero x que está entre 0 y 31

Considere el resultado de las siguientes preguntas ¿Cúal tiene mayor entropía?

¿Es x igual a 0?
¿Es x un número primo?
¿Es x mayor a 15?

¿Cuál es el número mínimo de preguntas con respuesta si/no que se deben hacer para adivinar el valor de x?

Ejemplo: Meteorólogos del siglo XIX

Nos encontramos a finales del siglo XIX. La estación meteorológica de Niebla hace una predicción del tiempo en Valdivia. Esta información se envía a Valdivia a través de telegrafo. Calcule la cantidad de información promedio que envía la estación a Valdivia en cada escenario usando la entropía de Shannon

Dos posibilidades: Lluvia y nublado, con probabilidad \(1/2\) y \(1/2\), respectivamente
Una posibilidad: Lluvia, con probabilidad \(1\)
Cuatro posibilidades: Lluvia, Nublado, Nubosidad parcial, soleado, con probabilidad \(1/2\), \(1/4\), \(1/8\) y \(1/8\), respectivamente

Respuesta:

Las probabilidades de cada mensaje son \(2^{-1}\), \(2^{-2}\), \(2^{-3}\) y \(2^{-3}\). Luego la cantidad de información de cada mensaje es: 1, 2, 3 y 3 bits, respectivamente. Por ende la entropía es \(1/2 + 1/2 + 3/8 + 3/8 = 1.75\) bits

Pregunta

Para el escenario 3 códifique las alternativas usando un alfabeto de códigos binarios

¿Cómo le asignamos un código a cada alternativa?

Opción 1: Código de ancho fijo

Tenemos cuatro estados.

Si todos los estados tienen igual cantidad de bits, necesitamos 2 bits para representarlos: 00, 01, 10, 11

En este caso resulta equivalente a asumir equiprobabilidad y la entropía es 2 bits

Opción 2: Código de ancho variable (prefijo)

Se usa 1, 2, 3 y 3 bits para cada estado, según su probabilidad de aparición. En este caso la entropía es 1.75 bits

Podemos describir este escenario según

Primera decisión equiprobable: Lluvia (0) vs El resto (1)
Segunda decisión equiprobable: Nublado (10) vs El resto menos lluvia (11)
Tercera decisión equiprobable: Nubosidad parcial (110) vs soleado (111)

Podemos representar graficamente usando un dendograma como se muestra a continuación

Algoritmo de codificación con forma de árbol en base 2
Los mensajes codificados están en las hojas del árbol
Código préfijo: Ningún código puede ser prefijo de otro.
El código prefijo garantiza decodificación sin ambiguedad

Ejercicio

Decodifique la predicción del tiempo para los próximos tres días: 101100

Ejercicio

Si el código de lluvia fuera 1 en lugar de 0, decodifique el siguiente mensaje: 11111

Este es un ejemplo de código ambiguo

Ejemplo: Entropía y cantidad de bits del fragmento del famoso texto

print("Código de largo fijo:", 5*len(texto))
# Código de largo variable:
freq = np.array(list(Counter(texto).values()))
p = freq/np.sum(freq)
print("Código de largo variable:", int(-np.sum(p*np.log2(p))*len(texto)))

Código de largo fijo: 15145
Código de largo variable: 12759

Reflexione:

¿Es la codificación de largo variable lossless o lossy?
En ciertos casos las palabras son más largas de lo que eran originalmente, ¿Cómo comprimimos entonces?

8.3. Codificación de Huffman¶

Un algoritmo sencillo de codificación de tipo prefijo:

Se estima la probabilidad \(p_i\) de cada símbolo
Se ordenan los símbolos en orden descendente según \(p_i\)
Juntar los dos con probabilidad menor en un grupo, su probabilidad se suma
Volver al paso 2 hasta que queden dos grupos
Asignarle 0 y 1 a las ramas izquierda y derecha del árbol, respectivamente
El código resultante se lee desde la raiz hasta la hoja

Debilidad de Huffman:

Códigos con diccionarios/probabilidades variables
En ese caso combiene usar codificación aritmética o Lempel-Ziv

Ejemplo: Codificación de Huffman del famoso texto

Primero estimamos la frecuencia usando collections.Counter

Luego construimos el dendograma usando heapq

Terminamos con un diccionario que transforma cada símbolo del texto en un código

# Implemetación adaptada de https://rosettacode.org/wiki/Huffman_coding#Python
import heapq
# Construir dendograma con las probabilidades ordenadas
dendograma = [[frequencia/len(texto), [simbolo, ""]] for simbolo, frequencia in Counter(texto).items()]
heapq.heapify(dendograma)
# Crear el código
while len(dendograma) > 1:
    lo = heapq.heappop(dendograma)
    hi = heapq.heappop(dendograma)
    for codigo in lo[1:]:
        codigo[1] = '0' + codigo[1]
    for codigo in hi[1:]:
        codigo[1] = '1' + codigo[1]
    heapq.heappush(dendograma, [lo[0] + hi[0]] + lo[1:] + hi[1:])
# Convertir código a diccionario
dendograma = sorted(heapq.heappop(dendograma)[1:])
dendograma = {simbolo : codigo for simbolo, codigo in dendograma} 
display(dendograma)

{'\n': '11011100100',
 ' ': '111',
 '(': '11011100101',
 ')': '11011100110',
 ',': '100010',
 '.': '00010010',
 ':': '0001111110',
 ';': '00010011',
 'A': '110111001110',
 'B': '110111001111',
 'C': '110111010000',
 'E': '0001111111',
 'F': '11011101001',
 'M': '110111010001',
 'N': '110111010100',
 'Q': '1101110110',
 'S': '110111010101',
 'T': '110111010110',
 'U': '110111010111',
 'a': '010',
 'b': '100011',
 'c': '10100',
 'd': '11010',
 'e': '001',
 'f': '10101110',
 'g': '1010110',
 'h': '1010100',
 'i': '11000',
 'j': '00011110',
 'l': '0110',
 'm': '110110',
 'n': '0111',
 'o': '1011',
 'p': '000110',
 'q': '000101',
 'r': '0000',
 's': '1001',
 't': '10000',
 'u': '11001',
 'v': '1010101',
 'x': '110111011100',
 'y': '1101111',
 'z': '10101111',
 'á': '110111000',
 'é': '11011101111',
 'í': '0001110',
 'ñ': '000111110',
 'ó': '0001000',
 'ú': '110111011101'}

Ahora podemos convertir el texto en una tira binaria

texto_codificado = ""
for letra in texto:
    texto_codificado += dendograma[letra]

display(texto_codificado[:1000])

'0001111111011111111001011111101101100110101100100000111110100011110110010111110111010001010011110100101010001010001011111010001111101001100111011111011111011110111101101000110000001111011110111110001011100111000001000010111110101010010110000110100100000110110001100010111011110111111010100010111110110110011010010101001011111100001100000111011000011010111110001011100100111110101011100010101010001110010111110010111111101010011000110100100110101011010111111101000111101101011100111111010001111011001001111010111101011100101111110101001100001100001100110001000010111000101110101101001000001010110010111010011110000110001010110110010101000101110000101110100000111001111111010111001100101010010111111101111111101011001001101010110101111110100101100000000001110101011000000010010111110111010111011101011110110110011001011111010001111010011010101101011111110110110111000100111110101010101010001011100010111001001111101000100000011100100001011100010111100101001100001101100010100000100001111110110010100111'

Podemos usar bytearray para convertir nuestra tira de caracteres 0 y 1 a un arreglo de Bytes

b = bytearray()
for i in range(0, len(texto_codificado), 8): # Si el largo del texto no es múltiplo de 8 debemos hacer padding
    byte = texto_codificado[i:i+8]
    b.append(int(byte, 2))

Guardando el archivo en disco:

with open("../quijote_comprimido.bin", "wb") as f: # Agregamos el diccionario en el header    
    f.write(str(dendograma).encode())
with open("../quijote_comprimido.bin", "a") as f: # salto de linea
    f.write("\n")
with open("../quijote_comprimido.bin", "ab") as f: # Texto codificado
    f.write(bytes(b))
!du -B1 --apparent-size ../quijote*

2446	../quijote_comprimido.bin

En el script quijote_recuperado.py puedes revisar como se descomprime el texto

Hemos visto que las señales pueden tener alta redundancia

Piense por ejemplo en el caso de las imágenes o el lenguaje (contexto)

Hemos visto también como comprimir datos explotando esta redudancia

En particular

Transformamos los datos tal de hacerlos “más independientes”
Opcionalmente los cuantizamos para eliminar información menos importante
Codificamos los datos con una distribución que sea óptima para el canal de transmisión

Este último paso es lo que llamamos codificación de fuente

A continuación revisaremos un importante teorema enunciado por Shannon respecto a la codificación de un mensaje

8.4. Teorema de codificación de fuente de Shannon (Source coding theorem)¶

Dada una variable aleatoria \(X\) con entropía \(H(X)\) existe una codificación de largo variable cuyo largo de palabra promedio \(\bar L\) satisface

\[ H(X) \leq \bar L < H(X) + 1 \]

Es decir que el límite inferior teórico del largo de palabra es \(H(X)\). Esta codificación sin pérdida y de largo variable la llamamos codificación entrópica

Este teorema nos dice cuanto podemos comprimir una señal sin que hayan pérdidas antes de enviarla por un canal (libre de ruido)

También justifica la definición de entropía como medida de la cantidad de información

Otra forma de ver el teorema:

Sea una fuente \(X\) que emite \(N\) mensajes.

Los N mensajes pueden comprimirse en \(N H(X)\) [bits] o más con riesgo de pérdida despreciable (\(N\to\infty\))

Por el contrario

Si comprimimos en menos de \(N H(X)\) [bits] la pérdida está garantizada

Demostración

Sea una codificación C para una variable aleatoria \(X\) con N posibles símbolos

Cada símbolo \(x_i\) tiene una probabilidad de ocurrencia \(p_i \in [0, 1]\) con \(\sum_i p_i = 1\) y un largo de código \(L_i\)

Luego el largo promedio de los códigos es

\[ \bar L = \sum_{i=1}^N p_i L_i \]

¿Qué valores de \(L_i\) resultan en el menor \(\bar L\)?

El largo óptimo es \(L_i^* = -\log_2 p_i\) y el promedio sería \(\bar L^* = H(X)\)

Digamos que proponemos otro largo \(\hat L_i = - \log_2 q_i\), asumiendo que \(\sum_i q_i = 1\)

Luego el largo promedio sería

\[\begin{split} \begin{align} \bar L &= \sum_{i=1}^N p_i \hat L_i = - \sum_{i=1}^N p_i \log_2 q_i \nonumber \\ &= - \sum_{i=1}^N p_i \log_2 q_i - \sum_{i=1}^N p_i \log_2 p_i + \sum_{i=1}^N p_i \log_2 p_i \nonumber \\ &= - \sum_{i=1}^N p_i \log_2 p_i + \sum_{i=1}^N p_i \log_2 \frac{p_i}{q_i} \nonumber \\ &= H(X) + \sum_{i=1}^N p_i \log_2 \frac{p_i}{q_i} \geq H(X) \nonumber \end{align} \end{split}\]

Con esto probamos que no hay mejor largo que \(-\log_2 p_i\)

Notemos que los \(L_i^*\) no tendrían porque ser un número enteros

Nota

En general la codificación óptima cumple: \(H(X) \leq \bar L^* < H(X) + 1\)

Se puede estar entre esas cotas con el algoritmo de Huffman
La codificación aritmética en cambio casi siempre llega a la cota inferior
La codificación de Huffman y aritmética son codificaciones entrópicas

8.5. Algoritmos de compresión para video¶

En la lección anterior vimos el algoritmo JPEG para compresión de imágenes

En esta lección hemos visto la codificación de Huffmann. Con este hemos visto todos los pasos necesarios para implementar el algoritmo JPEG

Consideremos ahora el caso en que tenemos un stream de video (sin audio) y queremos transmitirlo comprimido

Un algoritmo clásico es Motion-JPEG el cual se basa en el algoritmo JPEG que ya hemos visto. Tiene dos variantes

La primera denominada intraframe consiste en aplicar el algoritmo JPEG a cada cuadro como si fueran imágenes independientes. Es un algoritmo simple pero ingenuo ya que no está tomando en cuenta que existe mucha correlación entre cuadros
La segunda denominada interframe consiste en aplicar el algoritmo JPEG a las diferencias entre cuadros. Si los movimientos son lentos las diferencias entre cuadros serán pequeñas y la codificación entrópica podrá reducir mucho más el tamaño. En general se codifica un cuadro completo denominado keyframe y luego una cierta cantidad de diferencias entre el keyframe y los cuadros siguientes.

Esta idea es la que está detrás de algoritmos más modernos como MPEG

MPEG es un estándar de codificación para video de tipo inter-frame

Explota la redundancia entre los bloques de 8x8 de un cuadro y su sucesor

Existen tres tipos de cuador/frame en MPEG-1

I: Se comprime el frame completo con JPEG. Se envía una frame I cada N frames
P: Se predicen las diferencias con respecto al frame I o P anterior.
B: Se calculan diferencias en base al frame I o P más cercano anterior y posterior

INFO239 Comunicaciones

Teoría de la Información - Parte 1

Contenido