3. Análisis de Señales¶

En esta lección veremos

Covarianza, correlación y convolución
Transformada de Fourier discreta
Transformada rápida de Fourier

3.1. Notación¶

Función de tiempo continuo: \(g(t)\)
Función de tiempo discreto: \(g[n] = g(t_n)\) con \(t_n = n T_s, n\in [0, N]\)
Tiempo o intervalo de muestreo: \(T_s\)

En la siguiente figura se muestra una señal de tiempo continuo (linea gris) muestreada a tiempo regular (flechas rojas)

3.2. Comparando señales en el tiempo¶

Covarianza y correlación cruzada

Podemos analizar la similitud entre dos señales \(g(\cdot)\) y \(f(\cdot)\) en función de un retardo \(\tau\) usando el la covarianza cruzada

\[ \text{COV}_{gf}(\tau) = \mathbb{E}[(g(t)-\mu_g)(f(t + \tau)-\mu_f)], \]

y para procesos discretos con retardo \(m\):

\[ \text{COV}_{gf}[m] = \frac{1}{N} \sum_{n=1}^N (g[n] - \bar g)(f[n+m] - \bar f), \]

donde la media de la señal se estima como \( \bar g = \frac{1}{N} \sum_{n=1}^N g[n]\).

Si las señales tienen distinta escala es conveniente usar la correlación cruzada

\[ \rho_{gf}[m] = \frac{\text{COV}_{gf}[m]}{\hat \sigma_g \hat \sigma_f}, \]

donde la desviación estándar de la señal se estima como \(\hat \sigma_g = \frac{1}{N} \sqrt{\sum_{n=1}^N (g[n] - \bar g)^2}\)

Nota

Podemos calcular la covarianza entre dos señales usando la función np.correlate de NumPy

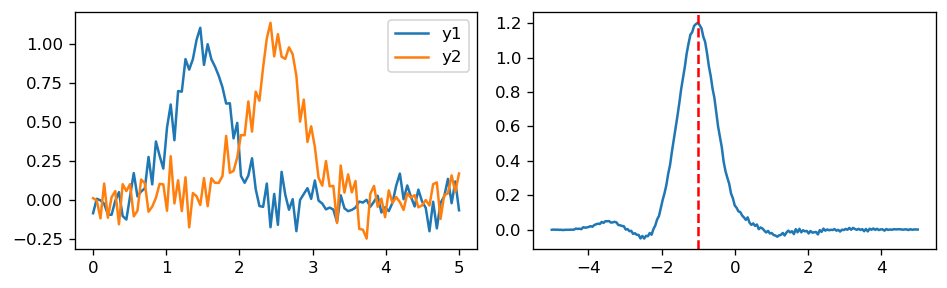
Ejemplo

Usando la correlación para encontrar el desfase o desplazamiento temporal relativo entre dos señales

x = np.linspace(0.0, 5.0, num=100)
y1 = np.exp(-4.0*(x-1.5)**2) + 0.1*np.random.randn(len(x))
y2 = np.exp(-4.0*(x-2.5)**2) + 0.1*np.random.randn(len(x))
tau = np.linspace(-x[-1], x[-1], 2*len(x)-1)
crosscorr = np.correlate(y1, y2, mode='full')/(len(x)*np.std(y1)*np.std(y2))

fig, ax = plt.subplots(1, 2, figsize=(8, 2.5), tight_layout=True)
ax[0].plot(x, y1, label='y1')
ax[0].plot(x, y2, label='y2')
ax[0].legend()
ax[1].plot(tau, crosscorr);
idx_max = np.argmax(crosscorr)
display(f"y1 está separado por {tau[idx_max]:0.4f} segundos de y2")
ax[1].axvline(tau[idx_max], c='r', ls='--');

'y1 está separado por -1.0101 segundos de y2'

../../_images/03_análisis_de_señales_5_1.png

Autocorrelación

También es de interés comparar una señal consigo misma usando la autocorrelación

\[ \rho_{gg}[m] = \frac{\text{COV}_{gg}[m]}{\hat \sigma_g^2}= \frac{1}{(N-m) \hat \sigma_g^2} \sum_{n=1}^{N-m} (g[n] - \bar g)(g[n+m] - \bar g), \]

Esto nos permite analizar en que momento \(m\) la señal se parece más a si misma: periodicidad

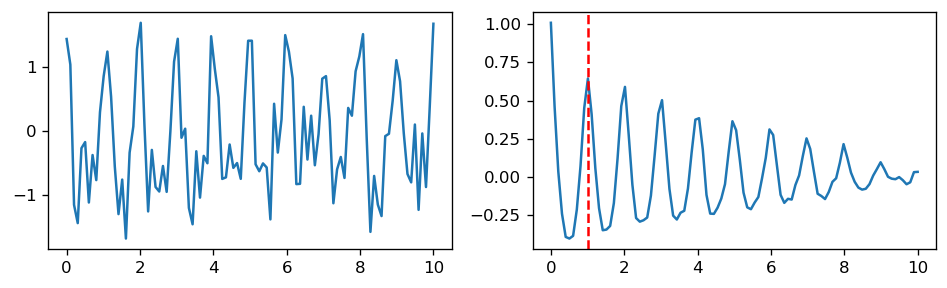
Ejemplo

El período de la señal corresponde al segundo máximo de la autocorrelación

x = np.linspace(0.0, 10.0, num=100)
y = np.cos(2.0*np.pi*1*x) + 0.5*np.cos(2.0*np.pi*2*x) + 0.5*np.random.randn(len(x))

tau = np.linspace(0, x[-1], len(x))
autocorr = np.correlate(y, y, mode='full')[len(x)-1:]/(len(x)*np.var(y))

fig, ax = plt.subplots(1, 2, figsize=(8, 2.5), tight_layout=True)
ax[0].plot(x, y)
ax[1].plot(tau, autocorr)
ax[1].axvline(tau[1+np.argmax(autocorr[1:])], c='r', ls='--')
display(f"El periodo (frecuencia fundamental de la señal es {tau[1+np.argmax(autocorr[1:])]:0.4f} segundos")

'El periodo (frecuencia fundamental de la señal es 1.0101 segundos'

../../_images/03_análisis_de_señales_8_1.png

Convolución

La operación de producto punto entre versiones desplazadas de funciones se llama convolución y se denota con \(*\)

\[ (f*g) (\tau) = \int g(t) f(\tau - t) \,dt = \int f(t) g(\tau - t) \,dt \]

La convolución discreta se define como

\[ (f*g)[m] = \sum_n f[n] g[n-m] \]

las funciónes de covarianza y correlación se pueden escribir como convoluciones

Nota

Podemos realizar la convolución usando la función np.convolve de NumPy

Ejemplo

Convolución entre una señal cuadrada (naranja) y una Gaussiana (azul)

El resultado es una versión con bordes suavizados de la señal cuadrada (derecha)

fig, ax = plt.subplots(1, 2, figsize=(8, 2.5), tight_layout=True)

t = np.arange(-4, 4, step=1e-2)

def gaussian(t, a=0, s=0.2):
    return np.exp(-np.absolute(t-a)**2/s**2)

def square(t, a=0, T=1):
    s = np.zeros(shape=(len(t),))
    s[np.absolute(t-a) < T] = 1
    return s

conv_s = np.convolve(gaussian(t), square(t), mode='same')
ax[0].plot(t, gaussian(t))
ax[0].plot(t, square(t))
ax[1].plot(t, conv_s);

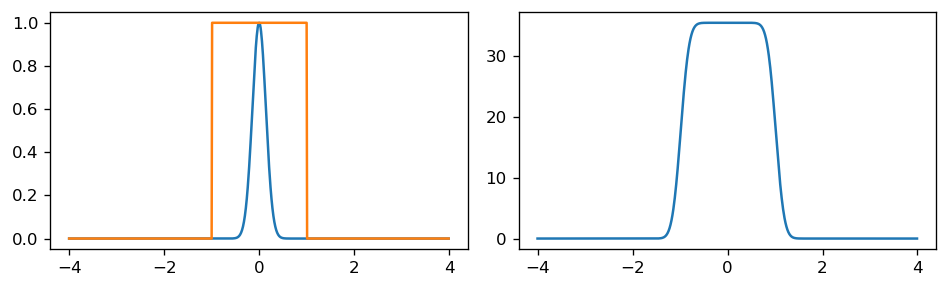
../../_images/03_análisis_de_señales_11_0.png

La siguiente animación muestra una representación gráfica de la convolución

El resultado de la convolución (derecha) es la integración del area que se marca en celeste en la figura de la izquierda

%%capture 
fig, ax = plt.subplots(1, 2, figsize=(8, 2.5), tight_layout=True)

def update(a = 0): 
    ax[0].cla(); ax[1].cla()
    p1, p2 = gaussian(t, 0.1*a - 4), square(t)
    ax[0].plot(t, p2); ax[0].plot(t, p1); 
    ax[0].fill_between(t, 0, p1*p2, alpha=0.5)
    ax[1].plot(t, conv_s[::-1]); ax[1].scatter(0.1*a -4, np.sum(p1*p2), s=100, c='k')
    return ()
    
anim = animation.FuncAnimation(fig, update, frames=80, interval=100, blit=True)

HTML(anim.to_html5_video())

3.3. Análisis en frecuencia: Transformada de Fourier¶

Una herramienta de gran relevancia para el análisis de señales es la Transformada de Fourier

La transformada de Fourier de una señal \(g(t)\) se define como

\[\begin{split} \begin{align} G(f) &= \mathcal{F}[g(t)] = \int_{-\infty}^{\infty} g(t) \exp(-j2\pi f t) \,dt \\ &= \int_{-\infty}^{\infty} g(t) \cos(2\pi f t) \,dt - j \int_{-\infty}^{\infty} g(t) \sin(2\pi f t) \,dt \end{align} \end{split}\]

donde

Usamos el operador \(\mathcal{F}\) para denotar la transformada
Tipicamente se usa \(G\) para la transformación de \(g\)
\(G\) es ahora una función de la frecuencia

Usando la transformada de Fourier podemos analizar las frecuencias de oscilación predominantes de una señal

def matrix_DFT(signal):
    N = len(signal)
    W_N = np.exp(-1j*2*np.pi/N)
    n = np.arange(N)
    Omega = W_N**(n*n.reshape(1,-1).T)
    S = np.dot(Omega, signal)
    return np.dot(Omega, signal)

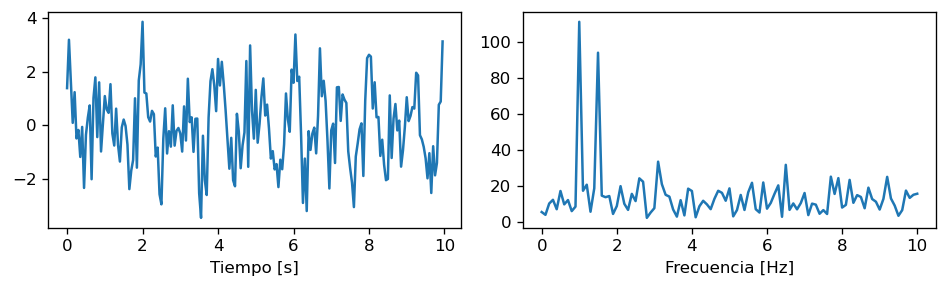
Fs = 20
t = np.arange(0.0, 10.0, step=1/Fs)
g = np.cos(2.0*np.pi*1*t) + np.cos(2.0*np.pi*1.5*t) + 1.0*np.random.randn(len(t))
f = np.linspace(0, Fs/2, num=len(t)//2+1)
Gabs = np.abs(matrix_DFT(g))

fig, ax = plt.subplots(1, 2, figsize=(8, 2.5), tight_layout=True)
ax[0].plot(t, g)
ax[0].set_xlabel("Tiempo [s]")
ax[1].plot(f, Gabs[:len(f)])
ax[1].set_xlabel("Frecuencia [Hz]");
display(f"Las frecuencias predominantes son: {f[Gabs[:len(f)] > 50]} [Hz]")

'Las frecuencias predominantes son: [1.  1.5] [Hz]'

../../_images/03_análisis_de_señales_16_1.png

Representación en coordenadas polares

Es usual descomponer la transformada de Fourier en el espectro de amplitud y el espectro de fase

\[ G(f) = |G(f)| \exp({j\varphi(f)}) \]

Donde

\(|G(f)|\) es el espectro de amplitud
\(\varphi(f)\) es el espectro de fase (ángulo)

Propiedad: La transformada de Fourier es invertible

\[\begin{split} \begin{align} g(t) &= \mathcal{F}^{-1}[G(f)] =\int_{-\infty}^{\infty} G(f) \exp(j2\pi f t) \,df \\ &= \int_{-\infty}^{\infty} G(f) \cos(2\pi f t) \,df + j \int_{-\infty}^{\infty} G(f) \sin(2\pi f t) \,df \end{align} \end{split}\]

Propiedad: La convolución en el tiempo se convierte en multiplicación en frecuencia y viceverza (Lathi & Ding, 2009, Sec 3.3.6)

\[ \mathcal{F}[g(t)*y(t)] = \mathcal{F}[g(t)] \mathcal{F}[y(t)] = G(f) Y(f) \]

Propiedad: La transformada de Fourier es un operador lineal

\[\begin{split} \begin{align} \mathcal{F}[a g_1(t) + b g_2(t) ] &= a\mathcal{F}[g_1(t)] + b \mathcal{F}[g_2(t) ] \\ &= a G_1(f) + b G_2(f) \end{align} \end{split}\]

Teorema: (de) Parseval:

La energía de una señal se preserva. La transformada de Fourier no pierde información. (Lathi & Ding, 2009, Sec 3.7.1)

\[ \int_{-\infty}^{\infty} |g(t)|^2 \,dt = \int_{-\infty}^{\infty} |G(f)|^2 \,df \]

Teorema: (de) Wiener-Khinchin:

La transformada de Fourier de la autocorrelación es la densidad espectral de potencia y viceverza (Lathi & Ding, 2009, 3.7.5)

\[ |G(f)|^2 = \int_{-\infty}^{\infty} \rho_{gg}(\tau) \exp({-j2\pi f \tau }) \,dt = \mathcal{F}[\rho_{gg}(\tau)] \]

\[ \rho_{gg}(\tau) = \int_{-\infty}^{\infty} |G(f)|^2 \exp({j2\pi\tau f}) \,df = \mathcal{F}^{-1}[|G(f)|^2] \]

La densidad espectral es la potencia asignada a cada frecuencia de la señal

3.3.1. Transformada de Fourier discreta (DFT)¶

Para computar la transformada de Fourier sobre señales muestreadas (discretas) usamos la DFT

El resultado es una transformada de Fourier definida en un conjunto discreto de frecuencias

Sea una señal discreta \(g[n]\) con \(n \in [0, N-1]\) y tiempo de muestreo \(T_s\), es decir \(t[n] = n T_s\)

La DFT se define como

\[ G[k] = \sum_{n=0}^{N-1} g[n] \exp \left(-j2\pi f[k] t[n] \right) = \sum_{n=0}^{N-1} g[n] \exp \left( -j 2\pi \frac{k n}{N} \right) , \]

donde

\(f[k] = k f_0 ~~ \forall k \in [-\frac{(N-1)}{2}, \frac{(N-1)}{2}]\)
\(f_0 = \frac{F_s}{N}\)
\(F_s = \frac{1}{T_s}\)
\(t[n] = n T_s\)

La DFT es también invertible

\[ g[n] = \frac{1}{N} \sum_{k=0}^{N-1} G[k] \exp \left( j2\pi \frac{k n}{N} \right) \]

Notar que N puntos en el tiempo se mapean con N frecuencias independientes

Para tener una notación más clara definiremos

\[ W_N = \exp \left( -j \frac{2\pi}{N} \right) \]

Luego podemos escribrir la DFT como

\[ G[k] = \sum_{n=0}^{N-1} g[n] W_N^{kn} \]

Podemos escribir el sistema de ecuaciones

\[ G[k] = \sum_{n=0}^{N-1} g[n] W_N^{kn} \]

en forma matricial como

\[\begin{split} \begin{align} \begin{pmatrix} G[0] \\ G[1] \\ G[2] \\ \vdots \\ G[N-1] \\ \end{pmatrix} &= \begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & W_N & W_N^2 & \cdots & W_N^{N-1} \\ 1 & W_N^2 & W_N^4 & \cdots & W_N^{N-2} \\ \vdots & \dots & \dots & \ddots & \vdots \\ 1 & W_N^{N-1} & W_N^{N-2} & \cdots & W_N \\ \end{pmatrix} \begin{pmatrix} g[0] \\ g[1] \\ g[2] \\ \vdots \\ g[N-1] \\ \end{pmatrix} \nonumber \\ G &= \Omega g, \end{align} \end{split}\]

que corresponde a \(N\) tiempos definidos como

\[ t = 0, ~ T_s, ~2 T_s , ~3 T_s, \ldots, ~(N-1) T_s \]

y a \(N\) frecuencias definidas como

\[ f = -\frac{F_s}{2}, \ldots, 0, ~\frac{F_s}{N}, ~2 \frac{F_s}{N} , ~3 \frac{F_s}{N}, \ldots, ~\frac{F_s}{2} \]

En el ejemplo anterior implementamos la DFT como una multiplicación matricial usando Numpy

Multiplicación entre una matriz de NxN y un vector de Nx1
N sumas de N multiplicaciones, complejidad cuadrática

def matrix_DFT(signal):
    N = len(signal)
    W_N = np.exp(-1j*2*np.pi/N)
    n = np.arange(N)
    Omega = W_N**(n*n.reshape(1,-1).T)
    S = np.dot(Omega, signal)
    return S

3.3.2. Transformada rápida de Fourier o FFT¶

La computación de la DFT tiene complejidad \(\mathcal{O}(N^2)\)

Nota

Existen varios algoritmos exactos con complejidad \(\mathcal{O}(N\log N)\) para calcular la DFT: La Fast Fourier Transform (FFT)

El algoritmo de FFT más conocido es el de Cooley-Tukey, en donde se obtiene una FFT recursiva que explota las periodicidades en la matriz \(\Omega\)

\[\begin{split} \begin{align} G[k] &= \sum_{n=0}^{N-1} g_n \exp \left(-j2\pi \frac{k n}{N} \right) \\ &= \sum_{n=0}^{N/2-1} g_{2n} \exp \left(-j2\pi \frac{k 2n}{N} \right) + \sum_{n=0}^{N/2-1} g_{2n+1} \exp \left(-j2\pi \frac{k (2n+1)}{N} \right) \\ &= \sum_{n=0}^{N/2-1} g_{2n} \exp \left(-j2\pi \frac{k n}{N/2} \right) + \exp \left(-j2\pi \frac{k}{N} \right) \sum_{k=0}^{N/2-1} g_{2n+1} \exp \left(-j2\pi \frac{k n}{N/2} \right) \\ &= G_E[k] + \exp \left( -j2\pi \frac{k}{N} \right) G_O[k] ~~ \forall k \in [0,N/2] \end{align} \end{split}\]

Notar que se calculan dos “medias” DFT

Para continuar usaremos la siguiente propiedad de la exponencial compleja

\[ \exp \left(-j2\pi \frac{k+ N/2}{N}\right) = \exp \left(-j2\pi \frac{k}{N} \right) \exp \left(-j\pi\right) = - \exp \left(-j2\pi \frac{k}{N} \right) \]

Además por periodicidad/simetría de la DFT

\[\begin{split} \begin{align} G_E[k + N/2] &= \sum_{n=0}^{N/2-1} g_{2n} \exp \left( -j2\pi \frac{(k+ N/2)n}{N/2} \right) \\ &= \sum_{n=0}^{N/2-1} g_{2n} \exp \left(-j2\pi \frac{k n}{N/2} \right) \exp \left(-j2\pi n \right) = G_E[k] \end{align} \end{split}\]

Finalmente

\[\begin{split} \begin{align} G[k] &= G_E[k] + \exp \left( -j2\pi \frac{k}{N} \right) G_O[k] ~~~ \forall k \in [0,N/2] \\ G[k + N/2] &= G_E[k + N/2] - \exp \left( -j2\pi \frac{k}{N} \right) G_O[k + N/2] \\ &= G_E[k] - \exp \left( -j2\pi \frac{k}{N} \right) G_O[k] \\ \end{align} \end{split}\]

En resumen

Para obtener \(G[k]\) y \(G[k + N/2]\):

Calculamos \(G_E[k]\) y \( \exp \left( -j2\pi \frac{k}{N} \right) G_O[k]\)
Sumamos o restamos los términos, respectivamente

Es decir que reducimos los cálculos necesarios a la mitad

Ejemplo

Sea una señal aleatoria con dias muestras

Calculemos y comparemos la DFT de los pares (puntos naranjos) e impares (cruces azules)

t = np.linspace(0, 10, num=10)
x = np.random.randn(len(t))
plt.figure(figsize=(6, 2), tight_layout=True)
plt.plot(t, x, c='k', alpha=0.5)
plt.scatter(t[::2], x[::2], marker='x', zorder=100)
plt.scatter(t[1::2], x[1::2], marker='o', zorder=100);

../../_images/03_análisis_de_señales_25_0.png

La función np.close retorna True si todos los elementos de los arreglos tienen una diferencia menor a 1e-8

np.set_printoptions(precision=3)
N = len(x)
W_N = np.exp(-1j*2*np.pi/N)

S = matrix_DFT(x)
Se = matrix_DFT(x[0::2]) # Transformada de Fourier de los pares
So = matrix_DFT(x[1::2]) # Transformada de Fourier de los impares
display(S[:N//2], Se + W_N**np.arange(N//2)*So)
display(np.allclose(S[:N//2], Se + W_N**np.arange(N//2)*So))
display(S[N//2:], Se - W_N**np.arange(N//2)*So)
display(np.allclose(S[N//2:], Se - W_N**np.arange(N//2)*So))

array([-0.964+0.j   , -1.52 -4.137j,  0.653-1.628j, -2.13 -3.092j,
       -0.658+0.476j])

array([-0.964+0.j   , -1.52 -4.137j,  0.653-1.628j, -2.13 -3.092j,
       -0.658+0.476j])

True

array([ 4.277+5.022e-16j, -0.658-4.760e-01j, -2.13 +3.092e+00j,
        0.653+1.628e+00j, -1.52 +4.137e+00j])

array([ 4.277+0.j   , -0.658-0.476j, -2.13 +3.092j,  0.653+1.628j,
       -1.52 +4.137j])

True

El algoritmo FFT continua dividiendo en pares hasta llegar a \(N\log N\) productos, como muestra la siguiente figura

3.4. Implementaciones de la FFT¶

Python: numpy.fft y scipy.fft
C: The Fastest Fourier Transform in the WEst (FFTW)
OpenCV: Enfocado en señales bidimensionales (lo veremos más adelante)

En lo que sigue usaremos:

Funciones principales

Para obtener la transformada de Fourier usando el modulo fft de scipy usamos

fft.fft y fft.ifft: Calcula la transformada y la transformada inversa (caso general)
fft.rfft y fft.irfft: Calcula la transformada y la transformada inversa para señales con valores reales
fft.fftfreq y fft.rfftfreq: Crea una arreglo de frecuencias consistente con las funciones anteriores

import scipy.fft

Ejemplo: Comparación entre implementación matricial usando NumPy y FFT de scipy

Primero creamos una serie de tiempo con frecuencia de muestreo \(F_s\)

Fs = 20
t = np.arange(0.0, 10.0, step=1/Fs)
g = np.cos(2.0*np.pi*1*t) + np.cos(2.0*np.pi*1.5*t) + 1.0*np.random.randn(len(t))
fig, ax = plt.subplots(figsize=(8, 2.5), tight_layout=True)
ax.plot(t, g);

../../_images/03_análisis_de_señales_33_0.png

Para calcular la FFT usamos

G = scipy.fft.rfft(g)
display(G[:10])

array([  4.658 +0.j   ,  11.17  -6.519j, -16.456-26.884j,   6.762 -7.148j,
        -9.299-12.139j,  11.051 -1.596j, -12.692 +2.41j ,  -4.455 -5.758j,
        -8.252 -2.95j ,   5.264 +6.864j])

La FFT es imaginaria, podemos recuperar

el espectro de magnitud usando la función np.abs
el espectro de fase usando np.angle

Para generar el vector de frecuencias asociado a la FFT usamos

freq = scipy.fft.rfftfreq(n=len(g), d=1/Fs)
display(freq[:10])

array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])

Finalmente dibujamos los espectros de magnitud

fig, ax = plt.subplots(figsize=(8, 2.5), tight_layout=True)
ax.plot(freq, np.abs(matrix_DFT(g))[:len(freq)], label='Numpy matmul', alpha=.75, lw=2)
ax.plot(freq, 
        np.abs(scipy.fft.rfft(g)), label='fftpack', alpha=.75, lw=2, ls='dashed')
ax.set_xlabel("Frecuencia [Hz]")
plt.legend(loc=1);

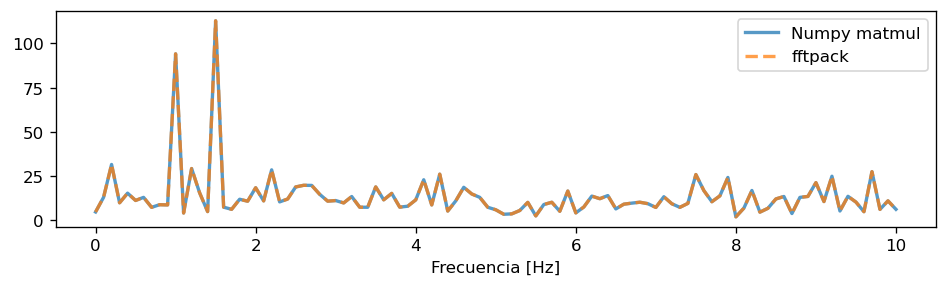
../../_images/03_análisis_de_señales_39_0.png

y comparamos los tiempos de cómputo

¿Cuántos órdenes de magnitud más rápido es la FFT?

%timeit -n 10 np.abs(matrix_DFT(g))
%timeit -n 10 np.abs(scipy.fft.fft(g))

36.7 ms ± 4.16 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
57.1 µs ± 24.7 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

INFO239 Comunicaciones

Análisis de Señales

Contenido

3. Análisis de Señales¶

3.1. Notación¶

3.2. Comparando señales en el tiempo¶

3.3. Análisis en frecuencia: Transformada de Fourier¶

3.3.1. Transformada de Fourier discreta (DFT)¶

3.3.2. Transformada rápida de Fourier o FFT¶

3.4. Implementaciones de la FFT¶