from IPython.display import YouTubeVideo
from functools import partial
YTVideo_formato = partial(YouTubeVideo, width=640, height=400, rel=0, modestbranding=1)
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import scipy.fft
import cv2
from PIL import Image
5. Análisis de imágenes en frecuencia#
En esta lección veremos:
Transformada de Fourier bidimensional
Espectro de imágenes sintéticas y naturales
5.1. Transformada de Fourier bidimensional#
La DFT se puede aplicar a funciones multi-dimensionales
En el caso discreto de una señal bidimensional \(g[n_1, n_2]\) con índices \(n_1 \in [0, N_1-1]\) y \(n_2 \in [0, N_2-1]\) tenemos
y su inversa
Notemos que
Es decir que la DFT 2D se puede calcular usando repetidas veces la DFT de una dimensión.
Ejemplo: Visualización de la base de Fourier bidimensional
A continuación se muestra la base de Fourier (parte real), son cosenos en dos dimensiones con distintas orientaciones
La frecuencia cero se ubica en la esquina superior izquierda
La frecuencia crece de izquierda a derecha y de arriba para abajo
Cuando aplicamos la transformada de Fourier 2D a una imagen estamos separando la imagen en base a estas “texturas” sinusoidales
x = np.arange(0, 32, step=1)
X, Y = np.meshgrid(x, x)
fig, ax = plt.subplots(9, 9, figsize=(6, 6), tight_layout=True)
for n in range(9):
for m in range(9):
ax[n, m].matshow(np.cos(2.0*np.pi*X*m/len(x) + 2.0*np.pi*Y*n/len(x)),
cmap=plt.cm.RdBu_r, vmin=-1, vmax=1)
ax[n, m].axis('off')

5.2. Espectro de una imagen#
Podemos usar la transformada de Fourier 2D para obtener el espectro de amplitud de una imagen
Utilizaremos la siguiente imagen como ejemplo
valdivia = cv2.imread('data/valdivia.jpg')
valdivia_bw = cv2.cvtColor(valdivia, cv2.COLOR_BGR2GRAY)[:, 300:]
Image.fromarray(valdivia_bw)

OpenCV tiene implementada la transformada rápida de Fourier en 2 dimensiones
La función dft de opencv nos retorna una tensor con dos canales que contienen la parte real y la parte imaginaria de la transformada. Luego podemos utilizar magnitude para obtener el espectro
valdivia_bw_float = np.float32(valdivia_bw)
valdivia_dft = cv2.dft(valdivia_bw_float, flags=cv2.DFT_COMPLEX_OUTPUT)
valdivia_magnitude = cv2.magnitude(valdivia_dft[:,:,0], valdivia_dft[:,:,1])
Si lo graficamos directamente veremos:
fig, ax = plt.subplots(figsize=(8, 5))
ax.pcolor(valdivia_magnitude, cmap=plt.cm.Greys_r);
Que sigue la convención usual, es decir que la frecuencia cero está en la esquina.
Podemos hacer una visualización más clara dejando el cero al centro con:
fig, ax = plt.subplots(figsize=(8, 5))
x_axis = scipy.fft.fftshift(scipy.fft.fftfreq(valdivia_magnitude.shape[1]))
y_axis = scipy.fft.fftshift(scipy.fft.fftfreq(valdivia_magnitude.shape[0]))
ax.pcolor(x_axis, y_axis, scipy.fft.fftshift(valdivia_magnitude), cmap=plt.cm.Greys_r);

Nota
La energía está muy concentrada en el componente central. Esto es común en imágenes naturales
Para visualizar mejor el espectro de una imagen natural se recomienda usar
de esta forma el componente central no es tan dominante. En este caso:
fig, ax = plt.subplots(figsize=(8, 5))
ax.pcolor(x_axis, y_axis,
scipy.fft.fftshift(np.log(valdivia_magnitude+1)), cmap=plt.cm.Greys_r);

Ahora podemos apreciar otras estructuras en el espectro, pero
Atención
¿A qué corresponden?
Para entrenarnos en la interpretación del espectro conviene estudiar espectros de imágenes sintéticas
5.3. Espectro de una imagen sintética#
Ejemplo: Impulsos en frecuencia
Dos impulsos en el espectro corresponde a una sinusoide en el espacio original y viceversa
La posición de los impulsos está asociada a la frecuencia de la sinusoide
YTVideo_formato('JkYpoMWGbN4')
Ejemplo: Espectro de una Linea
Una línea en la imagen es una línea en el espectro (con otra orientación)
YTVideo_formato('vwey-8_EADg')
Atención
¿Cómo se explica esto?
Consideremos primero el caso donde la rotación es 40 pixeles (linea vertical)
fig, ax = plt.subplots(1, 2, figsize=(8, 4), tight_layout=True);
def draw_line_spectrum(ax, angle):
img = np.zeros(shape=(80, 80));
for i in range(80):
img[i, int(i - 2*angle*i/80 + angle)] = 1
ax[1].set_title("Espectro de magnitud");
ax[0].set_title("Imagen")
S_img = np.abs(scipy.fft.fft2(img))
im = ax[1].imshow(scipy.fft.fftshift(S_img), cmap=plt.cm.Greys_r,
extent=[-40, 40, 40, -40])
im = ax[0].imshow(img, cmap=plt.cm.Greys_r);
draw_line_spectrum(ax, 40)

Notemos que en este caso la componente vertical y horizontal pueden independizarse como muestra el sencillo ejemplo a continuación
A = np.array([[0., 0., 1., 0., 0.]])
B = np.array([[1., 1., 1., 1., 1.]])
A*B.T
array([[0., 0., 1., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 1., 0., 0.]])
Esto se conoce como una señal separable
Propiedad: La DFT 2D de una señal separable equivale a la multiplicación de las dos DFT 1D
Una señal es sepable si
luego aplicando esto en la DFT tenemos
es decir que se obtiene la multiplicación de cada DFT.
Usemos esta propiedad en el ejemplo anterior.
La primera señal es un impulso en el origen. Su transformada de Fourier es una señal constante
SA = scipy.fft.fftshift(np.abs(scipy.fft.fft(A)))
display(A, SA)
array([[0., 0., 1., 0., 0.]])
array([[1., 1., 1., 1., 1.]])
La segunda señal es una constante
Su transformada de Fourier es un impulso en el origen
(la constante y el impulso en el origen son un par de Fourier)
SB = scipy.fft.fftshift(np.abs(scipy.fft.fft(B)))
display(B, SB)
array([[1., 1., 1., 1., 1.]])
array([[0., 0., 5., 0., 0.]])
Resultado: La multiplicación de ambas es una linea rotada en 90 grados con respecto a la original
SA*SB.T
array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[5., 5., 5., 5., 5.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
Atención
¿Por qué pareciera repetirse la linea en el espectro cuando la rotación es distinta de 0 pixeles (0 grados), 40 pixeles (90 grados) o 80 pixeles (180 grados)?
fig, ax = plt.subplots(1, 2, figsize=(8, 4), tight_layout=True);
draw_line_spectrum(ax, 50)

Este efecto o artefacto obedece a la siguiente propiedad de la DFT
Propiedad: La DFT es periodica
En este caso el artefacto que observamos se debe a que en ciertos ángulos los bordes no calzan, tal como muestra la siguiente figura
fig, ax = plt.subplots(figsize=(8, 4), tight_layout=True);
img = np.zeros(shape=(80, 80));
for i in range(80):
img[i, int(i - 2*50*i/80 + 50)] = 1
S_img = scipy.fft.fftshift(np.abs(scipy.fft.fft2(img)))
ax.imshow(np.tile(S_img, (3,3)), plt.cm.Greys_r)
ax.axhline(80, c='r', ls='--')
ax.axhline(160, c='r', ls='--')
ax.axvline(80, c='r', ls='--')
ax.axvline(160, c='r', ls='--');
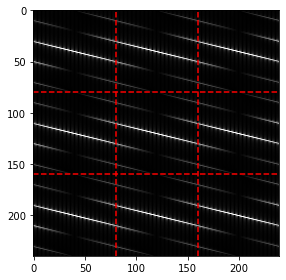
Más adelante veremos como disminuir la influencia de este artefacto usando enventanado
Ejemplo: Espectro de un rectangulo
Un rectangulo en la imagen es un sinc en el espectro (y viceverza)
Notemos como mientras más ancho es el rectangulo más angosto es el sinc (y viceversa)
Demostración para una dimensión: https://www.thefouriertransform.com/pairs/box.php
YTVideo_formato('4ctVzvU89lw')
Ejemplo: Espectro de una Gaussiana
Una Gaussiana en el espectro es una Gaussiana en el espacio de la imagen
Sin embargo el ancho de la gaussiana en el espectro es inversamente proporcional a la del espacio de la imagen
Demostración para una dimensión: https://www.thefouriertransform.com/pairs/gaussian.php
YTVideo_formato('2Sukn_-4Wss')
Ejemplo: Espectro de ruido blanco
El espectro de una imagen de ruido blanco es también ruido blanco
El adjetivo “blanco” se refiere a que es un ruido sin color, es decir que aparece de igual forma en todas las frecuencias de la señal
El video a continuación muestre imágenes de ruido blanco gaussiano generado con distitnas semillas y sus correspondientes espectros de magnitud
YTVideo_formato("mUTdCJzxLkc")
5.4. Espectro de magnitud y de fase#
La DFT en dos dimensiones \(G[k_1, k_2]\) es un número complejo y como tal puede escribirse en coordenadas polares como
donde \(j\) es el número imaginario.
Hasta ahora solo hemos estudiando el valor absoluto \(M = | G |\), esto es lo que se conoce como espectro de magnitud
La magnitud espectral guarda información de la amplitud de los componentes de frecuencia en la imagen
Ahora estudiaremos la influencia que tiene \(\Phi[k_1, k_2]\), es decir el espectro de fase o ángulo
La fase espectral guarda información de la ubicación de los componentes de frecuencia en la imagen
Consideremos la siguiente imagen de ejemplo
doge = cv2.cvtColor(cv2.imread('data/doge.jpg'), cv2.COLOR_BGR2GRAY)
Image.fromarray(doge)

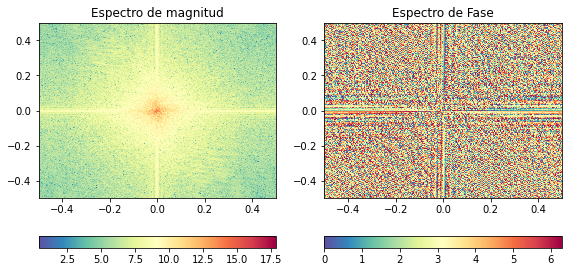
¿Cómo se ven los espectros de magnitud y fase de esta imagen?
doge_dft = cv2.dft(np.float32(doge), flags=cv2.DFT_COMPLEX_OUTPUT)
doge_magnitude, doge_phase = cv2.cartToPolar(doge_dft[:,:,0], doge_dft[:,:,1])
fig, ax = plt.subplots(1, 2, figsize=(8, 4), tight_layout=True)
x_axis = scipy.fft.fftshift(scipy.fft.fftfreq(doge_dft.shape[1]))
y_axis = scipy.fft.fftshift(scipy.fft.fftfreq(doge_dft.shape[0]))
im = ax[0].pcolor(x_axis, y_axis, scipy.fft.fftshift(np.log(1.+doge_magnitude)), cmap=plt.cm.Spectral_r)
ax[0].set_title('Espectro de magnitud')
fig.colorbar(im, ax=ax[0], orientation='horizontal')
ax[1].set_title('Espectro de Fase')
im = ax[1].pcolor(x_axis, y_axis, scipy.fft.fftshift(doge_phase), cmap=plt.cm.Spectral_r)
fig.colorbar(im, ax=ax[1], orientation='horizontal');
Atención
¿Podemos reconstruir la imagen usando sólo el espectro de magnitud? ¿O usando sólo el de fase?
Con este sencillo experimento podemos resaltar que es lo que guarda cada espectro
def reconstruct(mag, phase):
return cv2.dft(cv2.merge([*cv2.polarToCart(mag, phase)]),
flags=cv2.DFT_INVERSE | cv2.DFT_REAL_OUTPUT | cv2.DFT_SCALE)
def hist_eq(img, nbins=256):
image_hist, bins = np.histogram(img.flatten(), nbins, density=True)
cdf = image_hist.cumsum()
cdf = 255 * cdf / cdf[-1]
image_eq = np.interp(img.flatten(), bins[:-1], cdf)
return image_eq.reshape(img.shape).astype('int')
#return img
fig, ax = plt.subplots(2, 2, figsize=(8, 6), tight_layout=True)
for ax_ in ax.ravel():
ax_.axis('off')
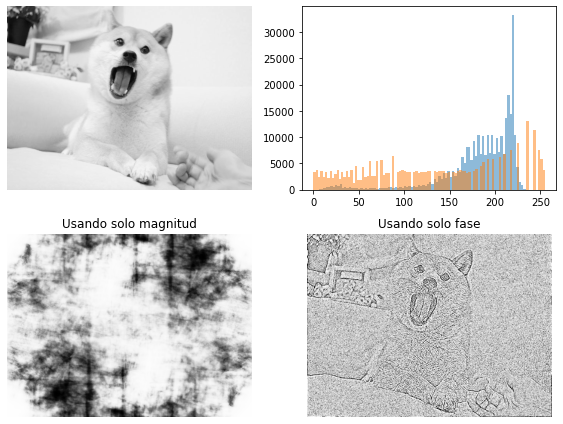
ax[0, 0].imshow(doge, cmap=plt.cm.Greys_r);
ax[0, 1].hist(doge.ravel(), alpha=0.5, bins=100);
ax[0, 1].hist(hist_eq(doge.ravel()), alpha=0.5, bins=100);
ax[0, 1].axis('on')
ax[1, 0].set_title('Usando solo magnitud')
ax[1, 0].imshow(hist_eq(reconstruct(doge_magnitude, np.zeros_like(doge_magnitude))), cmap=plt.cm.Greys_r);
ax[1, 1].set_title('Usando solo fase')
ax[1, 1].imshow(hist_eq(reconstruct(np.ones_like(doge_phase), doge_phase)), cmap=plt.cm.Greys_r);
La base de Fourier representa las texturas presentes en la imagen
El espectro de amplitud nos dice la importancia de cada textura
El espectro de fase nos dice la dirección de cada textura
Si solo usamos la importancia sin la dirección el resultado es ininteligible
Si solo usamos sólo la dirección podemos entender los contornos pero se pierden la información de intensidad de color (importancia)
Atención
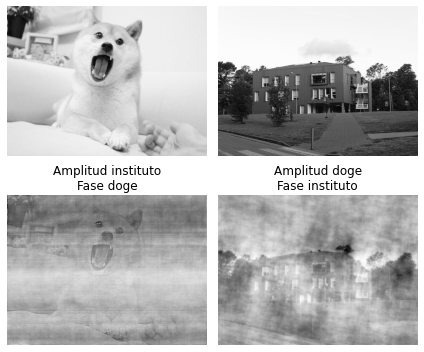
¿Qué pasa si intercambiamos la fase y magnitud de dos imágenes de igual tamaño?
inst = cv2.cvtColor(cv2.imread('data/InsInformatica.jpg'), cv2.COLOR_BGR2GRAY)
inst_dft = cv2.dft(np.float32(inst), flags=cv2.DFT_COMPLEX_OUTPUT)
inst_magnitude, inst_phase = cv2.cartToPolar(inst_dft[:,:,0], inst_dft[:,:,1])
fig, ax = plt.subplots(2, 2, figsize=(6, 5), tight_layout=True)
for ax_ in ax.ravel():
ax_.axis('off')
ax[0, 0].imshow(doge, cmap=plt.cm.Greys_r);
ax[0, 1].imshow(inst, cmap=plt.cm.Greys_r);
ax[1, 0].set_title('Amplitud instituto\nFase doge')
ax[1, 0].imshow(reconstruct(inst_magnitude, doge_phase), cmap=plt.cm.Greys_r);
ax[1, 1].set_title('Amplitud doge\nFase instituto')
ax[1, 1].imshow(reconstruct(doge_magnitude, inst_phase), cmap=plt.cm.Greys_r);