Aplicación: Visualización de espacio latente de estrellas variables
Contenido
Aplicación: Visualización de espacio latente de estrellas variables¶
Datos¶
Existen muchos tipos de objeto astronómico cuyo brillo varía en el tiempo. Una herramienta fundamental para estudiar estos objetos son las curvas de luz.
Una curva de luz es una serie de tiempo del brillo aparente de un objeto astronómico.
El brillo aparente o flujo se estima a partir de las imágenes de telescopio utilizando técnicas de fotometría. Un mismo objeto es “seguido” por varias noches como muestra el siguiente esquema:

|

|
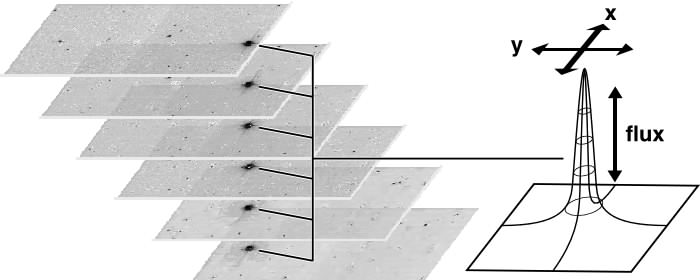
La colección de mediciones para un mismo objeto se grafica en el tiempo como muestra el siguiente ejemplo:
import sys
import holoviews as hv
hv.extension('bokeh')
sys.path.append('../src/')
from preprocessing import load_ztf_data
from plotting import plot_light_curve
lcs, periods, labels = load_ztf_data()
plot_light_curve(lcs[0])
donde:
El eje horizontal corresponde al tiempo, que se expresa en días julianos.
El eje vertical corresponde a la magnitud, una medida relativa de brillo aparente (menor magnitud, más brillante).
Las barras de error corresponden al error fotométrico, un estimado de la calidad de la medición.
El color representa al filtro óptico utilizado. En este caso se utilizaron dos filtros.
De la figura también podemos apreciar las características típicas de una curva de luz:
Irregularmente muestreadas: El tiempo entre observaciones no es constante.
Multivariadas: Una serie de tiempo por filtro, observadas de forma no simultanea.
Heteroscedástica: La varianza del ruido cambia en el tiempo:.
Estrellas variables periódicas
Las curvas de luz son particularmente útiles para estudiar las estrellas variables.
Las estrellas variables son estrellas cuyo brillo varía en el tiempo ya sea de forma regular o estocástica.
Un ejemplo de variabilidad regular son las estrellas pulsantes como las RR Lyrae y las Cefeidas.
from IPython.display import YouTubeVideo
YouTubeVideo('sXJBrRmHPj8')
Estas estrellas pulsan radialmente y de forma regular, se expanden (calientan) y contraen (enfrían) con un periódo estable.
Si conocemos el período \(P\) de la estrella se puede utilizar la siguiente transformación (epoch folding):
para convertir el eje de tiempo en un eje de fase, como muestra el siguiente esquema:
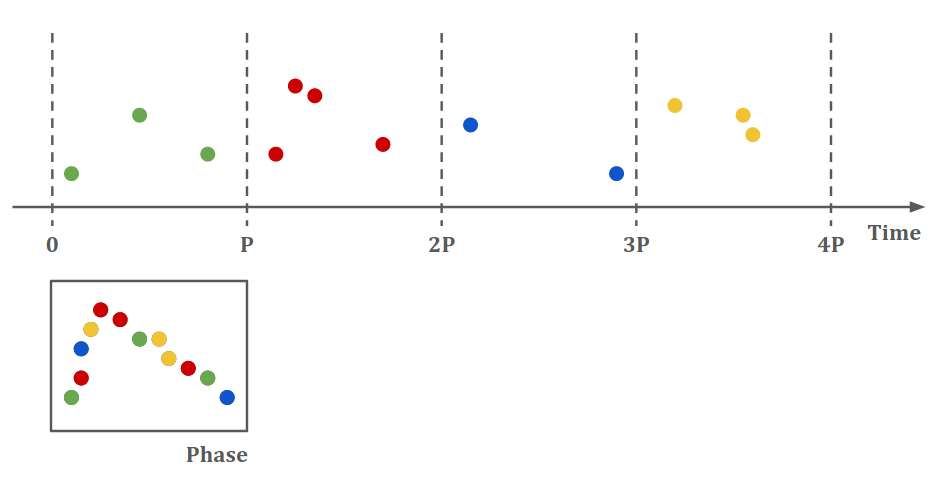
Por ejemplo, la curva de luz que se mostró anteriormente tiene un periodo de:
periods[0]
0.6692088
dias, y si lo utilizamos para “doblar” tenemos:
data_plot = plot_light_curve(lcs[0], periods[0])
data_plot
La curva “doblada” representa de forma clara lo que ocurren durante una fase de la periodicidad de la estrella
Para entrenar un modelo sobre las curvas dobladas primero las interpolaremos a una grilla regular mediante suavizado por kernel.
El resultado del suavizado para la curva anterior se muestra a continuación:
import numpy as np
from preprocessing import kernel_smoothing
from plotting import plot_smoothed
pha_interp = np.linspace(0, 1, num=40)
mag_interp, err_interp, _ = kernel_smoothing(lcs[0], periods[0], pha_interp, align=False, normalize=False)
data_plot * plot_smoothed(pha_interp, mag_interp, err_interp)
Modelo¶
En este ejemplo práctico utilizaremos un AutoEncoder Variacional (Variational Autoencoder, VAE) (Kingma et al., 2014) para reducir la dimensionalidad de un dataset de curvas de luz de estrellas variables.
El siguiente es un diagrama del modelo:
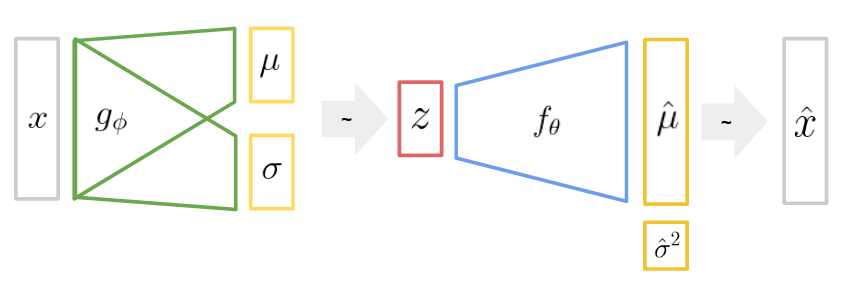
donde
\(x\) se refiere a los datos observados, en este caso las curvas de luz.
\(z\) se refiere a la variable latente de dimensión reducida que queremos inferir.
\(g_\phi\) es una red neuronal artificial que llamaremos Codificador.
\(f_\theta\) es una red neuronal artificial que llamaremos Decodificador.
Un VAE es un modelo probabilístico generativo donde se consideran los siguientes supuestos:
\(p(z) = \mathcal{N}(0, I)\), es decir la distribución a priori de \(z\) es normal estándar.
\(p(x|z) = \mathcal{N}(\hat \mu, \hat \sigma^2)\), una verosimilitud normal para \(x\).
Se utiliza el decodificador para modelar \(\hat \mu = f_\theta(z)\).
Lo que buscamos es inferir \(z\) a partir de \(x\), es decir el posterior de \(z\):
Como lo anterior es muy difícil de calcular lo reemplazamos por una aproximación variacional. En este caso el posterior variacional es una distribución normal multivariada con covarianza diagonal (sin correlaciones):
donde el codificador se utiliza para modelar \(\mu_i, \sigma_i = g_\phi(x_i)\) de forma amortizada. Además se utiliza el truco de reparametrización (segunda linea de la ecuación).
Implementación¶
Implementaremos un VAE para curvas de luz de estrellas periódicas con dos bandas utilizando en flax, considerando lo siguiente:
El codificador procesa cada banda por separado y luego las combina en un único espacio latente.
El codificador retorna la media y la desviación estándar de la variable latente.
La desviación estándar debe ser no-negativa.
El decodificador recibe la variable latente y genera las curvas de cada banda.
from typing import Sequence, Callable
import jax
import jax.numpy as jnp
import flax.linen as nn
class Encoder(nn.Module):
hidden_units: int
latent_dim: int
activation: Callable = nn.relu
@nn.compact
def __call__(self, x):
g_0 = self.activation(nn.Dense(self.hidden_units)(x[:, 0, :])) # g-band
g_1 = self.activation(nn.Dense(self.hidden_units)(x[:, 1, :])) # r-band
g = self.activation(nn.Dense(self.hidden_units*2)(jnp.concatenate([g_0, g_1], axis=1)))
g = self.activation(nn.Dense(self.hidden_units)(g))
z_loc = nn.Dense(self.latent_dim)(g)
z_scale = nn.softplus(nn.Dense(self.latent_dim)(g))
return z_loc, z_scale
class Decoder(nn.Module):
output_dim: int
hidden_units: int
activation: Callable = nn.relu
@nn.compact
def __call__(self, z):
f = self.activation(nn.Dense(self.hidden_units)(z))
f = self.activation(nn.Dense(self.hidden_units*2)(f))
f_loc0 = self.activation(nn.Dense(self.output_dim)(f))
f_loc1 = self.activation(nn.Dense(self.output_dim)(f))
x_loc0 = nn.Dense(self.output_dim)(f_loc0) # g-band
x_loc1 = nn.Dense(self.output_dim)(f_loc1) # r-band
return x_loc0, x_loc1
Por conveniencia implementaremos también un módulo que llame a los anteriores y realice el truco re-parametrización del espacio latente:
class VAE(nn.Module):
hidden_units: int
latent_dim: int
output_dim: int
@nn.compact
def __call__(self, x, z_rng_key):
z_loc, z_scale = Encoder(self.hidden_units, self.latent_dim)(x)
eps = random.normal(z_rng_key, z_scale.shape)
z = z_loc + eps*z_scale
x_loc0, x_loc1 = Decoder(self.output_dim, self.hidden_units)(z)
return x_loc0, x_loc1, z_loc, z_scale
Preparación de datos¶
A continuación se preparan los datos para entrenar el modelo.
El modelo se entrena sobre curvas en fase (dobladas) que han sido interpoladas a una grilla regular mediante suavizado con kernels.
Se aplica un reescalamiento de tipo MinMax a las curvas interpoladas.
Las curvas en fase se alinean para partir en el mínimo de magnitud (máximo brillo)
import sys
import numpy as np
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
labels_int = le.fit_transform(labels)
pha_interp = np.linspace(0, 1, num=40)
mag_interp = np.zeros(shape=(len(lcs), 2, len(pha_interp)))
err_interp = np.zeros(shape=(len(lcs), 2, len(pha_interp)))
for k, (lc, period) in enumerate(zip(lcs, periods)):
mag_interp[k], err_interp[k], _ = kernel_smoothing(lc, period, pha_interp)
mags_interp_jax = jnp.array(mag_interp)
errs_interp_jax = jnp.array(err_interp)
WARNING:jax._src.lib.xla_bridge:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
Entrenamiento¶
Para entrenar el modelo utilizaremos el algoritmo de optimización AMSgrad, que es una extensión de gradiente descedente con tasa de aprendizaje adaptiva (Adam).
A continuación se muestra la función chain de la librería optax la cual permite implementar optimizadores customizados. En este caso el optimizador primero satura las gradientes con norma mayor a 10.0, luego aplica escala los gradients con las reglas adaptivas de AMSgrad y finalmente multiplica por la tasa de aprendizaje inicial:
import optax
optimizer = optax.chain(optax.clip_by_global_norm(10.0),
optax.scale_by_amsgrad(),
optax.scale(-1e-3))
Luego implementaremos la función de costo de VAE, el Evidence Lower Bound (ELBO) de la aproximación variacional. Matemáticamente esto se define como
donde, bajo los supuestos considerados, el término de la mano derecha tiene la siguiente solución analítica:
Para optimizar el VAE se busca maximizar el ELBO en función de los parámetros del codificador y decodificador.
Utilizaremos compilación JIT para acelerar el cálculo de los gradientes del ELBO
def negELBO(params, mag, err, key):
x_loc0, x_loc1, z_loc, z_scale = model.apply(params, mag, key)
d0 = 0.5*jnp.sum(jnp.square((x_loc0 - mag[:, 0, :])/err[:, 0, :]), axis=-1)
d1 = 0.5*jnp.sum(jnp.square((x_loc1 - mag[:, 1, :])/err[:, 1, :]), axis=-1)
kl_div = 0.5 * jnp.sum(-1 - 2*jnp.log(z_scale) + jnp.square(z_loc) + jnp.square(z_scale), axis=-1)
return jnp.sum(d0 + d1 + kl_div)
grad_loss_jit = jax.jit(jax.value_and_grad(negELBO, argnums=0))
Finalmente inicializamos el modelo y el optimizador y lanzamos la rutina de entrenamiento.
Se entrena por 300 épocas con minibatches de tamaño 32:
import jax.random as random
from tqdm import tqdm
from train_utils import data_loader
key = random.PRNGKey(12345)
model = VAE(output_dim=40, hidden_units=100, latent_dim=2)
key, key_ = random.split(key)
params = model.init(key, jnp.zeros(shape=(1, 2, 40)), key_)
state = optimizer.init(params)
loss_history = []
for epoch in tqdm(range(300)):
loss_epoch = 0.0
key, key_ = random.split(key)
for bmag, berr in data_loader(key_, mags_interp_jax, errs_interp_jax,
batch_size=32, shuffle=True):
key, key_ = random.split(key)
loss_val, grads = grad_loss_jit(params, bmag, berr, key_)
loss_epoch += loss_val.item()
updates, state = optimizer.update(grads, state, params)
params = optax.apply_updates(params, updates)
loss_history.append(loss_epoch/len(lcs))
hv.Curve(loss_history, 'Epoch', 'negative ELBO').opts(width=500, logy=True)
100%|████████| 300/300 [18:57<00:00, 3.79s/it]
Evaluación y visualizaciones¶
Primero utilizamos el modelo para inferir las reconstrucciones y variables latentes del dataset completo:
key, key_ = random.split(key)
x_loc0, x_loc1, z_loc, z_scale = model.apply(params, mag_interp, key_)
A continuación se muestra ejemplos de distintos tipos de estrella variable. Las lineas corresponden a las reconstrucciones del modelo y las datos de entrada (curvas de luz interpoladas).
from plotting import plot_reconstruction, plot_latent_space, plot_latent_generation
hv.Layout([plot_reconstruction(x_loc0[idx], x_loc1[idx], pha_interp,
mag_interp[idx], err_interp[idx], labels[idx]) for idx in [0, 2000, 3550, 3385]]).cols(2)
Luego se visualiza el espacio latente bidimensional. Cada color representa un tipo de estrella variable.
Podemos notar que las clases tienden a separarse en el espacio latente. Notar que el entrenamiento fue no supervisado, la clase no se utilizó para ajustar el modelo.
plot_latent_space(z_loc, z_scale, labels_int, le)
VAE es un modelo generativo. Podemos aprovechar esta capacidad para interpolar en el espacio latente y visualizar las formas de curva de luz que el modelo aprendió a reconstruir.
from functools import partial
z1 = jnp.linspace(-1, 1, 9)
z2 = jnp.linspace(-2, 2, 9)
decoder = Decoder(model.output_dim, model.hidden_units)
generate_lc = partial(jax.jit(decoder.apply), {'params': params['params']['Decoder_0']})
plot_latent_generation(z1, z2, pha_interp, generate_lc)
Comentarios:
La reducción no-lineal de dimensionalidad nos permite hacer visualizaciones y explorar un dataset cuando no se tienen etiquetas. También puede utilizarse en estrategias de aprendizaje activo (active learning) para etiquetar un dataset de forma eficiente.
El espacio latente puede utilizarse también como entrada a un clasificador si se cuenta con algunas etiquetas (semi-supervisado).
La capacidad generativa del modelo puede aprovecharse para hacer aumentación de datos y también para interpretar lo que ha aprendido el modelo durante el entrenamiento.